京都大学 理系 2015年度 第2問 解説
問題編
【問題】
次の2つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ。(a) 少なくとも2つの内角は90°である。
(b) 半径1の円が内接する。ただし、円が四角形に内接するとは、円が四角形の4つの辺すべてに接することをいう。
【考え方】
まぁ、見た感じ「正方形が答えだろ」っていうことしか思わないわけですが。
四角形の面積を直接求めるのは難しそうです。しかし、円の中心と接点とを結ぶ線で四角形を切っていくと、面積を求めることができるようになります。
抽象的で取り組みにくい問題ですが、前提条件がかなり厳しいので自由度はそんなに高くありません。四角形の内角が決まると面積も決まる、ということを利用すれば、すっきりと計算できます。
解答編
【問題】
次の2つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ。(a) 少なくとも2つの内角は90°である。
(b) 半径1の円が内接する。ただし、円が四角形に内接するとは、円が四角形の4つの辺すべてに接することをいう。
【解答】
四角形ABCDが条件を満たすとする。内接する円の中心をOとする。また、AB, BC, CD, DAが円と接する点をそれぞれ、P, Q, R, Sとおく。
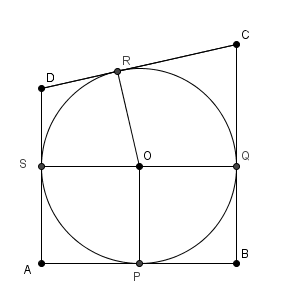
四角形ABCDの面積は、4つの四角形APOS, BQOP, CROQ, DSORの和である。
四角形APOSに注目すると、OP=OS=1であり、$\angle$OPA=$\angle$OSA=90°である(特に、このことから$\angle$Aは180°未満であることがわかる)。よって、AP=$\displaystyle \frac{1}{\tan\frac{\angle A}{2} }$なので、四角形APOSの面積は、$\displaystyle 2\cdot \frac{1}{2}AP\cdot OP=\frac{1}{\tan\frac{\angle A}{2} }$となる。
同様にすると、四角形ABCDの面積は、
\begin{eqnarray}
\frac{1}{\tan\frac{\angle A}{2} }
+\frac{1}{\tan\frac{\angle B}{2} }
+\frac{1}{\tan\frac{\angle C}{2} }
+\frac{1}{\tan\frac{\angle D}{2} }
\end{eqnarray}となる。
すべての内角が90°だった場合は、上の式から面積は4となる。そうでない場合、90°でない内角を$\theta$、$\pi-\theta$と書く($0\lt \theta \lt \pi$)。条件から、残りの2つの内角は90°である。よって面積は
\begin{eqnarray}
& &
\frac{1}{ \tan\frac{\theta}{2} }
+\frac{1}{ \tan\frac{\pi - \theta}{2} }
+2 \\[5pt]
&=&
\frac{1}{\tan\frac{\theta}{2} }
+\tan\frac{\theta}{2}
+2 \\[5pt]
&\geqq&
2\sqrt { \frac{1}{\tan\frac{\theta}{2} }
\tan\frac{\theta}{2} }
+2
=4
\end{eqnarray}
となる(相加相乗平均の関係を用いた)。等号成立は、$\frac{1}{\tan\frac{\theta}{2} }=\tan\frac{\theta}{2}$のとき、つまり、$\tan\frac{\theta}{2}=1$なので、$\theta$が90°のとき。今、90°でない場合を考えているので、等号は成り立たない。
以上のことから、面積が最小になるのはすべての内角が90°のときで、その時の面積は4である。
【解答終】
【解説】
4つの角度のうち、隣り合う角が90°の場合と向かい合う角が90°になる場合でわけてもいいですが、基本的に両方とも同じような議論になります。上の解答からもわかるとおり、分割してできる4つの四角形の面積は、もとの四角形の内角にのみ依存しています。なので、隣の角がどうなっていようが関係はなく、場合分けをする必要もありません。





