京都大学 文系 2022年度 第2問 解説
問題編
問題
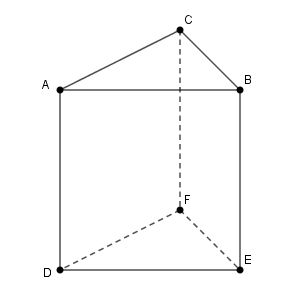
下図の三角柱 ABC-DEF において、 A を始点として、辺に沿って頂点を $n$ 回移動する。すなわち、この移動経路\[ \mathrm{ P }_0 \to \mathrm{ P }_1 \to \mathrm{ P }_2 \to \cdots \to \mathrm{ P }_{n-1} \to \mathrm{ P }_n \](ただし $\mathrm{ P }_0=\mathrm{ A }$)において、 $\mathrm{ P }_0\mathrm{ P }_1$, $\mathrm{ P }_1\mathrm{ P }_2$, $\cdots$, $\mathrm{ P }_{n-1}\mathrm{ P }_n$ はすべて辺であるとする。また、同じ頂点を何度通ってもよいものとする。このような移動経路で、終点 $\mathrm{ P }_n$ が A, B, C のいずれかとなるものの総数 $a_n$ を求めよ。
考え方
動き方はわかりやすいので、状況を理解するのは簡単でしょう。確率漸化式の問題をやったことがあれば、似たような方法で考えることができます。
解答編
問題
下図の三角柱 ABC-DEF において、 A を始点として、辺に沿って頂点を $n$ 回移動する。すなわち、この移動経路\[ \mathrm{ P }_0 \to \mathrm{ P }_1 \to \mathrm{ P }_2 \to \cdots \to \mathrm{ P }_{n-1} \to \mathrm{ P }_n \](ただし $\mathrm{ P }_0=\mathrm{ A }$)において、 $\mathrm{ P }_0\mathrm{ P }_1$, $\mathrm{ P }_1\mathrm{ P }_2$, $\cdots$, $\mathrm{ P }_{n-1}\mathrm{ P }_n$ はすべて辺であるとする。また、同じ頂点を何度通ってもよいものとする。このような移動経路で、終点 $\mathrm{ P }_n$ が A, B, C のいずれかとなるものの総数 $a_n$ を求めよ。
解答
$\mathrm{ P }_n$ が D, E, F のいずれかになるものの総数を $b_n$ とする。
A からは、 B, C, D のどれかに移動できるので、 $a_1=2$, $b_1=1$ である。
また、今、 A, B, C のどれかにいる場合、次も A, B, C のどれかにいる移動の方法は2通り、 D, E, F のどれかに移動する方法は1通りある。今 D, E, F にいる場合も同様に考えると、次の2つの式が成り立つ。
\begin{eqnarray}
a_{n+1} &=& 2a_n+b_n \\[5pt]
b_{n+1} &=& a_n+2b_n \\[5pt]
\end{eqnarray}ここで、辺々加えると\[ a_{n+1}+b_{n+1}=3(a_n+b_n) \]となり、数列 $\{a_n+b_n\}$ は初項が $3$ で公比が $3$ の等比数列だとわかるので\[ a_n+b_n=3^n \]となることがわかる。また、辺々引くと\[
a_{n+1}-b_{n+1}=a_n-b_n \]となり、 $a_1-b_1=1$ で一定であることがわかる。よって\[ a_n-b_n=1 \]が成り立つ。
この2つの式から\[ a_n=\frac{3^n+1}{2} \]となることがわかる。(答)