センター試験 数学II・数学B 2016年度追試 第4問 解説

問題編

問題

　正八角形 $\mathrm{ P }_0\mathrm{ P }_1\mathrm{ P }_2\mathrm{ P }_3\mathrm{ P }_4\mathrm{ P }_5\mathrm{ P }_6\mathrm{ P }_7$ を考える。 $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_1 } } = \overrightarrow{ a }$, $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_7 } } = \overrightarrow{ b }$ とおく。

(1) 正八角形の1つの内角は $\myBox{アイウ}^{\circ}$ である。また、 $\angle \mathrm{ P }_1\mathrm{ P }_0\mathrm{ P }_{\myBox{エ}} = 90^{\circ}$ である。

　以下の、(2)の $\myBox{オ}$ ～ $\myBox{ケ}$ 、および(3)の $\myBox{コ}$ 、$\myBox{サ}$ については、当てはまるものを、次の 0 ～ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $\overrightarrow{ a } + \overrightarrow{ b }$
　1: $\overrightarrow{ a } + (1+\sqrt{2})\overrightarrow{ b }$
　2: $(2+\sqrt{2})\overrightarrow{ a } + (1+\sqrt{2})\overrightarrow{ b }$
　3: $\sqrt{2}\overrightarrow{ a } + \overrightarrow{ b }$
　4: $(1+\sqrt{2})\overrightarrow{ a } + \overrightarrow{ b }$
　5: $(1+\sqrt{2})\overrightarrow{ a } + (2+\sqrt{2})\overrightarrow{ b }$
　6: $\overrightarrow{ a } + \sqrt{2}\overrightarrow{ b }$
　7: $(1+\sqrt{2}) (\overrightarrow{ a } + \overrightarrow{ b })$
　8: $(2+\sqrt{2}) (\overrightarrow{ a } + \overrightarrow{ b })$
　9: $\sqrt{2} (\overrightarrow{ a } + \overrightarrow{ b })$

(2) $k=1,2,\cdots ,7$ に対して、ベクトル $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_k } }$ を $\overrightarrow{ a }$, $\overrightarrow{ b }$ を用いて表すと
\begin{eqnarray} & & \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_1 } } = \overrightarrow{ a }, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_2 } } = \myBox{オ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_3 } } = \myBox{カ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_4 } } = \myBox{キ} \\ & & \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_5 } } = \myBox{ク}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_6 } } = \myBox{ケ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_7 } } = \overrightarrow{ b } \end{eqnarray}である。

(3) $k=0,1,\cdots ,7$ に対して、対角線 $\mathrm{ \mathrm{ P }_{ k }\mathrm{ P }_{ k+3 } }$ と対角線 $\mathrm{ \mathrm{ P }_{ k+1 }\mathrm{ P }_{ k+4 } }$ の交点を $\mathrm{ Q }_k$ とする。ただし、 $\mathrm{ P }_8$, $\mathrm{ P }_9$, $\mathrm{ P }_{10}$, $\mathrm{ P }_{11}$ は、それぞれ $\mathrm{ P }_0$, $\mathrm{ P }_1$, $\mathrm{ P }_2$, $\mathrm{ P }_3$ を表すものとする。
　このとき、 $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ Q }_6 } }=\myBox{コ}$, $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ Q }_7 } }=\myBox{サ}$ である。

(4) $\overrightarrow{ \mathrm{ \mathrm{ Q }_6\mathrm{ Q }_7 } } = \left(\sqrt{\myBox{シ}}-\myBox{ス}\right)\overrightarrow{ a }$ である。したがって、正八角形 $\mathrm{ Q }_0\mathrm{ Q }_1\mathrm{ Q }_2\mathrm{ Q }_3\mathrm{ Q }_4\mathrm{ Q }_5\mathrm{ Q }_6\mathrm{ Q }_7$ の面積は、正八角形 $\mathrm{ P }_0\mathrm{ P }_1\mathrm{ P }_2\mathrm{ P }_3\mathrm{ P }_4\mathrm{ P }_5\mathrm{ P }_6\mathrm{ P }_7$ の面積の $\left( \myBox{セ}-\myBox{ソ}\sqrt{\myBox{タ}} \right)$ 倍である。

考え方

正八角形というだけでインパクトが大きいですが、各設問もなかなかハードです。計算だけで攻めていくと、行き詰まってしまいます。きれいな図形なので、できる限り図形の性質を使って解くようにしましょう。

(3)はうまく平行四辺形を見つけましょう。(4)は(3)を使えばすぐ出せますが、(3)が出なくても図形的に考えれば小さな正八角形の1辺の長さを出すことはできます。

解答編

問題

　正八角形 $\mathrm{ P }_0\mathrm{ P }_1\mathrm{ P }_2\mathrm{ P }_3\mathrm{ P }_4\mathrm{ P }_5\mathrm{ P }_6\mathrm{ P }_7$ を考える。 $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_1 } } = \overrightarrow{ a }$, $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_7 } } = \overrightarrow{ b }$ とおく。

(1) 正八角形の1つの内角は $\myBox{アイウ}^{\circ}$ である。また、 $\angle \mathrm{ P }_1\mathrm{ P }_0\mathrm{ P }_{\myBox{エ}} = 90^{\circ}$ である。

解説

正八角形に、 $\mathrm{P}_0$ からの対角線を加えると、下の図のようになります。

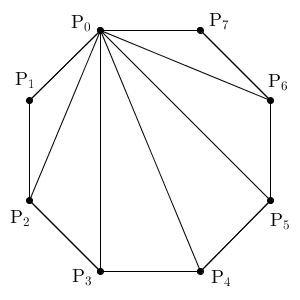
これから、正八角形の内角の和は、6つの三角形の内角の和に等しいので、 $6\times 180^{\circ}=1080^{\circ}$ となります。よって、正八角形の1つの内角は\[ 1080^{\circ} \div 8 = 135^{\circ} \]と求められます。

また、 $\angle \mathrm{P}_k \mathrm{P}_0 \mathrm{P}_{k+1}$ $(k=1,2,3,4,5,6)$ はそれぞれ同じ角度です（正八角形の外接円をかいて、弧を考えるとわかります）。なので、\[ 135^{\circ} \div 6 = 22.5^{\circ} \]となります。これを4倍すると $90^{\circ}$ になるので、\[ \angle \mathrm{ P }_1\mathrm{ P }_0\mathrm{ P }_{5} = 90^{\circ} \]となることがわかります。

解答

アイウ：135
エ：5

解答編 つづき

問題

　以下の、(2)の $\myBox{オ}$ ～ $\myBox{ケ}$ 、および(3)の $\myBox{コ}$ 、$\myBox{サ}$ については、当てはまるものを、次の 0 ～ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $\overrightarrow{ a } + \overrightarrow{ b }$
　1: $\overrightarrow{ a } + (1+\sqrt{2})\overrightarrow{ b }$
　2: $(2+\sqrt{2})\overrightarrow{ a } + (1+\sqrt{2})\overrightarrow{ b }$
　3: $\sqrt{2}\overrightarrow{ a } + \overrightarrow{ b }$
　4: $(1+\sqrt{2})\overrightarrow{ a } + \overrightarrow{ b }$
　5: $(1+\sqrt{2})\overrightarrow{ a } + (2+\sqrt{2})\overrightarrow{ b }$
　6: $\overrightarrow{ a } + \sqrt{2}\overrightarrow{ b }$
　7: $(1+\sqrt{2}) (\overrightarrow{ a } + \overrightarrow{ b })$
　8: $(2+\sqrt{2}) (\overrightarrow{ a } + \overrightarrow{ b })$
　9: $\sqrt{2} (\overrightarrow{ a } + \overrightarrow{ b })$

(2) $k=1,2,\cdots ,7$ に対して、ベクトル $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_k } }$ を $\overrightarrow{ a }$, $\overrightarrow{ b }$ を用いて表すと
\begin{eqnarray} & & \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_1 } } = \overrightarrow{ a }, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_2 } } = \myBox{オ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_3 } } = \myBox{カ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_4 } } = \myBox{キ} \\ & & \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_5 } } = \myBox{ク}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_6 } } = \myBox{ケ}, \quad \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_7 } } = \overrightarrow{ b } \end{eqnarray}である。

解説

まずは、図形的に考えてみます。その次に、計算で解く方法も書きます。最後に、補助線を使って簡単に解ける方法（ただし、補助線のひき方は難しい）も紹介します。

$\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 }$ を求めるために、 $\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 }$ について考えます。

$\overrightarrow{ a }$, $\overrightarrow{ b }$ を使って真下の方向のベクトルを作るために、次のように $\mathrm{ P }_0$ と $\mathrm{ P }_3$, $\mathrm{ P }_1$ と $\mathrm{ P }_6$ を結び、交点を A とします。

このとき、 $\angle\mathrm{ P }_1\mathrm{ P }_0\mathrm{ P }_3$ と $\angle\mathrm{ P }_0\mathrm{ P }_1\mathrm{ P }_6$ は $45^{\circ}$ となるので、 $\mathrm{ A }\mathrm{ P }_1:\mathrm{ P }_0\mathrm{ P }_1 =1:\sqrt{2}$ となります。よって、\[ \overrightarrow{ \mathrm{ P }_0 \mathrm{ A } } = \overrightarrow{ a } +\frac{1}{\sqrt{2} }\overrightarrow{ b } \]となります。これを $\sqrt{2}$ 倍したものが $\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 }$ なので、 $\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 }$ は次のようになります。
\begin{eqnarray} \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 } &=& \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_1 } +\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 } \\[5pt] &=& \overrightarrow{ a } +\sqrt{2}\overrightarrow{ \mathrm{ P }_0 \mathrm{ A } } \\[5pt] &=& \overrightarrow{ a } +(\sqrt{2}\overrightarrow{ a } +\overrightarrow{ b }) \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +\overrightarrow{ b } \\[5pt] \end{eqnarray}

次に、$\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_3 }$ を考えます。先ほどの図で、さらに $\mathrm{ P }_2$ と $\mathrm{ P }_5$ を結び、この線分と $\mathrm{ P }_0\mathrm{ P }_3$ との交点を B とします。

これから
\begin{eqnarray} \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_3 } &=& \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 } +\overrightarrow{ \mathrm{ P }_2\mathrm{ P }_3 } \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +\overrightarrow{ b } +\overrightarrow{ \mathrm{ P }_1\mathrm{ A } } +\overrightarrow{ \mathrm{ P }_0\mathrm{ A } } \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +\overrightarrow{ b } +\frac{1}{\sqrt{2} }\overrightarrow{ b } +\left(\overrightarrow{ a } +\frac{1}{\sqrt{2} }\overrightarrow{ b }\right) \\[5pt] &=& (2+\sqrt{2}) \overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } \\[5pt] \end{eqnarray}となります。

また、
\begin{eqnarray} \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_4 } &=& \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_3 } +\overrightarrow{ \mathrm{ P }_3\mathrm{ P }_4 } \\[5pt] &=& (2+\sqrt{2}) \overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } +\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_7 } \\[5pt] &=& (2+\sqrt{2}) \overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } +\overrightarrow{ b } \\[5pt] &=& (2+\sqrt{2}) (\overrightarrow{ a } +\overrightarrow{ b }) \\[5pt] \end{eqnarray}もわかり、 \begin{eqnarray} \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_5 } &=& \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_4 } +\overrightarrow{ \mathrm{ P }_4\mathrm{ P }_5 } \\[5pt] &=& (2+\sqrt{2}) (\overrightarrow{ a } +\overrightarrow{ b }) +\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_0 } \\[5pt] &=& (2+\sqrt{2}) (\overrightarrow{ a } +\overrightarrow{ b }) -\overrightarrow{ a } \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +(2+\sqrt{2})\overrightarrow{ b } \\[5pt] \end{eqnarray}もわかります。

最後に、
\begin{eqnarray} \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_6 } &=& \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_5 } +\overrightarrow{ \mathrm{ P }_5\mathrm{ P }_6 } \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +(2+\sqrt{2})\overrightarrow{ b } -\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 } \\[5pt] &=& (1+\sqrt{2}) \overrightarrow{ a } +(2+\sqrt{2})\overrightarrow{ b } -(\sqrt{2}\overrightarrow{ a } +\overrightarrow{ b }) \\[5pt] &=& \overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } \\[5pt] \end{eqnarray}となることがわかります。

なお、対称性から、 $\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_6 }$, $\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_5 }$ は、 $\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 }$, $\overrightarrow{ \mathrm{ P }_0\mathrm{ P }_3 }$ で a, b を入れ替えたものになることがわかるので、このことをチェックしてもいいでしょう。

計算だけで攻めるなら、次のようにします。はじめの1つだけ求めてみます。

$\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_2 } }$ を求めるために、 $\overrightarrow{ \mathrm{ \mathrm{ P }_1\mathrm{ P }_2 } }$ を $\overrightarrow{ a }$, $\overrightarrow{ b }$ で表すことを考えてみましょう。

正八角形の1辺の長さを l とおき、\[ \overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 } = \alpha \overrightarrow{ a } + \beta \overrightarrow{ b } \]とします。このベクトルの長さも l であり、 $\overrightarrow{ b }$ と垂直に交わることがわかるので、次の2つの式が成り立つことがわかります。
\begin{eqnarray} \left\{ \begin{array}{l} \left| \alpha \overrightarrow{ a } + \beta \overrightarrow{ b } \right| = l \\ (\alpha \overrightarrow{ a } + \beta \overrightarrow{ b }) \cdot \overrightarrow{ b } = 0 \end{array} \right. \end{eqnarray} 2つ目の式から
\begin{eqnarray} \alpha \overrightarrow{ a } \cdot \overrightarrow{ b } + \beta |\overrightarrow{ b }|^2 &=& 0 \\ \alpha l^2 \cos 135^{\circ} + \beta l^2 &=& 0 \\ \beta &=& \frac{\alpha}{\sqrt{2} } \\ \end{eqnarray}が得られます。これを1つ目の式に代入すると \begin{eqnarray} \left| \alpha \overrightarrow{ a } + \beta \overrightarrow{ b } \right|^2 &=& l^2 \\[5pt] \alpha^2 l^2 + 2\alpha\beta \overrightarrow{ a } \cdot \overrightarrow{ b } + \beta^2 l^2 &=& l^2 \\[5pt] \alpha^2 + 2\alpha\frac{\alpha}{\sqrt{2} }\times \left(-\frac{1}{\sqrt{2} }\right) + \frac{\alpha^2}{2} &=& 1 \\[5pt] \alpha^2 -\alpha^2 +\frac{\alpha^2}{2} &=& 1 \\[5pt] \alpha^2 &=& 2 \\[5pt] \end{eqnarray}図より、 $\overrightarrow{ b }$ の下向きの成分は $0$ であり、 $\overrightarrow{ a }$ と $\overrightarrow{ \mathrm{ \mathrm{ P }_1\mathrm{ P }_2 } }$ の下向きの成分の符号は同じなので、 $\alpha \gt 0$ だから、 $\alpha=\sqrt{2}$ となります。また、 \[ \beta = \frac{\alpha}{\sqrt{2} }=1 \]なので、 $\overrightarrow{ \mathrm{ P }_1\mathrm{ P }_2 } = \sqrt{2} \overrightarrow{ a } + \overrightarrow{ b }$ となるので\[ \overrightarrow{ \mathrm{ P }_0\mathrm{ P }_2 } = (1+\sqrt{2}) \overrightarrow{ a } +\overrightarrow{ b } \]となることがわかります。

計算で求めるのは、時間がかかりすぎるので、少し厳しいです。

最後に、補助線をひいて簡単に解く方法を紹介します。正八角形の外にひくので、なかなか思いつきにくいですが。

この図さえかければ
\begin{eqnarray} \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_2 } } &=& (1+\sqrt{2})\overrightarrow{ a } +\overrightarrow{ b } \\[5pt] \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_3 } } &=& (1+\sqrt{2}+1)\overrightarrow{ a } +\left( \frac{1}{\sqrt{2} }+1+\frac{1}{\sqrt{2} } \right) \overrightarrow{ b } \\[5pt] &=& (2+\sqrt{2})\overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } \\[5pt] \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_4 } } &=& \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_3 } } +\overrightarrow{ b } \\[5pt] &=& (2+\sqrt{2}) (\overrightarrow{ a } +\overrightarrow{ b }) \\[5pt] \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_5 } } &=& \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_4 } } -\overrightarrow{ a } \\[5pt] &=& (1+\sqrt{2})\overrightarrow{ a } +(2+\sqrt{2})\overrightarrow{ b } \\[5pt] \overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ P }_6 } } &=& \overrightarrow{ a } +(1+\sqrt{2})\overrightarrow{ b } \\[5pt] \end{eqnarray}となるのは、図からわかります。ただ、いきなりこの図を思いつくのは難しいかもしれません。

解答

解答編 つづき

問題

(3) $k=0,1,\cdots ,7$ に対して、対角線 $\mathrm{ \mathrm{ P }_{ k }\mathrm{ P }_{ k+3 } }$ と対角線 $\mathrm{ \mathrm{ P }_{ k+1 }\mathrm{ P }_{ k+4 } }$ の交点を $\mathrm{ Q }_k$ とする。ただし、 $\mathrm{ P }_8$, $\mathrm{ P }_9$, $\mathrm{ P }_{10}$, $\mathrm{ P }_{11}$ は、それぞれ $\mathrm{ P }_0$, $\mathrm{ P }_1$, $\mathrm{ P }_2$, $\mathrm{ P }_3$ を表すものとする。
　このとき、 $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ Q }_6 } }=\myBox{コ}$, $\overrightarrow{ \mathrm{ \mathrm{ P }_0\mathrm{ Q }_7 } }=\myBox{サ}$ である。

解説

図は次のようになっています。フリーハンドでちゃんとかくのはハードルが高いです。

四角形 $\mathrm{P}_0\mathrm{P}_1\mathrm{Q}_6\mathrm{P}_7$ は平行四辺形なので、
\begin{eqnarray} \overrightarrow{ \mathrm{P}_0\mathrm{Q}_6 } &=& \overrightarrow{ \mathrm{P}_0\mathrm{P}_1 } + \overrightarrow{ \mathrm{P}_0\mathrm{Q}_7 } \\[5pt] &=& \overrightarrow{ a } + \overrightarrow{ b } \\[5pt] \end{eqnarray}となります。

また、四角形 $\mathrm{P}_0\mathrm{P}_1\mathrm{P}_2\mathrm{Q}_7$ も平行四辺形なので、
\begin{eqnarray} \overrightarrow{ \mathrm{P}_0\mathrm{Q}_7 } &=& \overrightarrow{ \mathrm{P}_1\mathrm{P}_2 } \\[5pt] &=& \sqrt{2}\overrightarrow{ a } +\overrightarrow{ b } \\[5pt] \end{eqnarray}となります。

これを図形的に解かずに計算で解くのは、さすがに時間がかかりすぎてしまいます。

解答

コサ：03

解答編 つづき

問題

(4) $\overrightarrow{ \mathrm{ \mathrm{ Q }_6\mathrm{ Q }_7 } } = \left(\sqrt{\myBox{シ}}-\myBox{ス}\right)\overrightarrow{ a }$ である。したがって、正八角形 $\mathrm{ Q }_0\mathrm{ Q }_1\mathrm{ Q }_2\mathrm{ Q }_3\mathrm{ Q }_4\mathrm{ Q }_5\mathrm{ Q }_6\mathrm{ Q }_7$ の面積は、正八角形 $\mathrm{ P }_0\mathrm{ P }_1\mathrm{ P }_2\mathrm{ P }_3\mathrm{ P }_4\mathrm{ P }_5\mathrm{ P }_6\mathrm{ P }_7$ の面積の $\left( \myBox{セ}-\myBox{ソ}\sqrt{\myBox{タ}} \right)$ 倍である。

解説

(3)の結果から
\begin{eqnarray} \overrightarrow{ \mathrm{Q}_6\mathrm{Q}_7 } &=& \overrightarrow{ \mathrm{P}_0\mathrm{Q}_7 } -\overrightarrow{ \mathrm{P}_0\mathrm{Q}_7 } \\[5pt] &=& (\sqrt{2}\overrightarrow{ a } +\overrightarrow{ b }) -(\overrightarrow{ a } + \overrightarrow{ b }) \\[5pt] &=& (\sqrt{2}-1)\overrightarrow{ a } \\[5pt] \end{eqnarray}となります。

一辺の長さが $(\sqrt{2}-1)$ 倍になるので、面積は
\begin{eqnarray} (\sqrt{2}-1)^2 = 2-2\sqrt{2}+1=3-2\sqrt{2} \end{eqnarray}倍となります。

一辺の長さだけであれば、上の図で $\mathrm{P}_7\mathrm{Q}_7 -\mathrm{P}_7\mathrm{Q}_6$ を考えても出すことができます。

解答

シス：21
セソタ；322