センター試験 数学II・数学B 2016年度追試 第3問 解説

問題編

問題

(1) 座標平面上で、 x 座標と y 座標がともに整数である点を格子点という。
　k を自然数とする。座標平面上で、三つの不等式\[ y\geqq 0, \quad y\leqq 3x, \quad y\leqq -3x+12k \]によって表される領域を D とする。領域 D に含まれる格子点の個数を求めよう。
　領域 D は3点 $(0,0)$, $(\myBox{ア}k,\myBox{イ}k)$, $(\myBox{ウ}k,0)$ を頂点とする三角形の周および内部である。

　$k=1$ のとき、 D に含まれる格子点の個数は $\myBox{エオ}$ 個である。

　一般に、自然数 k に対し、 D に含まれる格子点の個数 p を k を用いて表そう。整数 j が $0\leqq j \leqq \mybox{ア}k$ を満たすとき、 D に含まれる格子点で x 座標が j である点は $(\myBox{カ}j+\myBox{キ})$ 個ある。したがって、 D に含まれる格子点で x 座標が $0$ 以上 $\mybox{ア}k$ 以下である点の個数 q を k を用いて表すと\[ q=\myBox{ク}k^2+\myBox{ケ}k+\myBox{コ} \]である。
　さらに、 D に含まれる格子点で x 座標が $(\mybox{ア}k+1)$ 以上 $\mybox{ウ}k$ 以下である点の個数を求めて q に加えれば p が求まり\[ p=\myBox{サシ}k^2+\myBox{ス}+\myBox{セ} \]である。

(2) n を自然数とする。四つの不等式\[ y\geqq 0, \quad y\leqq 3x, \quad y\leqq -3x+12z, \quad 1\leqq z\leqq 2n \]を満たす整数の組 $(x,y,z)$ の個数 r を求めよう。

　$n=1$ のとき、 $1\leqq z\leqq 2$ であるから、(1)により $r=\myBox{ソタ}$ である。

　一般に、自然数 n に対し、 r を n を用いて表すと\[ r=\myBox{チツ}n^3+\myBox{テト}n^2+\myBox{ナニ}n \]である。

考え方

格子点の数を数える、という問題です。順を追って求めていくうえ、 $k=1$ のときを求める設問もあり、誘導は丁寧です。計算量も、数列にしては標準的でしょう。ところどころ計算間違いをしやすいポイントはありますが、 $k=1$ のときに成り立つかを確認しながら解けば、大丈夫でしょう。

ただ、(2)は何をやっているか少しわかりづらいかもしれません。ここでやっているのは、整数の組に z が入っているので、 z の値ごとに格子点の数を足していく、ということです。

格子点は入試問題でもよく出題されますが、センターでこんなにがっつり出るのは珍しいですね。

解答編

問題

(1) 座標平面上で、 x 座標と y 座標がともに整数である点を格子点という。
　k を自然数とする。座標平面上で、三つの不等式\[ y\geqq 0, \quad y\leqq 3x, \quad y\leqq -3x+12k \]によって表される領域を D とする。領域 D に含まれる格子点の個数を求めよう。
　領域 D は3点 $(0,0)$, $(\myBox{ア}k,\myBox{イ}k)$, $(\myBox{ウ}k,0)$ を頂点とする三角形の周および内部である。

　$k=1$ のとき、 D に含まれる格子点の個数は $\myBox{エオ}$ 個である。

解説

$k=1$ のとき、図は次のようになります。

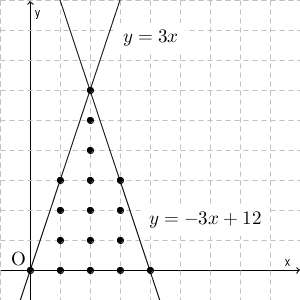
このとき、領域 D に含まれる格子点の数は\[ 1+4+7+4+1=17 \]です。

また、 k が一般の場合でも、領域 D は $k=1$ のときと同じ形の三角形になります。左下の頂点は $y=3x$ と $y=0$ の交点なので、原点となります。上側の頂点は、 $y=3x$ と $y=-3x+12k$ との交点なので、この x 座標は
\begin{eqnarray} 3x &=& -3x+12k \\ 6x &=& 12k \\ x &=& 2k \\ \end{eqnarray}となるため、この点の座標は $(2k,6k)$ となります。最後に、右下の頂点は、 $y=-3x+12k$ と $y=0$ との交点なので、座標は $(4k,0)$ となります。

実際、 $k=1$ とすると、上の図と一致していますね。

解答

アイ：26
ウ：4
エオ：17

解答編 つづき

問題

　一般に、自然数 k に対し、 D に含まれる格子点の個数 p を k を用いて表そう。整数 j が $0\leqq j \leqq \mybox{ア}k$ を満たすとき、 D に含まれる格子点で x 座標が j である点は $(\myBox{カ}j+\myBox{キ})$ 個ある。したがって、 D に含まれる格子点で x 座標が $0$ 以上 $\mybox{ア}k$ 以下である点の個数 q を k を用いて表すと\[ q=\myBox{ク}k^2+\myBox{ケ}k+\myBox{コ} \]である。

解説

$k=1$ の状況を参考にしながら考えてみましょう。

x 座標 j が $0\leqq j \leqq 2k$ のとき、というのは、三角形の左半分を指しています。このとき、 x 座標が j である点は、 $(j,0)$, $(j,1)$, $\cdots$, $(j,3j)$ なので、全部で $(3j+1)$ 個あることがわかります。

よって、 D 内の格子点で x 座標が $0$ 以上 $2k$ 以下である点の個数 q は
\begin{eqnarray} q &=& \sum_{j=0}^{2k} (3j+1) \\[5pt] &=& 3\times\frac{2k(2k+1)}{2}+(2k+1) \\[5pt] &=& 3k(2k+1)+2k+1 \\[5pt] &=& 6k^2+5k+1 \\ \end{eqnarray}となります。

ちなみに、 $k=1$ とすると、 $6+5+1=12$ となり、図から数えた $1+4+7=12$ と一致しますね。

解答

カキ：31
クケコ：651

解答編 つづき

問題

　さらに、 D に含まれる格子点で x 座標が $(\mybox{ア}k+1)$ 以上 $\mybox{ウ}k$ 以下である点の個数を求めて q に加えれば p が求まり\[ p=\myBox{サシ}k^2+\myBox{ス}+\myBox{セ} \]である。

解説

よって、 D 内の格子点の個数 p は
\begin{eqnarray} p &=& (6k^2+5k+1)+\{ (6k^2+5k+1)-(6k+1) \} \\ &=& 6k^2+5k+1 +6k^2-k \\ &=& 12k^2+4k+1 \\ \end{eqnarray}となることがわかります。

ちなみに、 $k=1$ とすると $12+4+1=17$ となり、上のエオと一致することがわかります。

解答

サシスセ：1241

解答編 つづき

問題

(2) n を自然数とする。四つの不等式\[ y\geqq 0, \quad y\leqq 3x, \quad y\leqq -3x+12z, \quad 1\leqq z\leqq 2n \]を満たす整数の組 $(x,y,z)$ の個数 r を求めよう。

　$n=1$ のとき、 $1\leqq z\leqq 2$ であるから、(1)により $r=\myBox{ソタ}$ である。

解説

$n=1$ のとき、 $1\leqq z \leqq 2$ なので、 $z=1$ と $z=2$ の場合しかありません。

$z=1$ のときは、\[ y\geqq 0, \quad y\leqq 3x, \quad y\leqq -3x+12 \]を満たす整数の組 $(x,y)$ の個数を求めればいいのですが、これは(1)で求めた格子点の数で $k=1$ としたものと一致します。よって、(1)の\[ 12k^2+4k+1 \]に代入して、 $12+4+1=17$ となります。

$z=2$ のときも同様に、(1)で求めた格子点の数の式に $k=2$ を代入して\[ 12\cdot 2^2+4\cdot 2+1=57 \]となります。

よって、このときの r は\[ r=17+57=74 \]と求められます。

解答

解答編 つづき

問題

　一般に、自然数 n に対し、 r を n を用いて表すと\[ r=\myBox{チツ}n^3+\myBox{テト}n^2+\myBox{ナニ}n \]である。

解説

結局、 r を求めるということは、(1)で求めた格子点の個数\[ 12k^2+4k+1 \]で $k=1$ としたものから $k=2n$ としたものまでを足せばいいことがわかります。よって
\begin{eqnarray} r &=& \sum_{k=1}^{2n} (12k^2+4k+1) \\[5pt] &=& 12 \times \frac{2n(2n+1)(2\cdot 2n+1)}{6} \\ & & +4\times \frac{2n(2n+1)}{2}+2n \\[5pt] &=& 4n(2n+1)(4n+1)+4n(2n+1)+2n \\[5pt] &=& 32n^3+24n^2+4n +8n^2+4n +2n \\[5pt] &=& 32n^3+32n^2+10n \\ \end{eqnarray}となります。なお、 $n=1$ とすると、ソタの答えと一致することもわかります。

解答

チツ：32
テト：32
ナニ：10