センター試験 数学II・数学B 2016年度追試 第2問 解説

問題編

問題

　三角形 ABC の周の長さは $4$ であり、 $\mathrm{ AB }=\mathrm{ AC }$ であるとする。 $\mathrm{ BC }=2a$ $(0\lt a \lt 1)$ とする。

(1) $\mathrm{ AB }=\myBox{ア}-\myBox{イ}$ である。このとき、三角形 ABC の面積は $\myBox{ウエ}\sqrt{\myBox{オ}-a}$ である。

(2) 2辺 AB, AC を $x:(1-x)$ $(0\lt x \lt 1)$ に内分する点を、それぞれ P, Q とし、直線 PQ に関して点 A と対称な点を R とする。三角形 RPQ の面積は\[ \left(\mybox{ウエ}\sqrt{\mybox{オ}-a}\right)x^{\myBox{カ}} \quad \cdots ① \]である。 $0\lt x\lt 1$ に対して、三角形 RPQ と三角形 ABC の共通部分の面積を $f(x)$ とおく。さらに $f(0)=f(1)=0$ とおく。
　$\displaystyle 0\lt x\leqq \frac{1}{2}$ のとき、点 R は三角形 ABC の内部または周上にある。したがって、 $f(x)$ は①に等しい。
　$\displaystyle \frac{1}{2} \lt x \lt 1$ のとき、直線 PR, QR と直線 BC との交点をそれぞれ $\mathrm{ P' }$, $\mathrm{ Q' }$ とする。三角形 $\mathrm{ RP'Q' }$ と三角形 ABC は相似であり、その相似比は $(\myBox{キ}x-\myBox{ク}):1$ である。したがって\[ f(x)=\left(\mybox{ウエ}\sqrt{\mybox{オ}-a}\right)\left(\myBox{ケコ}x^{\myBox{サ}}+\myBox{シ}x-1\right) \]である。
　$y=f(x)$ のグラフを調べることにより、 $f(x)$ は $\displaystyle x=\frac{\myBox{ス}}{\myBox{セ}}$ のとき、最大値 $\displaystyle \frac{\myBox{ソタ}}{\myBox{チ}} \sqrt{\mybox{オ}-a}$ をとることがわかる。

(3) 座標平面において、 $y=f(x)$ のグラフと x 軸で囲まれた図形の面積を S とおくと\[ S=\frac{\myBox{ツ}}{\myBox{テ}} \sqrt{\mybox{オ}-a} \]となる。a が $0\lt a \lt 1$ の範囲を動くとき、 S の最大値を求めよう。

　$\displaystyle S^2=\frac{\myBox{トナ}}{\myBox{ニ}}a^3+\frac{\myBox{ヌ}}{\mybox{ニ}}a^2$ である。 $S^2$ の $0\lt a \lt 1$ における増減を調べることにより、 S は $\displaystyle a=\frac{\myBox{ネ}}{\myBox{ノ}}$ のとき、最大値 $\displaystyle \frac{\myBox{ハ}\sqrt{\myBox{ヒ}} }{\myBox{フヘ}}$ をとることがわかる。

考え方

誘導は丁寧で計算量もそんなに多くないですが、図形の性質をつかったり、考えている変数が変わったりするので、落ち着いて考える必要があります。ある変数に着目しているときは、他の変数を横に置いてから計算したほうがやりやすいでしょう。

ここまで図形とからめた問題は珍しいかもしれません。

解答編

問題

　三角形 ABC の周の長さは $4$ であり、 $\mathrm{ AB }=\mathrm{ AC }$ であるとする。 $\mathrm{ BC }=2a$ $(0\lt a \lt 1)$ とする。

(1) $\mathrm{ AB }=\myBox{ア}-\myBox{イ}$ である。このとき、三角形 ABC の面積は $\myBox{ウエ}\sqrt{\myBox{オ}-a}$ である。

解説

周の長さが $4$ で、 $\mathrm{ AB }=\mathrm{ AC }$ なので、
\begin{eqnarray} \mathrm{ AB }+\mathrm{ BC }+\mathrm{ CA } &=& 4 \\ \mathrm{ AB }+2a+\mathrm{ AB } &=& 4 \\ 2\mathrm{ AB } &=& 4-2a \\ \mathrm{ AB } &=& 2-a \\ \end{eqnarray}となります。

A から BC に垂線をおろすと、三平方の定理から BC を底辺としたときの高さが
\begin{eqnarray} \sqrt{\mathrm{ AB }^2 -a^2} &=& \sqrt{(2-a)^2 -a^2} \\ &=& \sqrt{4-4a} \\ &=& 2\sqrt{1-a} \\ \end{eqnarray}と求められます。よって、三角形 ABC の面積は \begin{eqnarray} \frac{1}{2}\times 2a \times 2\sqrt{1-a} =2a\sqrt{1-a} \end{eqnarray}と求められます。

解答

アイ：2a
ウエオ：2a1

解答編 つづき

問題

(2) 2辺 AB, AC を $x:(1-x)$ $(0\lt x \lt 1)$ に内分する点を、それぞれ P, Q とし、直線 PQ に関して点 A と対称な点を R とする。三角形 RPQ の面積は\[ \left(\mybox{ウエ}\sqrt{\mybox{オ}-a}\right)x^{\myBox{カ}} \quad \cdots ① \]である。

解説

図は次のようになっています。

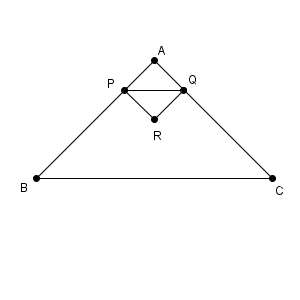
三角形 RPQ は三角形 APQ と合同で、両方とも三角形 ABC と相似です。相似比は $x:1$ なので、面積比は $x^2:1$ となります。よって、三角形 ABC の面積に $x^2$ を掛けたものが、三角形 RPQ の面積となります。先ほどの結果も使うと\[ (2a\sqrt{1-a})x^2 \]となります。

解答

カ：2

解答編 つづき

問題

$0\lt x\lt 1$ に対して、三角形 RPQ と三角形 ABC の共通部分の面積を $f(x)$ とおく。さらに $f(0)=f(1)=0$ とおく。
　$\displaystyle 0\lt x\leqq \frac{1}{2}$ のとき、点 R は三角形 ABC の内部または周上にある。したがって、 $f(x)$ は①に等しい。

解説

ここで考えているケースは、次のような図です。

このとき、三角形 RPQ と三角形 ABC の共通部分は、三角形 RPQ そのものなので、 $f(x)$ は $(2a\sqrt{1-a})x^2$ になる、ということをこの文章で説明しています。

解答編 つづき

問題

　$\displaystyle \frac{1}{2} \lt x \lt 1$ のとき、直線 PR, QR と直線 BC との交点をそれぞれ $\mathrm{ P' }$, $\mathrm{ Q' }$ とする。三角形 $\mathrm{ RP'Q' }$ と三角形 ABC は相似であり、その相似比は $(\myBox{キ}x-\myBox{ク}):1$ である。したがって\[ f(x)=\left(\mybox{ウエ}\sqrt{\mybox{オ}-a}\right)\left(\myBox{ケコ}x^{\myBox{サ}}+\myBox{シ}x-1\right) \]である。

解説

ここで考えているケースは次のような図です。

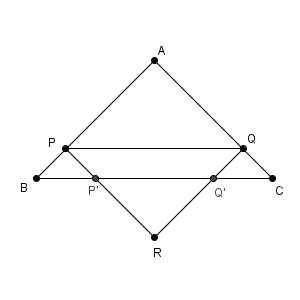
このとき、三角形 RPQ と三角形 ABC の共通部分は、台形部分になります。この面積は、直接求めるのではなく、「三角形 RPQ から不要な三角形を除く」というふうに求めます。

まずは、 AB と $\mathrm{ RP' }$ の比を求めましょう。 AB の長さを $1$ とすると、 $\mathrm{ RP }=\mathrm{ AP }=x$ です。また、 \[ \mathrm{ PP' }=\mathrm{ PB }=1-x \]となることから、
\begin{eqnarray} \mathrm{ RP' } &=& \mathrm{ RP }-\mathrm{ PP' } \\ &=& x-(1-x) \\ &=& 2x-1 \end{eqnarray}となります。よって、三角形 $\mathrm{ RP'Q' }$ と三角形 ABC との相似比は、 $(2x-1):1$ となることがわかります。

この結果から、共通部分の面積 $f(x)$ は、三角形 RPQ の面積から、三角形 ABC の面積の $(2x-1)^2$ を引けばいいので
\begin{eqnarray} f(x) &=& (2a\sqrt{1-a})x^2 -(2a\sqrt{1-a})(2x-1)^2 \\ &=& (2a\sqrt{1-a})(x^2 -4x^2+4x-1) \\ &=& (2a\sqrt{1-a})(-3x^2+4x-1) \\ \end{eqnarray}と求められます。

解答

解答編 つづき

問題

　$y=f(x)$ のグラフを調べることにより、 $f(x)$ は $\displaystyle x=\frac{\myBox{ス}}{\myBox{セ}}$ のとき、最大値 $\displaystyle \frac{\myBox{ソタ}}{\myBox{チ}} \sqrt{\mybox{オ}-a}$ をとることがわかる。

解説

先ほどの解答をまとめると、 $\displaystyle 0\lt x \leqq \frac{1}{2}$ のときは\[ f(x)=(2a\sqrt{1-a})x^2 \]であり、 $\displaystyle \frac{1}{2} \lt x \lt 1$ のときは
\begin{eqnarray} f(x) &=& (2a\sqrt{1-a})(-3x^2+4x-1) \\ &=& (2a\sqrt{1-a})\left\{ -3\left(x^2-\frac{4}{3}x\right)-1 \right\} \\[5pt] &=& (2a\sqrt{1-a})\left\{ -3\left(x-\frac{2}{3}\right)^2+\frac{1}{3} \right\} \\[5pt] \end{eqnarray}となります。

$(2a\sqrt{1-a})$ の部分は正の定数なので、この部分を除いてグラフをかくと、次のようになります。

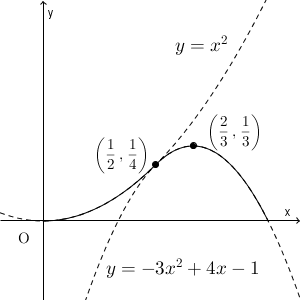
これから、 $\displaystyle x=\frac{2}{3}$ のときに最大をとることがわかります。そのときの値は $\displaystyle \frac{1}{3}$ なので、 $f(x)$ の最大値は\[ \frac{2a}{3}\sqrt{1-a} \]となります。

解答

スセ：23
ソタチ：2a3

解答編 つづき

問題

(3) 座標平面において、 $y=f(x)$ のグラフと x 軸で囲まれた図形の面積を S とおくと\[ S=\frac{\myBox{ツ}}{\myBox{テ}} \sqrt{\mybox{オ}-a} \]となる。

解説

先ほどと同じように、まずは $(2a\sqrt{1-a})$ を除いて考えます。すると、面積は
\begin{eqnarray} & & \int_0^{\frac{1}{2} } x^2 dx +\int_{\frac{1}{2} }^{1} (-3x^2+4x-1) dx \\[5pt] &=& \left[ \frac{x^3}{3} \right]_0^{\frac{1}{2} } +\left[ -x^3+2x^2-x \right]_{\frac{1}{2} }^{1} \\[5pt] &=& \frac{1}{24} +(-1+2-1)-\left(-\frac{1}{8}+\frac{2}{4}-\frac{1}{2}\right) \\[5pt] &=& \frac{1}{24}+\frac{1}{8} \\[5pt] &=& \frac{1}{6} \\[5pt] \end{eqnarray}となります。これから、 \begin{eqnarray} S &=& \frac{1}{6} \times (2a\sqrt{1-a}) \\[5pt] &=& \frac{a}{3} \sqrt{1-a} \\[5pt] \end{eqnarray}と求められます。

解答

ツテ：a3

解答編 つづき

問題

a が $0\lt a \lt 1$ の範囲を動くとき、 S の最大値を求めよう。

　$\displaystyle S^2=\frac{\myBox{トナ}}{\myBox{ニ}}a^3+\frac{\myBox{ヌ}}{\mybox{ニ}}a^2$ である。 $S^2$ の $0\lt a \lt 1$ における増減を調べることにより、 S は $\displaystyle a=\frac{\myBox{ネ}}{\myBox{ノ}}$ のとき、最大値 $\displaystyle \frac{\myBox{ハ}\sqrt{\myBox{ヒ}} }{\myBox{フヘ}}$ をとることがわかる。

解説

さきほどの結果から
\begin{eqnarray} S^2 &=& \left(\frac{a}{3} \sqrt{1-a}\right)^2 \\[5pt] &=& \frac{a^2}{9} (1-a) \\[5pt] &=& \frac{-1}{9}a^3 +\frac{1}{9}a^2 \\[5pt] \end{eqnarray}となります。

$\displaystyle g(a)=S^2=-\frac{1}{9}a^3 +\frac{1}{9}a^2$ とおいて、これを微分すると
\begin{eqnarray} g'(a) &=& -\frac{a^2}{3}+\frac{2a}{9} \\[5pt] &=& \frac{(-3a+2)a}{9} \\[5pt] \end{eqnarray}なので、$g'(a)=0$ の解は $\displaystyle a=0,\frac{2}{3}$ となります。増減表をかくと \begin{array}{c|ccccc} a & 0 & \cdots & \frac{2}{3} & \cdots & 1 \\ \hline g'(a) & 0 & + & 0 & - & \\ \hline g(a) & & \nearrow & & \searrow & \end{array}となるので、最大値をとるのは $\displaystyle a=\frac{2}{3}$ のとき。また、そのときの $g(a)=S^2$ の最大値は \begin{eqnarray} g\left(\frac{2}{3}\right) &=& -\frac{1}{9} \times \frac{8}{27} +\frac{1}{9} \times \frac{4}{9} \\[5pt] &=& \frac{2^2}{9^2} \left(-\frac{2}{3}+1\right) \\[5pt] &=& \frac{2^2}{9^2\cdot 3} \\[5pt] \end{eqnarray}となります。よって、 S の最大値は \begin{eqnarray} \frac{2}{9\sqrt{3} } = \frac{2\sqrt{3} }{27} \end{eqnarray}となることがわかります。

解答

ネノ：23
ハヒフヘ：2327