センター試験 数学II・数学B 2014年度追試 第2問 解説

【必答問題】

問題編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$座標平面上で、放物線 $y=2x^2$ を C とし、放物線 $y=-(x-p)^2+2$ を D とする。 C と D は異なる2点で交わるとし、交点の x 座標を $\alpha$, $\beta$ (ただし、 $\alpha \lt \beta$) とする。

(1) 整式 $2x^2$ と $-(x-p)^2+2$ の差を $f(x)$ とおくと\[ f(x) = 3x^2-\myBox{ア}px+p^{\bbox[1px, border:2px solid]{\ \bf{ イ }\ } }-2 \]であり、 $\alpha$ と $\beta$ は2次方程式 $f(x)=0$ の実数解である。 C と D が異なる2点で交わることから、 p のとり得る値の範囲は\[ -\sqrt{\myBox{ウ} } \lt p \lt \sqrt{\mybox{ウ} } \]である。このとき、 $\alpha +\beta$ と $\beta-\alpha$ は p を用いて
\begin{eqnarray} \alpha+\beta &=& \frac{\myBox{エ} }{\myBox{オ} }p \\[5pt] \beta-\alpha &=& \frac{\myBox{カ}\sqrt{\myBox{キ}-2p^2} }{\mybox{オ} } \quad \cdots ①\\[5pt] \end{eqnarray}と表される。

(2) $-1 \lt p \lt 1$ のとき、二つの放物線 C, D で囲まれた部分の面積を S とする。また、直線 $x=-1$ と放物線 C, D で囲まれた部分の面積を $T_1$ とし、直線 $x=1$ と放物線 C, D で囲まれた部分の面積を $T_2$ とする。 $-1\lt \alpha \lt \beta \lt 1$ であるので、 $\displaystyle T_1 = \int_{-1}^{\alpha} f(x)dx$, $\displaystyle T_2 = \int_{\beta}^1 f(x)dx$ と表される。 p が $-1\lt p \lt 1$ の範囲を動くとき、 $S+T_1+T_2$ が最小になるときの p の値を求めよう。

　定積分 $\displaystyle \int_{-1}^1 f(x)dx$ の値は p を用いて\[ \int_{-1}^1 f(x)dx = \myBox{ク}p^2-\myBox{ケ} \]と表される。さらに、定積分の性質により\[ \int_{-1}^1 f(x)dx = \myBox{コ} \]が成り立つ。 $\myBox{コ}$ に当てはまるものを、次の 0 ～ 3 のうちから一つ選べ。

　0: $T_1+T_2-S$
　1: $T_1+T_2+S$
　2: $S-T_1-T_2$
　3: $T_1+T_2+2S$

　また、①により、 S は p を用いて\[ S = \frac{\myBox{サ} }{\myBox{シス} } (\myBox{セ}-p^2)\sqrt{\myBox{ソ}-2p^2} \]と表される。

　そこで、 $q=\sqrt{\mybox{ソ}-2p^2}$ とおいて、 $S+T_1+T_2$ を q を用いて表すと\[ S+T_1+T_2 = \frac{\myBox{タ} }{\myBox{チツ} }-q^2+\myBox{テ} \]となる。

　$-1\lt p \lt 1$ のとき、 q のとり得る値の範囲は $\myBox{ト} \lt q \leqq \sqrt{\myBox{ナ} }$ である。 q がこの範囲を動くときの $S+T_1+T_2$ の値の増減を調べることにより、 $S+T_1+T_2$ は $\displaystyle q=\frac{\myBox{ニ} }{\myBox{ヌ} }$ のとき、すなわち、 $\displaystyle p=\pm\frac{\sqrt{\myBox{ネノ} }}{\myBox{ハ} }$ のとき、最小になることがわかる。

考え方

(1)の後半で、解の差を求める部分は、直接計算したほうが早いでしょう。差を2乗した値を求める方針でも解くことはできますが、計算量はあまり変わらないです。

(2)は、まず積分と面積の関係をきちんと把握しましょう。サ～ソの部分は、直線と放物線に囲まれた部分の面積を求める公式を使います（新課程では詳しく習わない可能性があります）。この公式を知らないと、ここ以降の計算は絶望的です。

計算が複雑すぎたり多すぎるわけではありませんが、日ごろからよく練習しておかないと最後まで到達するのは難しいです。

---

【必答問題】

解答編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$座標平面上で、放物線 $y=2x^2$ を C とし、放物線 $y=-(x-p)^2+2$ を D とする。 C と D は異なる2点で交わるとし、交点の x 座標を $\alpha$, $\beta$ (ただし、 $\alpha \lt \beta$) とする。

(1) 整式 $2x^2$ と $-(x-p)^2+2$ の差を $f(x)$ とおくと\[ f(x) = 3x^2-\myBox{ア}px+p^{\bbox[1px, border:2px solid]{\ \bf{ イ }\ } }-2 \]であり、 $\alpha$ と $\beta$ は2次方程式 $f(x)=0$ の実数解である。 C と D が異なる2点で交わることから、 p のとり得る値の範囲は\[ -\sqrt{\myBox{ウ} } \lt p \lt \sqrt{\mybox{ウ} } \]である。

解説

2つの式を引いたものが $f(x)$ なので
\begin{eqnarray} f(x) &=& 2x^2 -\{ -(x-p)^2+2 \} \\ &=& 2x^2 -\{ -x^2+2px-p^2+2 \} \\ &=& 3x^2 -2px +p^2 -2 \\ \end{eqnarray}となります。

C と D が異なる2点で交わることは、 $f(x)=0$ が異なる2つの実数解を持つことと同値なので、この判別式が0より大きくなることと同値です。よって
\begin{eqnarray} (-2p)^2 -4\cdot 3\cdot(p^2-2) &\gt & 0 \\ p^2 -3p^2+6 &\gt & 0 \\ p^2-3 &\lt & 0 \\ \end{eqnarray}から、 p のとり得る値の範囲は $-\sqrt{3} \lt p \lt \sqrt{3}$ となることがわかります。

解答

アイウ：223

解答編 つづき

問題

このとき、 $\alpha +\beta$ と $\beta-\alpha$ は p を用いて
\begin{eqnarray} \alpha+\beta &=& \frac{\myBox{エ} }{\myBox{オ} }p \\[5pt] \beta-\alpha &=& \frac{\myBox{カ}\sqrt{\myBox{キ}-2p^2} }{\mybox{オ} } \quad \cdots ①\\[5pt] \end{eqnarray}と表される。

解説

$f(x)=3x^2 -2px +p^2 -2$ なので、 $\alpha +\beta$ は解と係数の関係から $\displaystyle -\frac{-2p}{3}=\frac{2}{3}p$ となります。

また、一般的に、 $ax^2+bx+c=0$ が異なる2つの実数解を持つとき、この判別式を D とすると、この解の差は
\begin{eqnarray} \frac{-b+\sqrt{D} }{2a} -\frac{-b-\sqrt{D} }{2a} = \frac{\sqrt{D} }{a} \end{eqnarray}となるので、 $\beta-\alpha$ は次のように求められます。 \begin{eqnarray} \frac{\sqrt{(-2p)^2-4\cdot 3 \cdot(p^2-2)} }{3} &=& \frac{2\sqrt{p^2-3p^2+6} }{3} \\[5pt] &=& \frac{2\sqrt{6-2p^2} }{3} \\[5pt] \end{eqnarray}

解答

エオ：23
カキ：26

解答編 つづき

問題

(2) $-1 \lt p \lt 1$ のとき、二つの放物線 C, D で囲まれた部分の面積を S とする。また、直線 $x=-1$ と放物線 C, D で囲まれた部分の面積を $T_1$ とし、直線 $x=1$ と放物線 C, D で囲まれた部分の面積を $T_2$ とする。 $-1\lt \alpha \lt \beta \lt 1$ であるので、 $\displaystyle T_1 = \int_{-1}^{\alpha} f(x)dx$, $\displaystyle T_2 = \int_{\beta}^1 f(x)dx$ と表される。 p が $-1\lt p \lt 1$ の範囲を動くとき、 $S+T_1+T_2$ が最小になるときの p の値を求めよう。

解説

図は次のようになっています。

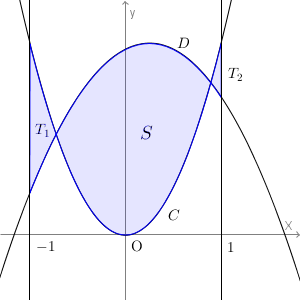
ちなみに、「 $-1\lt \alpha \lt \beta \lt 1$ であるので」と書かれています。このことはそのまま使ってもいいのですが、なぜこうなるかは次のように計算するとわかります（解答には関係ないので、ここは飛ばしてもかまいません）。まず、 $\beta \lt 1$ については
\begin{eqnarray} & & \beta \lt 1 \\[5pt] &\iff& \frac{p+\sqrt{6-2p^2} }{3} \lt 1 \\[5pt] &\iff& \sqrt{6-2p^2} \lt 3-p \\[5pt] \end{eqnarray}であり、 $-\sqrt{3} \lt p \lt \sqrt{3}$ だから両辺が正なので \begin{eqnarray} & & \sqrt{6-2p^2} \lt 3-p \\ &\iff& 6-2p^2 \lt (3-p)^2 \\ &\iff& 0 \lt 3p^2-6p+3 \\ &\iff& 0 \lt (p-1)^2 \\ \end{eqnarray}となります。最後の式から、 $p\ne 1$ のときに $\beta \lt 1$ が成り立つことがわかります。(2)で考える範囲は $-1 \lt p \lt 1$ なので、 $\beta \lt 1$ となるわけですね。

$-1\lt \alpha$ も同様に考えると
\begin{eqnarray} & & \alpha \gt -1 \\[5pt] &\iff& \frac{p-\sqrt{6-2p^2} }{3} \gt -1 \\[5pt] &\iff& \sqrt{6-2p^2} \lt p+3 \\[5pt] &\iff& 6-2p^2 \lt p^2+6p+9 \\ &\iff& 0 \lt 3p^2+6p+3 \\ &\iff& 0 \lt (p+1)^2 \\ \end{eqnarray}となるから、 $p\ne -1$ のときに $-1 \lt \alpha$ が成り立つことがわかります。(2)で考える範囲は $-1 \lt p \lt 1$ なので、 $-1 \lt \alpha$ となることがわかります。

以上から、 $-1 \lt p \lt 1$ の範囲では、 $-1\lt \alpha \lt \beta \lt 1$ が成り立つことがわかります。

解答編 つづき

問題

　定積分 $\displaystyle \int_{-1}^1 f(x)dx$ の値は p を用いて\[ \int_{-1}^1 f(x)dx = \myBox{ク}p^2-\myBox{ケ} \]と表される。さらに、定積分の性質により\[ \int_{-1}^1 f(x)dx = \myBox{コ} \]が成り立つ。 $\myBox{コ}$ に当てはまるものを、次の 0 ～ 3 のうちから一つ選べ。

　0: $T_1+T_2-S$
　1: $T_1+T_2+S$
　2: $S-T_1-T_2$
　3: $T_1+T_2+2S$

解説

定積分 $\displaystyle \int_{-1}^1 f(x)dx$ を計算すると
\begin{eqnarray} & & \int_{-1}^1 (3x^2 -2px +p^2 -2) dx \\[5pt] &=& \left[ x^3 -px^2 +p^2x -2x \right]_{-1}^1 \\[5pt] &=& ( 1^3 -p\cdot 1^2 +p^2 \cdot 1 -2\cdot 1 ) \\ & & -\left\{ (-1)^3 -p\cdot (-1)^2 +p^2 \cdot (-1) -2\cdot (-1) \right\} \\[5pt] &=& (1 -p +p^2 -2) \\ & & -( -1 -p -p^2 +2) \\[5pt] &=& (p^2-p-1) -( -p^2-p+1) \\[5pt] &=& 2p^2-2 \\[5pt] \end{eqnarray}となります。

また、グラフを見ると、 $\alpha \lt x \lt \beta$ の範囲では D の方が上で、他の範囲では C の方が上となっています。 $f(x)$ は C が表す式から D が表す式を引いたものなので、\[ \int_{-1}^1 f(x) dx = T_1+T_2-S \]となります。

解答

クケ：22
コ：0

解答編 つづき

問題

　また、①により、 S は p を用いて\[ S = \frac{\myBox{サ} }{\myBox{シス} } (\myBox{セ}-p^2)\sqrt{\myBox{ソ}-2p^2} \]と表される。

解説

一般に\[ \int_a^b (x-a)(x-b) dx = -\frac{1}{6}(b-a)^3 \]が成り立ちます。これを使うと
\begin{eqnarray} S &=& -\int_{\alpha}^{\beta} (3x^2 -2px +p^2 -2) dx \\[5pt] &=& -3\int_{\alpha}^{\beta} (x-\alpha)(x-\beta) dx \\[5pt] &=& -3 \times \left(-\frac{1}{6}\right) (\beta-\alpha)^3 \\[5pt] &=& \frac{1}{2} \left(\frac{2\sqrt{6-2p^2} }{3}\right)^3 \\[5pt] &=& \frac{1}{2} \times \frac{8(6-2p^2)\sqrt{6-2p^2} }{27} \\[5pt] &=& \frac{4(6-2p^2)\sqrt{6-2p^2} }{27} \\[5pt] &=& \frac{8}{27} (3-p^2) \sqrt{6-2p^2} \\[5pt] \end{eqnarray}となります。

解答

タチツテ：82736

解答編 つづき

問題

　そこで、 $q=\sqrt{\mybox{ソ}-2p^2}$ とおいて、 $S+T_1+T_2$ を q を用いて表すと\[ S+T_1+T_2 = \frac{\myBox{タ} }{\myBox{チツ} }-q^2+\myBox{テ} \]となる。

解説

定積分を計算した、ク・ケ・コの部分から
\begin{eqnarray} S+T_1+T_2 &=& T_1+T_2-S+2S \\ &=& \int_{-1}^1 f(x)dx+2S \\ &=& 2p^2-2+2S \\ \end{eqnarray}と変形できます。

また、サ～ソの結果からさらに変形すると
\begin{eqnarray} S+T_1+T_2 &=& 2p^2-2+2 \times \frac{8}{27} (3-p^2) \sqrt{6-2p^2} \end{eqnarray}となります。

ここで、 $q=\sqrt{6-2p^2}$ として、上の p の部分をすべて変換します。

$q^2=6-2p^2$ なので、カッコで囲まれた $3-p^2$ は $\displaystyle \frac{q^2}{2}$ となります。また、 $2p^2 = 6-q^2$ と変形できるので、これらを上の式に代入すると
\begin{eqnarray} S+T_1+T_2 &=& (6-q^2)-2 +2 \times \frac{8}{27} \times \frac{q^2}{2} \times q \\[5pt] &=& 6-q^2-2 + \frac{8}{27} q^3 \\[5pt] &=& \frac{8}{27}q^3 -q^2 +4 \\[5pt] \end{eqnarray}となります。

解答

タチツテ：8274

解答編 つづき

問題

　$-1\lt p \lt 1$ のとき、 q のとり得る値の範囲は $\myBox{ト} \lt q \leqq \sqrt{\myBox{ナ} }$ である。 q がこの範囲を動くときの $S+T_1+T_2$ の値の増減を調べることにより、 $S+T_1+T_2$ は $\displaystyle q=\frac{\myBox{ニ} }{\myBox{ヌ} }$ のとき、すなわち、 $\displaystyle p=\pm\frac{\sqrt{\myBox{ネノ} }}{\myBox{ハ} }$ のとき、最小になることがわかる。

解説

$q=\sqrt{6-2p^2}$ とおいていました。また、 $-1\lt p \lt 1$ のとき、$0 \leqq 2p^2 \lt 2$ なので、 $6\geqq 6-2p^2 \gt 6-2=4$ となります。よって、 q の範囲は、 $2\lt q \leqq \sqrt{6}$ となります。

タ～テで求めた通り\[ S+T_1+T_2=\frac{8}{27}q^3 -q^2 +4 \]となります。この右辺を $g(q)$ とおくと
\begin{eqnarray} g'(q) &=& \frac{8}{27}\times 3q^2 -2q \\[5pt] &=& \frac{8}{9}q^2 -2q \\[5pt] &=& \frac{8}{9}q \left(q-\frac{9}{4}\right) \\[5pt] \end{eqnarray}となるので、 $g'(q)=0$ となるとき $\displaystyle q=0,\frac{9}{4}$ となります。

ここで、 $\displaystyle \frac{9}{4}=\sqrt{\frac{81}{16} }$ であり、 $\displaystyle \sqrt{6} = \sqrt{\frac{96}{16} }$ なので、 $\displaystyle \frac{9}{4}\lt \sqrt{6}$ がわかります。このことも踏まえると、増減表は次のようになります。
\begin{array}{c|ccccc} q & 2 & \cdots & \frac{9}{4} & \cdots & \sqrt{6} \\ \hline g' & & - & 0 & + & \\ \hline g & & \searrow & & \nearrow & \end{array}これより、 $g(q)$ 、つまり、 $S+T_1+T_2$ が最小となるのは $\displaystyle q=\frac{9}{4}$ のときであることがわかります。また、 $q=\sqrt{6-2p^2}$ なので \begin{eqnarray} \frac{9}{4} &=& \sqrt{6-2p^2} \\[5pt] \frac{81}{16} &=& 6-2p^2 \\[5pt] 2p^2 &=& 6-\frac{81}{16} \\[5pt] &=& \frac{15}{16} \\[5pt] p^2 &=& \frac{15}{32} \\[5pt] p &=& \pm \sqrt{ \frac{15}{32} } \\[5pt] &=& \pm \frac{\sqrt{30} }{8} \\[5pt] \end{eqnarray}のとき、であることがわかります。

解答

トナ：26
ニヌ：94
ネノハ：308