センター試験 数学II・数学B 2014年度追試 第1問 [2] 解説

【必答問題】

問題編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$$\displaystyle 0\leqq \theta \leqq \frac{\pi}{2}$ として、\[ f(\theta) = 8 \sin\theta \cos\theta +6\cos^2\theta \]とおく。

(1) 2倍角の公式と三角関数の合成を用いると
\begin{eqnarray} f(\theta) &=& \myBox{ソ}\sin2\theta +\myBox{タ}(\cos2\theta+1) \\ &=& \myBox{チ}\sin(2\theta+\alpha) +\mybox{タ} \quad \cdots ⑤ \\ \end{eqnarray}となる。ただし、 $\alpha$ は\[ \sin\alpha = \frac{\myBox{ツ} }{\mybox{チ} }, \ \cos\alpha = \frac{\myBox{テ} }{\mybox{チ} }, \ 0 \lt \alpha \lt \frac{\pi}{2} \]を満たすものとする。

　$\displaystyle 0\leqq \theta\leqq \frac{\pi}{2}$ のとき、 $2\theta+\alpha$ のとり得る値の範囲は\[ \alpha \leqq 2\theta+\alpha \leqq \pi+\alpha \]であるから、 $\displaystyle 0 \lt \alpha \lt \frac{\pi}{2}$ に注意すると、 $\sin(2\theta+\alpha)$ は、 $\theta=\myBox{ト}$ で最大値 $1$ 、 $\theta=\myBox{ナ}$ で最小値 $\displaystyle -\frac{\myBox{ニ} }{\myBox{ヌ} }$ をとることがわかる。ただし、 $\myBox{ト}$, $\myBox{ナ}$ については、当てはまるものを、次の 0 ～ 5 のうちから一つずつ選べ。

　0: $0$

　1: $\displaystyle \frac{\pi}{4} -\alpha$

　2: $\displaystyle \frac{\pi}{4} -\frac{\alpha}{2}$

　3: $\displaystyle \frac{\pi}{2} -\alpha$

　4: $\displaystyle \frac{\pi}{2} -\frac{\alpha}{2}$

　5: $\displaystyle \frac{\pi}{2}$

　以上のことから、 $\displaystyle 0\leqq \theta\leqq \frac{\pi}{2}$ のとき、 $f(\theta)$ のとり得る値の範囲は $\myBox{ネ} \leqq f(\theta) \leqq \myBox{ノ}$ である。

(2) $f(\theta)=6$, $\displaystyle 0 \leqq \theta \leqq \frac{\pi}{2}$ を満たす $\theta$ を求めよう。⑤を用いると、 $f(\theta)=6$ から\[ \sin(2\theta+\alpha) = \frac{\myBox{ハ} }{\myBox{ヒ} } \]である。ここで、 $\displaystyle \sin\alpha = \frac{\mybox{ツ} }{\mybox{チ} }$ と、すべての x について $\sin(\pi-x) = \myBox{フ}$ であることに注意すると、求める $\theta$ は $\myBox{ヘ}$ と $\myBox{ホ}$ であることがわかる。ただし、 $\myBox{フ}$ については、当てはまるものを、次の 0 ～ 3 のうちから一つ選べ。

　0: $\cos x$
　1: $-\cos x$
　2: $\sin x$
　3: $-\sin x$

また、 $\myBox{ヘ}$, $\myBox{ホ}$ については、当てはまるものを、次の 0 ～ 5 のうちから一つずつ選べ。 $\mybox{ヘ}$ と $\mybox{ホ}$ は解答の順序を問わない。

　0: $0$
　1: $\alpha$
　2: $\displaystyle \frac{\pi}{2}-\alpha$

　3: $\displaystyle \frac{\pi}{2}$
　4: $\pi-2\alpha$
　5: $\pi-\alpha$

考え方

前半は、倍角の公式、合成を使って、式の最大・最小を求める問題です。角度のとり得る範囲には注意が必要ですが、問題としてはよくある流れです。最大・最小は、図をかいて考えましょう。

後半は式の値から角度を求める問題です。2つある答えのうち片方はすぐにわかるため、難易度は高くありません。もう一つの解も、単位円を書いて考えれば、すぐに条件式を得られるでしょう。

---

【必答問題】

解答編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$$\displaystyle 0\leqq \theta \leqq \frac{\pi}{2}$ として、\[ f(\theta) = 8 \sin\theta \cos\theta +6\cos^2\theta \]とおく。

(1) 2倍角の公式と三角関数の合成を用いると
\begin{eqnarray} f(\theta) &=& \myBox{ソ}\sin2\theta +\myBox{タ}(\cos2\theta+1) \\ &=& \myBox{チ}\sin(2\theta+\alpha) +\mybox{タ} \quad \cdots ⑤ \\ \end{eqnarray}となる。ただし、 $\alpha$ は\[ \sin\alpha = \frac{\myBox{ツ} }{\mybox{チ} }, \ \cos\alpha = \frac{\myBox{テ} }{\mybox{チ} }, \ 0 \lt \alpha \lt \frac{\pi}{2} \]を満たすものとする。

解説

2倍角の公式 $\sin 2\theta = 2\sin\theta \cos\theta$ と $\cos 2\theta = 2\cos^2\theta -1$ を使うと
\begin{eqnarray} f(\theta) &=& 8\sin\theta \cos\theta +6 \cos^2 \theta \\ &=& 4\times 2\sin\theta \cos\theta +3\times 2\cos^2 \theta \\ &=& 4\sin 2\theta +3(\cos 2\theta +1) \\ \end{eqnarray}となります。

次に、 $4\sin 2\theta$ と $3\cos 2\theta$ の和を、三角関数の合成を使ってまとめると、\[ \sin\alpha = \frac{3}{\sqrt{4^2+3^2} }=\frac{3}{5} \]かつ $\displaystyle \cos\alpha=\frac{4}{5}$ となる $\alpha$ を使って、\[ 4\sin 2\theta +3\cos 2\theta = 5\sin(2\theta+\alpha) \]と書けます。また、 $\sin\alpha$ も $\cos\alpha$ も正なので、 $\displaystyle 0 \lt \alpha \lt \frac{\pi}{2}$ となるように $\alpha$ をとることができます。

この合成を使うと
\begin{eqnarray} f(\theta) &=& 5\sin (2\theta+\alpha) +3 \\ \end{eqnarray}となります。

解答

ソタチ：435
ツテ：34

解答編 つづき

問題

　$\displaystyle 0\leqq \theta\leqq \frac{\pi}{2}$ のとき、 $2\theta+\alpha$ のとり得る値の範囲は\[ \alpha \leqq 2\theta+\alpha \leqq \pi+\alpha \]であるから、 $\displaystyle 0 \lt \alpha \lt \frac{\pi}{2}$ に注意すると、 $\sin(2\theta+\alpha)$ は、 $\theta=\myBox{ト}$ で最大値 $1$ 、 $\theta=\myBox{ナ}$ で最小値 $\displaystyle -\frac{\myBox{ニ} }{\myBox{ヌ} }$ をとることがわかる。ただし、 $\myBox{ト}$, $\myBox{ナ}$ については、当てはまるものを、次の 0 ～ 5 のうちから一つずつ選べ。

　0: $0$

　1: $\displaystyle \frac{\pi}{4} -\alpha$

　2: $\displaystyle \frac{\pi}{4} -\frac{\alpha}{2}$

　3: $\displaystyle \frac{\pi}{2} -\alpha$

　4: $\displaystyle \frac{\pi}{2} -\frac{\alpha}{2}$

　5: $\displaystyle \frac{\pi}{2}$

　以上のことから、 $\displaystyle 0\leqq \theta\leqq \frac{\pi}{2}$ のとき、 $f(\theta)$ のとり得る値の範囲は $\myBox{ネ} \leqq f(\theta) \leqq \myBox{ノ}$ である。

解説

$2\theta+\alpha$ のとり得る範囲は\[ \alpha \leqq 2\theta+\alpha \leqq \pi+\alpha \]なので、単位円を使って表すと、次の赤い部分になります。

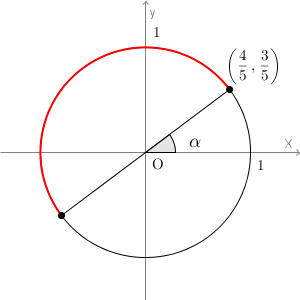
$\alpha$ の値はわかりませんが、第1象限から第3象限までという、大体の範囲が分かれば大丈夫です。 $\sin(2\theta+\alpha)$ の最大値・最小値は、上の赤い部分の y 座標の最大値・最小値を見ればわかります。

よって、最大値は $1$ で、そのときの $\theta$ は $\displaystyle 2\theta+\alpha=\frac{\pi}{2}$ のとき、つまり\[ \theta = \frac{\pi}{4}-\frac{\alpha}{2} \]のときであることがわかります。

また、最小値は、 $\displaystyle \theta=\frac{\pi}{2}$ のときにとり、値は\[ \sin(\pi+\alpha)= -\sin\alpha = -\frac{3}{5} \]であることがわかります。

$\sin(2\theta+\alpha)$ を5倍して3を足したものが $f(\theta)$ なので
\begin{eqnarray} -\frac{3}{5} & \leqq & \sin(\pi+\alpha) & \leqq & 1 \\[5pt] -\frac{3}{5}\times 5+3 & \leqq & 5\sin(\pi+\alpha)+3 & \leqq & 1\times5+3 \\[5pt] 0 & \leqq & f(\theta) & \leqq & 8 \\[5pt] \end{eqnarray}となることがわかります。

解答

トナニヌ：2535
ネノ：08

解答編 つづき

問題

(2) $f(\theta)=6$, $\displaystyle 0 \leqq \theta \leqq \frac{\pi}{2}$ を満たす $\theta$ を求めよう。⑤を用いると、 $f(\theta)=6$ から\[ \sin(2\theta+\alpha) = \frac{\myBox{ハ} }{\myBox{ヒ} } \]である。

解説

⑤を変形して
\begin{eqnarray} 5\sin (2\theta+\alpha) +3 &=& 6 \\[5pt] \sin (2\theta+\alpha) &=& \frac{3}{5} \\[5pt] \end{eqnarray}が得られます。

解答

ハヒ：35

解答編 つづき

問題

ここで、 $\displaystyle \sin\alpha = \frac{\mybox{ツ} }{\mybox{チ} }$ と、すべての x について $\sin(\pi-x) = \myBox{フ}$ であることに注意すると、求める $\theta$ は $\myBox{ヘ}$ と $\myBox{ホ}$ であることがわかる。ただし、 $\myBox{フ}$ については、当てはまるものを、次の 0 ～ 3 のうちから一つ選べ。

　0: $\cos x$
　1: $-\cos x$
　2: $\sin x$
　3: $-\sin x$

また、 $\myBox{ヘ}$, $\myBox{ホ}$ については、当てはまるものを、次の 0 ～ 5 のうちから一つずつ選べ。 $\mybox{ヘ}$ と $\mybox{ホ}$ は解答の順序を問わない。

　0: $0$
　1: $\alpha$
　2: $\displaystyle \frac{\pi}{2}-\alpha$

　3: $\displaystyle \frac{\pi}{2}$
　4: $\pi-2\alpha$
　5: $\pi-\alpha$

解説

先ほど得た $\displaystyle \sin (2\theta+\alpha) = \frac{3}{5}$ を解くのですが、そもそも $\displaystyle \sin \alpha = \frac{3}{5}$ なので、 $\theta=0$ が解になることがすぐにわかります。

さきほどの図からもわかりますが、 $\theta=0$ のとき（赤い線のスタート）と同じ y 座標になるのは、もう一つあります。図からもわかりますが、 $\sin(\pi-\alpha)$ のときですね。一般的に、 $\sin(\pi-x) = \sin x$ が成り立つので、\[ \sin(\pi-\alpha)=\sin\alpha=\frac{3}{5} \]となるからです。よって、このときも解となります。このときの $\theta$ は
\begin{eqnarray} 2\theta+\alpha &=& \pi-\alpha \\[5pt] 2\theta &=& \pi-2\alpha \\[5pt] \theta &=& \frac{\pi}{2}-\alpha \\[5pt] \end{eqnarray}と求められます。

以上から、 $\displaystyle \theta = 0, \frac{\pi}{2}-\alpha$ のときに $f(\theta)=6$ となることがわかります。

解答

フ：2
ヘホ：0,2