AtCoder ABC 230 E - Fraction Floor Sum (500点) 解説

問題

問題文は本家サイトにあります：AtCoder ABC 230 E - Fraction Floor Sum

問題概要

正の整数 $N$ に対して、 $\displaystyle \sum_{i=1}^N \left[ \frac{N}{i} \right]$ を求めなさい。

制約

入力は整数
$1\leqq N \leqq 10^{12}$

解説

最大で $10^{12}$ の整数が入力されるので、そのまま計算すると間に合いません。そこで、早く計算する方法を考えます。

$N=10$ のときを考えてみます。 $i=1$ から $i=10$ までにたいして、 $\left[\dfrac{10}{i}\right]$ を計算してみます。この個数は、並べて書くと、点の個数に対応します。

これは、反比例のグラフ $y=\dfrac{10}{x}$ を使うと、このグラフ上かグラフより下の部分で、 $x$ 軸より上、 $y$ 軸より右の部分にある格子点（両方の座標が整数の点）の個数となります。

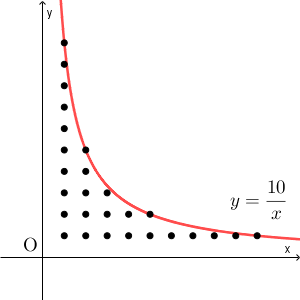
これを各 $x$ について単純に足し合わせていくと間に合わないのですが、上のグラフを見れば、対称性があることに気づきます。直線 $y=x$ をひいてみると、次のようになります。

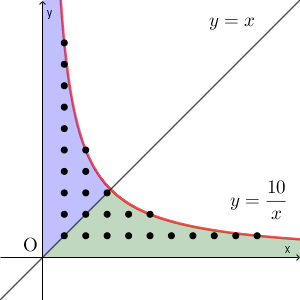
図の青い部分と緑の部分は、 $y=x$ について対称になります。 $i\cdot j\leqq N$ なら $j\cdot i\leqq N$ が成り立つことからもわかります。こうして、青い部分を計算すれば、緑の部分も求められることがわかります。また、青い部分の右端にある格子点は、 $y=x$ と $y=N/x$ の交点のところなので、 $x$ 座標は $[\sqrt{N}]$ です。 $1$ から $[\sqrt{N}]$ に対して計算する程度であれば間に合います。

以上のことから、次のように計算すれば間に合います。 $i=1$ から $i=[\sqrt{N}]$ に対して、 $\left[ \dfrac{N}{i} \right] -i$ を計算し、足し合わせていきます。これにより、青い部分内にある格子点のうち、 $y=x$ より上にある格子点の個数が計算できます。これを2倍し、あとで、$y=x$ 上にある点を足していけば答えになります。

提出 #27683072

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int main() {
  ll N; cin >> N;
  ll sq = sqrt(N);
  ll ans = 0;
  for (ll i = 1; i <= sq; i++) {
    ans += N / i - i;
  }
  ans *= 2;
  for (ll i = 1; i <= sq; i++) {
    ans++;
  }
  cout << ans << '\n';
  return 0;
}