【標準】文字の入った二次不等式

ここでは、定数の入った二次不等式を考えてみます。基本的には普通の二次不等式と同じようにグラフをかいて考えるのですが、気をつけないといけない点があります。

例題

左辺は $(x-m)(x-2)$ と因数分解できます。二次不等式はグラフをかいて考えればいいので、この因数分解した式をもとにグラフをかいてみます。

といきたいところなんですが、ここで問題が発生します。グラフは x 軸と共有点を持つことがわかるのですが、どっちが m でどっちが $2$ かがわからないんですよね。どっちがどっちかは決まっていないので、場合分けをして考えなければいけません。

例えば、まずはこういうグラフになる場合がありますよね。

しかし、こういう場合だけとは限りません。 m と $2$ の大小関係が入れ替わる場合もありますよね。

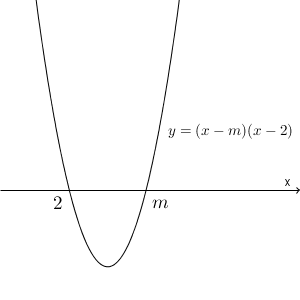
ちなみに、1つ目は $m\lt 2$ のとき、2つ目は $m\gt 2$ のときですね。ただ、これだけでは足りません。そもそも2点で交わっていない、次のケースがあるんですね。

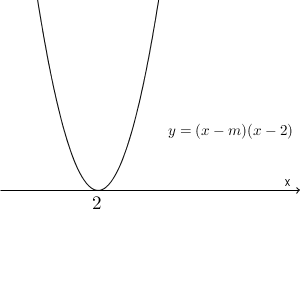
$m=2$ のときです。この3つの場合があり、それぞれ解が異なります。

まず、1つ目の場合、 x 軸より下の部分を考えると、 $m\lt x\lt 2$ となります。2つ目の場合は、 $2\lt x\lt m$ となります。3つ目の場合は、 x 軸より下の部分がないので、「解なし」が答えになります。

まとめると、解は次のようになります。

　$m\lt 2$ のときは、 $m\lt x\lt 2$
　$m= 2$ のときは、解なし
　$m\gt 2$ のときは、 $2\lt x\lt m$

この3つまとめたものが答えです。長いですが、状況によって解が変わるので、それぞれ分けて全部まとめて答えないといけません。

おわりに

文字が入っている場合は、状況が変わることに自分で気づいて場合分けをしないといけないケースがあります。状況を決め打ちしていないかどうか、よく考えて解くようにしましょう。