【標準】放物線の対称移動

🕒 2016/07/20 🔄 2023/05/01

【標準】放物線の平行移動（変数の置き換え）などの記事で、平行移動した放物線の方程式を考えました。この記事では、これに関連して、対称移動した放物線の方程式を考えていきます。

📘 目次

点の対称移動

放物線の対称移動を考える前に、点の対称移動を考えましょう。

直線や点に関して、それと対称な位置に図形を移動させることを対称移動といいます。グラフを扱うときによく出てくるのは、x 軸に関する対称移動、y 軸に関する対称移動、原点に関する対称移動の3種類です。移動によって、各点がどう移動するか見てみましょう。

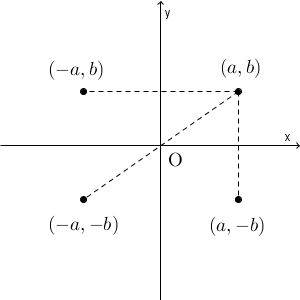
x 軸に関して対称移動する、ということは、x 軸で平面を折りたたんだときに一致するように、上下に移動するということですね。y 軸に関しての対称移動は、左右への移動です。原点に関する対称移動は、その両方を合わせたものですね。

移動後の点の座標をまとめると、次のようになります。

点の対称移動

点 $(a,b)$ は、対称移動によってそれぞれ次の点に移動する。

x 軸に関する対称移動： $(a,-b)$
y 軸に関する対称移動： $(-a,b)$
原点に関する対称移動： $(-a,-b)$

これを踏まえて、放物線の対称移動を考えていきましょう。

対称移動した後の放物線の方程式

平行移動した後の放物線の方程式を求める方法は、頂点に着目する方法と変数を置き換える方法とがありました。対称移動の場合も、同様に2通りで考えることができます。

例えば、放物線 $y=x^2-2x+3$ を x 軸に関して対称移動した場合を考えてみましょう。

まずは、頂点に着目して、移動後の放物線の方程式を求めてみます。頂点の座標を求めるために、次のような式変形をします。
\begin{eqnarray} y &=& x^2-2x+3 \\ &=& (x-1)^2+2 \\ \end{eqnarray}このことから、頂点は $(1,2)$ となります。なので、対称移動後の頂点は $(1,-2)$ となります。ここですぐに移動後の放物線の方程式に行きたいところなんですが、ちょっとしたひっかけがあります。グラフをかいてみましょう。

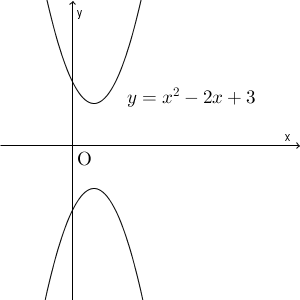
x 軸に関して対称移動した場合、放物線の上下も変わってしまいます。平行移動するときはこんなことは起こらないのですが、対称移動の場合は上下が反転することもあります。上下が反転する場合は、 $x^2$ の係数の符号も反転させないといけません。よって、移動後の放物線の方程式は、$x^2$ の係数が $-1$ で、このグラフの頂点が $(1,-2)$ なので\[ y=-(x-1)^2-2 \]となります。これを計算して
\begin{eqnarray} y &=& -(x-1)^2-2 \\ &=& -x^2+2x-3 \\ \end{eqnarray}が答えとなります。ちなみに、原点に関して対称移動する場合も、上下が反転するので、 $x^2$ の係数の符号も反転させないといけません。y に関して対称移動する場合は、上下は反転しないので、 $x^2$ の係数の符号は反転しません。ややこしいですが、グラフをかけば気づくでしょう。

次に、変数の置き換えで解く場合です。

移動前の放物線上の点を $(X,Y)$ とし、この点が対称移動により $(x,y)$ に移動したとします。このとき、移動前は\[ Y=X^2-2X+3 \]を満たしています。また、移動内容から\[ x=X, \ y=-Y \]となります。これを1つ目の式に代入すると
\begin{eqnarray} Y&=&X^2-2X+3 \\ -y&=&x^2-2x+3 \\ y&=&-x^2+2x-3 \\ \end{eqnarray}となります。これが答えです。もちろん、頂点の移動を使った場合と同じ答えです。

なお、y 軸に関して対称移動する場合は、\[ x=-X, \ y=Y \]が成り立つので、移動後の放物線の方程式は\[y=(-x)^2-2(-x)+3\]となります。原点に関して対称移動する場合は、\[ x=-X, \ y=-Y \]が成り立つので、\[-y=(-x)^2-2(-x)+3\]となります。

どちらで解いてもかまいませんが、グラフをかいて符号などが間違っていないか確かめる癖はつけておきましょう。