【標準】2直線の交点とベクトル
ここでは、2直線の交点をベクトルで表す方法を見ていきます。図形とからめたベクトルの問題で、よく出題される内容です。
2直線の交点とベクトル
$\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ とするとき、 $\overrightarrow{ \mathrm{ OP } }$ を $\vec{a}$, $\vec{b}$ を使って表しなさい。
図は次のようになります。
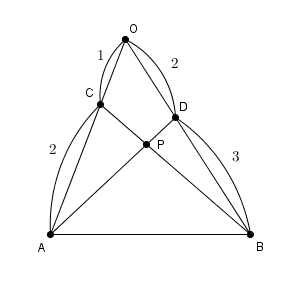
【基本】ベクトルの分解でも見ましたが、 $\vec{a}$, $\vec{b}$ は $\vec{0}$ ではなく平行でもないので、どんなベクトルでもこの2つのベクトルを使って表すことができます。しかも、表し方は1通りであることがわかっています。ただ、この例題のような場合に、具体的にどのように書けるか、まではわかりません。
$\overrightarrow{ \mathrm{ OP } }=x\vec{a}+y\vec{b}$ のような形になるのですが、2つの係数がわかりません。このような「2つのものがわからない」場合、今までの経験から考えると、「2つの式」を作って連立方程式を解けば求められるんじゃないか、と考えられます。
そこで、このベクトルを2通りで表してみましょう。 P を AD 上の点と見る、 BC 上の点と見る、という2つの考え方で表していきます。

P が AD 上の点だ、と言っても、それだけでは式は出てきません。ここでは少し見方を変えて、「 P は AD を内分する点だ」と考えます。【基本】内分点と外分点の位置ベクトルで見たように、 $m:n$ に内分する点の位置ベクトルは\[ \frac{n\vec{u}+m\vec{v} }{m+n} \]という形で書けるんでしたね。ただ、このまま使うと文字が2つになるし、分数が出てきてしまいます。なので、 $s:(1-s)$ とおいて考えていきます。両方を同じ数でかけたり割ったりしても比の内容は変わらないから、このようにおいても構いません。 $1:2$ を $\dfrac{1}{3}:\dfrac{2}{3}$ とおくようなものです。こうすれば、文字が1つになるし、内分点の位置ベクトルの分母が $1$ になって計算が楽になります。
さて、「 P は AD を $s:(1-s)$ に内分する点」だとしましょう。 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$ で、 $\overrightarrow{ \mathrm{ OD } }=\dfrac{2}{5}\vec{b}$ なので、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OP } }
&=&
\frac{(1-s)\overrightarrow{ \mathrm{ OA } }+s\overrightarrow{ \mathrm{ OD } } }{s+(1-s)} \\[5pt]
&=&
(1-s)\vec{a}+\frac{2}{5}s \vec{b} \\[5pt]
\end{eqnarray}となります。
同じようにして、「 P が BC 上にある」と考えて、もう1つ式を作りましょう。「 P は BC を $t:(1-t)$ に内分する点」だと考えると
\begin{eqnarray}
\overrightarrow{ \mathrm{ OP } }
&=&
(1-t)\overrightarrow{ \mathrm{ OB } }+t\overrightarrow{ \mathrm{ OC } } \\[5pt]
&=&
\frac{1}{3}t \vec{a} +(1-t)\vec{b} \\[5pt]
\end{eqnarray}となります。
$\overrightarrow{ \mathrm{ OP } }$ を2通りで表しました。これらは違う表現ですが、 $\vec{a}$, $\vec{b}$ は $\vec{0}$ ではなく平行でもないので、これらは同じものを表しています。つまり、係数は同じです。
そのため、次の連立方程式が成り立ちます。
\begin{eqnarray}
\left\{
\begin{array}{l}
1-s = \dfrac{1}{3}t \\
\dfrac{2}{5}s = 1-t
\end{array}
\right.
\end{eqnarray}
1つ目の式を2つ目に代入して
\begin{eqnarray}
\frac{2}{5}s &=& 1-3(1-s) \\[5pt]
2s &=& 5-15+15s \\[5pt]
13s &=& 10 \\[5pt]
s &=& \frac{10}{13} \\[5pt]
\end{eqnarray}が得られます。1つ目の式に代入すれば
\begin{eqnarray}
t &=& 3(1-s) =\frac{9}{13}
\end{eqnarray}となります。
よって、\[ \overrightarrow{ \mathrm{ OP } }=(1-s)\vec{a}+\frac{2}{5}s \vec{b}=\frac{3}{13}\vec{a}+\frac{4}{13}\vec{b} \]となります。
分解の仕方は1通りなので、違う表現で同じものを2通りで表せば、連立方程式が得られます。これを解いて、分解の仕方を特定する、ということですね。
おわりに
ここでは、2直線の交点をベクトルで表す問題を考えました。流れ自体はそれほど難しくはありませんが、計算のボリュームがあるので、試験などで出題されやすい内容です。





