🏠 Home / 数学II / 図形と方程式 / 領域

【応用】通過領域（存在条件）

🕒 2017/09/24 🔄 2023/05/01

ここでは、直線が動いたときに、その直線が通過する領域を求める問題を、「存在条件」から考える方法で見ていきます。

📘 目次

通過領域

例題1

t がすべての実数値をとって変化するとき、直線 $y=2tx-t^2$ が通過する領域を求めなさい。

【応用】通過領域（縦に切る）と同じ問題ですが、ここでは考え方を変えてみましょう。

上のリンク先の2つ目の例題では、「点 $(2,4)$ を通るような t が存在しないから、この点は通らない」と考えた部分があります。この考えを応用してみましょう。

つまり、「通過する領域にある点が含まれるなら、その点を通る直線があり、対応する t があるはずだ」と考えて、 t の存在する条件を考えていく、という発想です。

直線の式 $y=2tx-t^2$ を t の式だと思って変形すると
\begin{eqnarray} t^2-2xt+y&=&0 \\[5pt] \end{eqnarray}となり、 t の二次方程式だと考えることができます。これを満たす実数 t が存在するのは、判別式が $0$ 以上のときですね（参考：【基本】二次方程式の解の個数と判別式）。よって \begin{eqnarray} (-2x)^2-4y \geqq 0 \\[5pt] y \leqq x^2 \\[5pt] \end{eqnarray}が得られます。これを満たしている点は、 $y=2tx-t^2$ がその点を通るような t が存在するため、「直線を動かしたときに、その点を通る」ということがわかります。

よって、求める領域は次のようになります。

色のついた部分（境界線上の点を含む）となります。

「直線を動かしている」という感じがあまりしない解き方です。

通過領域その２

例題2

t が $t \leqq 1$ を満たすように変化するとき、直線 $y=2tx-t^2$ が通過する領域を求めなさい。

これも、【応用】通過領域（縦に切る）と同じ問題です。上と同じように考えてみましょう。

今回は、 $y=2tx-t^2$ を変形した $t^2-2xt+y=0$ という式が、 $t \leqq 1$ を満たす解を持つ条件を求めればいいですね。少なくとも、実数解は持たなくてはいけないので、先ほど求めた条件 $y \leqq x^2$ を満たす必要があります。

実数解は2つあるかもしれませんが、2つとも $t \leqq 1$ を満たす必要はありません。 $t \leqq 1$ を満たすように直線を動かすのだから、1つでも $t \leqq 1$ を満たしていれば、その点を通ることがわかります。

$t \leqq 1$ となる解を少なくとも1つ持つ条件を考えるには、【応用】二次方程式が実数解を持つ条件（ともにある範囲内）や【応用】二次方程式が実数解を持つ条件（片方正、片方負）で見た内容を使う必要があります。これらにのっとって、判別式、軸、区間の端での値、に注目して考えていきます。

考えないといけない条件は、 $t^2-2xt+y=0$ の解のうち、 $t\leqq 1$ を満たすものが1つ以上ある条件です。イコールを含んでいると考えにくいので、ここでは3つのパターンに分けて考えます。

1. $t=1$ が解となるとき
2. $t\lt 1$ となる解が2つあるとき
3. $t\lt 1$, $t\gt 1$ となる解が1つずつあるとき

まず、1. は、 $t=1$ を代入すると $1-2x+y=0$ だから $y=2x-1$ という条件式が得られます。

2. は、軸が $t=1$ より左にあり、左辺で $t=1$ としたときの値が正になる、という条件になります。軸の条件から $x\lt 1$ が得られ、 $t=1$ での値から $y\gt 2x-1$ となります。

3. は、 $t=1$ としたときの値が負になる、という条件になります。よって、 $y\lt 2x-1$ となります。

実数解を持つ条件 $y \leqq x^2$ は大前提として満たす必要があり、さらに、 1.～3. のどれかを満たす必要があります。これらを加味すると、通過する領域は以下のようになります。

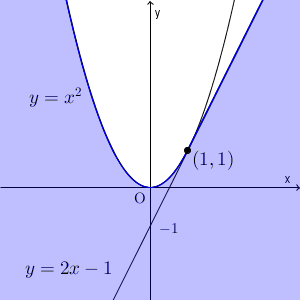
色のついた部分（境界線上の点を含む）となります。

$y=2x-1$ 上の点は、1.より、含まれることがわかります。また、 $y=2x-1$ の左上の部分は、2.より $x\lt 1$ の部分だけが含まれ、 $y=2x-1$ の右下の部分は、3.よりすべて含まれることがわかります。結果として、例題1の答えから、 $y=2x-1$ の左上の部分の $x\gt 1$ のところが除かれることがわかります。

ここでは、3つに分けましたが、逆に「 $t\leqq 1$ を満たすものが1つもない場合」、つまり、「 $t\gt 1$ を満たす解を2つ持つ場合」を除外する、という考えでも構いません。この考えでいくと、実数解を持つ条件 $y \leqq x^2$ から、 $y=2x-1$ の左上の部分の $x\gt 1$ のところが除かれることがわかります。