【基本】一次不等式の解と数直線

ここでは、一次不等式の解を数直線を用いて表現する方法を見ていきます。不等式と数直線については、【基本】不等式の性質と数直線で登場しているので、そちらも参照してみましょう。

解の範囲を数直線を用いて表す

数直線とは、直線上の点と実数とを対応させたものでしたね。一方、一次不等式の解は $x\gt 0$ などといった「範囲」であり、一つの値ではありません。そのため、ちょっとした工夫が必要です。

数直線で「範囲」を示す場合は、次のようにかきます。

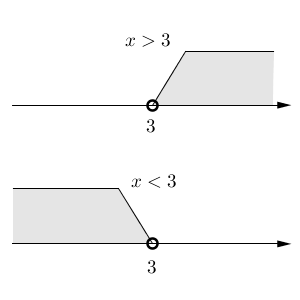
上側の数直線が、$x\gt 3$ 、つまり、3より大きい範囲を示しています。ポイントは、3のところが白丸になっているところです。これで「境目にある"3"は含まない」という意味になります。また、その数を含まない場合は、斜めに線が出るようにかくことが多いです。なお、実際の試験などでは、灰色で塗っている部分は斜線で表現します。

下側の数直線は、$x\lt 3$ を表しています。線の向きが反対になっていますね。

解の範囲を数直線を用いて表す2

$x\gt 3$, $x\lt 3$ のときのかき方を見ましたが、$x\geqq 3$ のように、イコールが入った範囲をかきたい場合もあります。そのときは、次のようにします。

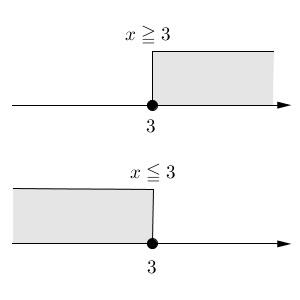
図の上側が $x\geqq 3$ を表していて、下側が $x\leqq 3$ を表しています。ポイントは、3のところが黒丸になっているところです。これにより、「境目の3も含む」という意味になります。また、その数を含む場合は、まっすぐ上に線が出るようにかくことが多いです。

複数の範囲を数直線を用いて表す

数直線を用いて範囲を表す方法を見てきましたが、複数の範囲を示すこともできます。重ねて描くだけです。例えば、$x\gt 0$ と $x\leqq 3$ の両方に含まれる範囲を図示してみましょう。

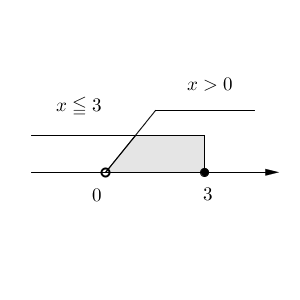
0から右上に出ている線が、$x\gt 0$ を表しています。また、3から上に出て左に伸びている線が、$x\leqq 3$ を表しています。この2つの領域は重なる部分があって、それが灰色の部分であることがわかりますね。式で書くと、$0 \lt x \leqq 3$ となります。

おわりに

数直線を用いて範囲を表す方法を見てきました。範囲の端を含まない場合は白丸にする、端を含む場合は黒丸にする、というのがポイントでしたね。

範囲が一つだけならあまりありがたみが感じられませんが、複数の範囲を考えるようになると、数直線で考えたほうがわかりやすくなります。複数の範囲が出てきて複雑だなぁと感じた場合は、数直線を用いて考えるようにしましょう。