京都大学 文系 2016年度 第1問 解説
問題編
【問題】
xy平面内の領域\[x^2+y^2 \leqq 2, \quad |x|\leqq 1\]で、曲線$C:y=x^3+x^2-x$の上側にある部分の面積を求めよ。
【考え方】
見た目はめんどそうな問題ですが、関数の形を調べていくとなかなかいい形になっています。
円の形はすぐにわかるので、まずは三次関数の形を調べるところから着手します。円とどう交わっているかによって話が変わってくるからです。微分して増減表を書くと、円とは2点でしか交わらないことがわかります。また、その2点もきれいな値になります。
考える領域は、きれいに2つにわけることができます。片方は積分、片方は図形的に計算します。
解答編
【問題】
xy平面内の領域\[x^2+y^2 \leqq 2, \quad |x|\leqq 1\]で、曲線$C:y=x^3+x^2-x$の上側にある部分の面積を求めよ。
【解答】
$f(x)=x^3+x^2-x$とする。
よって、面積を求める領域は、下の図の色のついた部分となる。
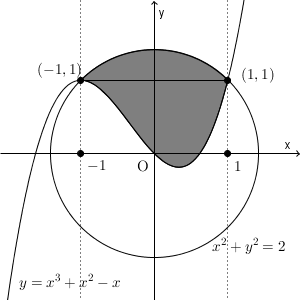
この領域を$y=1$で切り2つに分ける。下側の面積は、
\begin{eqnarray}
& &
\int_{-1}^ 1 \{ 1 - (x^3+x^2-x) \} dx \\
&=&
\int_{-1}^ 1 \{ 1 - x^3 - x^2 + x) \} dx \\
&=&
\left[ x-\frac{x^4}{4} - \frac{x^3}{3} +\frac{x^2}{2} \right]_{-1}^ 1 \\
&=&
2-\frac{2}{3} = \frac{4}{3}
\end{eqnarray}となる。
上側の面積は、中心角が90度の扇形から三角形をひいて求めると、
\begin{eqnarray}
\sqrt{2}\sqrt{2}\pi\frac{1}{4} - \frac{1}{2}\sqrt{2}\sqrt{2}
&=&
\frac{\pi}{2}-1
\end{eqnarray}となる。
以上から、求める面積は、\[ \frac{4}{3} + \frac{\pi}{2}-1 = \frac{\pi}{2}+\frac{1}{3} \]となる。
【解答終】
【解説】
$-1\lt x \lt 1$のとき、下の図のように、三次関数が円の下側に行ってないかどうかをチェックすることは必要です。
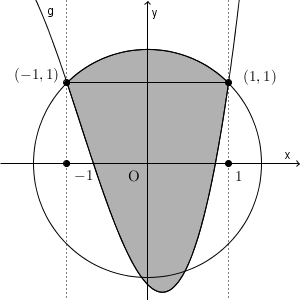
もし下側に突き抜けていた場合は、円より下の部分は除外して答えないといけません。
求める領域を2つに分けて上側の面積を出すときに、「扇形から三角形を引く」方法を使いました。この方法は入試でよく使うので、すぐに思いつけるようにしておきましょう。





