センター試験 数学II・数学B 2014年度追試 第5問 解説
【選択問題】(第3問~第6問から2問選択)
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$ある自動車の4月21日から4月30日までの毎日の走行距離とガソリンの消費量を調べたところ、次のデータが得られた。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
以下、小数の形で解答する場合、指定された桁数の一つ下の桁を四捨五入し、解答せよ。途中で割り切れた場合、指定された桁まで 0 にマークすること。
日付 走行距離
(km)消費量
(リットル)4月21日 18.0 1.2 4月22日 17.0 1.1 4月23日 17.5 1.4 4月24日 20.0 1.3 4月25日 19.5 1.2 4月26日 19.0 1.5 4月27日 18.0 1.0 4月28日 19.5 1.3 4月29日 20.5 1.7 4月30日 21.0 1.3 平均値 $\mathsf{A}$ 1.30 分散 1.60 $\mathsf{B}$ (1) この自動車の4月21日から4月30日までの走行距離の平均値 $\mathsf{A}$ は $\myBox{アイ}.\myBox{ウエ}$ km である。また、ガソリンの消費量の分散 $\mathsf{B}$ の値は $\myBox{オ}.\myBox{カキク}$ であり、中央値は $\myBox{ケ}.\myBox{コサ}$ リットルである。
(2) 走行距離とガソリンの消費量の相関図(散布図)として適切なものは $\myBox{シ}$ であり、相関係数の値は $\myBox{ス}.\myBox{セソタ}$ である。ただし、 $\myBox{シ}$ については、当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
(3) さらに、同じ自動車について、5月1日から5月6日までの毎日の走行距離とガソリンの消費量を調べたところ、次のデータが得られた。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
日付 走行距離
(km)消費量
(リットル)5月1日 20.5 1.6 5月2日 25.5 1.8 5月3日 22.0 1.3 5月4日 22.5 1.8 5月5日 20.5 1.6 5月6日 27.0 2.1 平均値 23.00 1.70 分散 6.00 0.060 5月1日から5月6日までの6日間の走行距離とガソリンの消費量の相関係数の値は0.750である。また、4月21日から5月6日までの16日間の走行距離とガソリンの消費量の相関係数の値を r とする。16日間の相関図を考えることにより、 $\myBox{チ}$ である。 $\myBox{チ}$ にあてはまるものを、次の 0 から 6 のうちから一つ選べ。
0: $r\lt -1$
1: $r=-1$
2: $-1 \lt r \lt 0$
3: $r=0$
4: $0 \lt r \lt 1$
5: $r=1$
6: $r\gt 1$次に、この自動車の4月21日から5月6日までの16日間の走行距離の平均値と分散の値について考えよう。16日間の平均値を M とするとき、 M は $\myBox{ツテ}.\myBox{トナ}$ kmである。
4月21日から4月30日までの走行距離を順に $x_1, x_2, \cdots, x_{10}$ とおき、これらの平均値を m、分散の値を $s^2$ とする。また\[ T=(x_1-M)^2+(x_2-M)^2+\cdots+(x_{10}-M)^2 \]を考える。 k を 1 から 10 までの自然数として $(x_k-M)^2$ は
\begin{eqnarray} (x_k-M)^2 &=& \{ (x_k-m)+(m-M) \}^2 \\ &=& (x_k-m)^2+2(x_k-m)(m-M)+(m-M)^2 \\ \end{eqnarray}と変形できるから\[ T=\myBox{ニ} \]と表すことができる。 $\myBox{ニ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。0: $10s^2 +10(m-M)^2$
1: $20s^2 +10(m-M)^2$
2: $10s^2 +20(m-M)^2$
3: $20s^2 +20(m-M)^2$したがって、 $T=\myBox{ヌネ}.\myBox{ノハ}$ である。さらに、5月1日から5月6日までの走行距離についても、同様の計算を行うことにより、16日間の走行距離の分散の値は $\myBox{ヒ}.\myBox{フヘ}$ であることが導かれる。
考え方
(1)は定義に基づいて計算するだけです。(2)の散布図は、違う点を探して比較しましょう。相関係数は少し計算が面倒ですが、地道に求めるしかありません。(3)は散布図がどういう形になるかを考えて答えましょう。計算は必要ありません。
ここまでは基本的で簡単な問題が続きますが、最後の16日間の分散の箇所だけ少し難易度が上がります。 T の式を変形する部分は、ヒントにある変形式の各項の和がどうなるかを考えましょう。また、 $s^2$ が分散なので、代入するときに間違って2乗をしないようにしましょう。
【選択問題】(第3問~第6問から2問選択)
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$ある自動車の4月21日から4月30日までの毎日の走行距離とガソリンの消費量を調べたところ、次のデータが得られた。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
以下、小数の形で解答する場合、指定された桁数の一つ下の桁を四捨五入し、解答せよ。途中で割り切れた場合、指定された桁まで 0 にマークすること。
日付 走行距離
(km)消費量
(リットル)4月21日 18.0 1.2 4月22日 17.0 1.1 4月23日 17.5 1.4 4月24日 20.0 1.3 4月25日 19.5 1.2 4月26日 19.0 1.5 4月27日 18.0 1.0 4月28日 19.5 1.3 4月29日 20.5 1.7 4月30日 21.0 1.3 平均値 $\mathsf{A}$ 1.30 分散 1.60 $\mathsf{B}$ (1) この自動車の4月21日から4月30日までの走行距離の平均値 $\mathsf{A}$ は $\myBox{アイ}.\myBox{ウエ}$ km である。また、ガソリンの消費量の分散 $\mathsf{B}$ の値は $\myBox{オ}.\myBox{カキク}$ であり、中央値は $\myBox{ケ}.\myBox{コサ}$ リットルである。
解説
走行距離の平均値を求めます。仮平均を18とすると、この仮平均からの差を足し合わせたものは
\begin{eqnarray}
& & 0 +(-1 )+(-0.5) +2 +1.5 \\
& & +1 +0 +1.5 +2.5 +3 \\
&=&
10 \\
\end{eqnarray}となるので、平均値は\[ 18+\frac{10}{10}=19.00 \]となります。
ガソリンの消費量の分散を求めるために、各値の平均値との差の2乗の和を計算します。
\begin{eqnarray}
& & (-0.1)^2 +(-0.2)^2 +0.1^2 +0^2 +(-0.1)^2 \\
& & +0.2^2 +(-0.3)^2 +0^2 +0.4^2 +0^2 \\
&=&
0.01 +0.04 +0.01 +0.01 +0.04 +0.09 +0.16 \\
&=&
0.36 \\
\end{eqnarray}となります。これを個数10でわったものが分散なので、分散は\[ \frac{0.36}{10}=0.036 \]となります。
ガソリン消費量の中央値を求めるには、まず値を小さい順に並べます。
\begin{eqnarray}
1.0, \ 1.1, \ 1.2, \ 1.2, \ 1.3, \ 1.3, \ 1.3, \ 1.4, \ 1.5, \ 1.7
\end{eqnarray}となります。データの数が10個なので、5番目と6番目の平均が中央値となります。よって\[ \frac{1.3+1.3}{2}=1.30 \]となります。
解答
アイウエ:1900
オカキク:0036
ケコサ:130
参考
解答編 つづき
問題
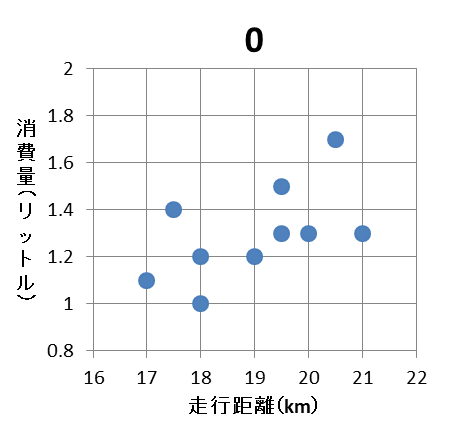
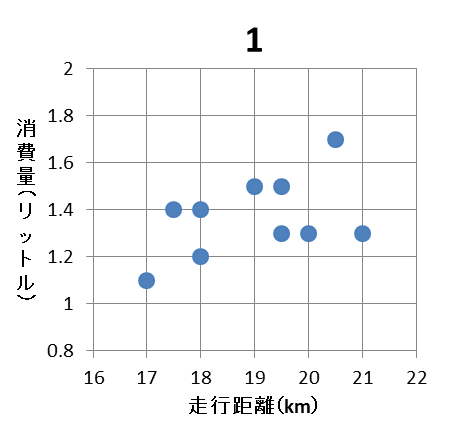
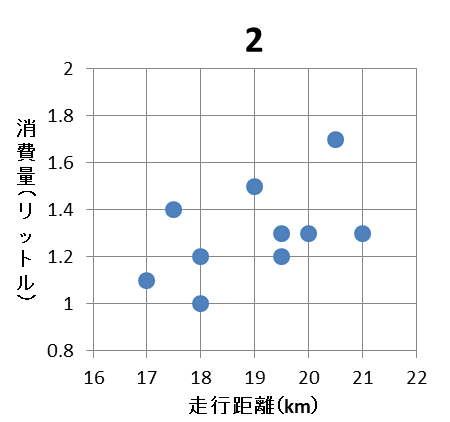
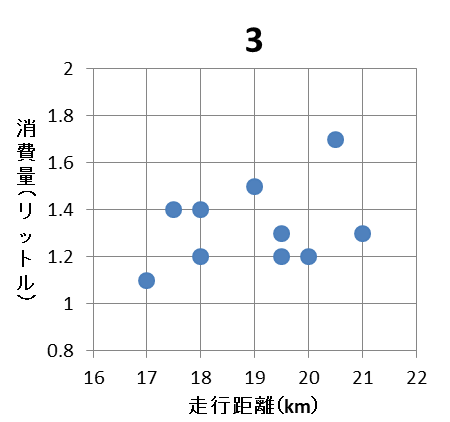
(2) 走行距離とガソリンの消費量の相関図(散布図)として適切なものは $\myBox{シ}$ であり、相関係数の値は $\myBox{ス}.\myBox{セソタ}$ である。ただし、 $\myBox{シ}$ については、当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
解説
散布図は、各選択肢を比べて違う点を探し、消去法で考えていきましょう。
散布図の左側から順番に見ていくと、走行距離が18kmの点で違いがあります。表を見ると、消費量は1.2と1.0なので、1と3の選択肢は間違っていることがわかります。
次に、0と2で違う点を探しましょう。すると、走行距離19kmの点で違いがあります。消費量は1.5なので、0ではないことがわかります。
以上から、2と求められます。
相関係数は、共分散をそれぞれの標準偏差で割ったものです。標準偏差は分散の平方根なので、表とオカキクの結果からわかります。共分散を求めましょう。
共分散は、偏差(平均からの差)の積を足して、個数で割ったものです。偏差の積は次のようになります。
| 日付 | 走行距離 偏差 | 消費量 偏差 | 偏差の積 |
| 4月21日 | -1 | -0.1 | 0.1 |
| 4月22日 | -2 | -0.2 | 0.4 |
| 4月23日 | -1.5 | 0.1 | -0.15 |
| 4月24日 | 1 | 0 | 0 |
| 4月25日 | 0.5 | -0.1 | -0.05 |
| 4月26日 | 0 | 0.2 | 0 |
| 4月27日 | -1 | -0.3 | 0.3 |
| 4月28日 | 0.5 | 0 | 0 |
| 4月29日 | 1.5 | 0.4 | 0.6 |
| 4月30日 | 2 | 0 | 0 |
\begin{eqnarray} & & \frac{0.1 +0.4 -0.15 +0 -0.05 +0 +0.3 +0 +0.6 +0}{10} &=& \frac{1.2}{10} &=& 0.12 \end{eqnarray}となります。これが共分散の値です。これから、相関係数は \begin{eqnarray} \frac{0.12}{\sqrt{1.6}\sqrt{0.036} } &=& \frac{12}{\sqrt{16}\sqrt{36} } \\[5pt] &=& \frac{12}{24} \\[5pt] &=& 0.500 \end{eqnarray}と求められます。
解答
シ:2
スセソタ:0500
参考
解答編 つづき
問題
(3) さらに、同じ自動車について、5月1日から5月6日までの毎日の走行距離とガソリンの消費量を調べたところ、次のデータが得られた。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
日付 走行距離
(km)消費量
(リットル)5月1日 20.5 1.6 5月2日 25.5 1.8 5月3日 22.0 1.3 5月4日 22.5 1.8 5月5日 20.5 1.6 5月6日 27.0 2.1 平均値 23.00 1.70 分散 6.00 0.060 5月1日から5月6日までの6日間の走行距離とガソリンの消費量の相関係数の値は0.750である。また、4月21日から5月6日までの16日間の走行距離とガソリンの消費量の相関係数の値を r とする。16日間の相関図を考えることにより、 $\myBox{チ}$ である。 $\myBox{チ}$ にあてはまるものを、次の 0 から 6 のうちから一つ選べ。
0: $r\lt -1$
1: $r=-1$
2: $-1 \lt r \lt 0$
3: $r=0$
4: $0 \lt r \lt 1$
5: $r=1$
6: $r\gt 1$
解説
4月21日から30日までのデータでは相関係数が正であり、5月1日から6日までのデータでも相関係数が正です。どちらも、散布図が右肩上がり、というデータなので、これらを混ぜても、やはり散布図は右肩上がりとなります。よって、選択肢の4か5にしぼられます。
選択肢5は、散布図で見たときに、各点が一直線上にないといけませんが、今のデータではそんなことは起こりません。4月21日から30日までの散布図を見るとわかります。以上から、16日間の相関係数は $0\lt r \lt 1$ となります。
なお、相関係数の絶対値は1以下なので、選択肢の0や6は絶対に起こりません。
解答
チ:4
参考
解答編 つづき
問題
次に、この自動車の4月21日から5月6日までの16日間の走行距離の平均値と分散の値について考えよう。16日間の平均値を M とするとき、 M は $\myBox{ツテ}.\myBox{トナ}$ kmである。
解説
16日間の走行距離の平均値を求めるには、16日間の走行距離の和を16で割れば求められます。
前半10日間の走行距離の和は、平均値に10を掛ければ求められます。また、後半6日間の走行距離の和は、平均値に6を掛ければ求められます。よって、16日間の走行距離の平均値は、
\begin{eqnarray}
\frac{19\times 10 + 23\times 6}{16}
&=&
\frac{328}{16} \\[5pt]
&=&
20.50
\end{eqnarray}と求められます。
解答
ツテトナ:2050
参考
解答編 つづき
問題
4月21日から4月30日までの走行距離を順に $x_1, x_2, \cdots, x_{10}$ とおき、これらの平均値を m、分散の値を $s^2$ とする。また\[ T=(x_1-M)^2+(x_2-M)^2+\cdots+(x_{10}-M)^2 \]を考える。 k を 1 から 10 までの自然数として $(x_k-M)^2$ は
\begin{eqnarray} (x_k-M)^2 &=& \{ (x_k-m)+(m-M) \}^2 \\ &=& (x_k-m)^2+2(x_k-m)(m-M)+(m-M)^2 \\ \end{eqnarray}と変形できるから\[ T=\myBox{ニ} \]と表すことができる。 $\myBox{ニ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。0: $10s^2 +10(m-M)^2$
1: $20s^2 +10(m-M)^2$
2: $10s^2 +20(m-M)^2$
3: $20s^2 +20(m-M)^2$したがって、 $T=\myBox{ヌネ}.\myBox{ノハ}$ である。さらに、5月1日から5月6日までの走行距離についても、同様の計算を行うことにより、16日間の走行距離の分散の値は $\myBox{ヒ}.\myBox{フヘ}$ であることが導かれる。
解説
文章中にある式\[ (x_k-M)^2 = (x_k-m)^2+2(x_k-m)(m-M)+(m-M)^2 \]で、左辺を $k=1$ から $k=10$ まで足したものが T となります。このとき、右辺がどうなるか考えてみましょう。
まず、1項目は\[ (x_1-m)^2+(x_2-m)^2+\cdots+(x_{10}-m)^2 \]となります。これを個数10で割ったものが分散になるので、この値は $10s^2$ となります。
2項目は
\begin{eqnarray}
& &
2(x_1-m)(m-M)+2(x_2-m)(m-M)+\cdots+2(x_{10}-m)(m-M) \\
&=&
2(m-M)\{ (x_1-m)+(x_2-m)+\cdots+(x_{10}-m)\} \\
&=&
2(m-M)\{ x_1+x_2+\cdots+x_{10} -10m\} \\
\end{eqnarray}となります。 m は平均なので、波かっこの中は $0$ となるため、2項目は $0$ になることがわかります。
3項目は $(m-M)^2$ を10回足すことになるので $10(m-M)^2$ となります。
以上から\[ T=10s^2+10(m-M)^2 \]が成り立つことがわかります。
$s^2$ は分散なので $6$, $m$ は10日間の平均なので $19$, $M$ は16日間の平均なので $20.5$ だから、これらを代入して
\begin{eqnarray}
T
&=&
10 \times 1.6 +10(19-20.5)^2 \\
&=&
16 +22.5 \\
&=&
38.50 \\
\end{eqnarray}と求められます。
同様に考えると、5月1日から6日までの走行距離について、偏差の2乗の和を計算した結果は
\begin{eqnarray}
& &
6 \times 6 +6(23-20.5)^2 \\
&=&
36 +37.5 \\
&=&
73.5 \\
\end{eqnarray}となります。
よって、16日間の走行距離の分散の値は
\begin{eqnarray}
\frac{38.5+73.5}{16} = \frac{112}{16} = 7.00
\end{eqnarray}と求められます。
解答
ニ:0
ヌネノハ:3850
ヒフヘ:700