【標準】二次曲線の極方程式
ここでは、二次曲線の極方程式を見ていきます。
放物線の極方程式
まずは放物線の極方程式を見ていきます。
点 $\mathrm{A}(a,0)$ を通り、始線に垂直な直線を $\ell$ とします。 $\ell$ からの距離と極 $\mathrm{O}$ からの距離が等しくなる場合を考えましょう。つまり、 $\mathrm{O}$ を焦点、 $\ell$ を準線とする放物線を考える、ということです。
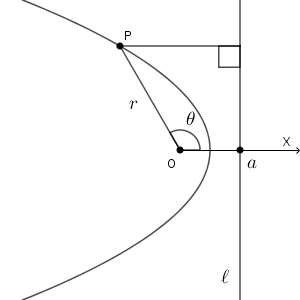
放物線上の点 $\mathrm{P}(r,\theta)$ をとります。 $\mathrm{O}$ からの距離は、もちろん $r$ です。 準線からの距離は $a-r\cos\theta$ となります。よって
\begin{eqnarray}
r &=& a-r\cos\theta \\[5pt]
r(1+\cos\theta) &=& a \\[5pt]
r &=& \frac{a}{1+\cos\theta} \\[5pt]
\end{eqnarray}となります。これが放物線の極方程式です。
なので、例えば、\[ r=\frac{1}{1+\cos\theta} \]は、 $(1,0)$ を通り、始線に垂直な直線を準線とし、極 $\mathrm{O}$ を焦点とする放物線の極方程式、となります。
楕円の極方程式
次の問題を考えてみましょう。
先ほどの放物線の式とよく似ていますが、分母の $1$ のところが $2$ になっています。ここが変わるとどうなるでしょうか。
極方程式から直交座標に変換するには、 $r=\sqrt{x^2+y^2}$ や $x=r\cos\theta$ などの関係式を使えばいいです(参考:【基本】極座標)。整理すると、次のようになります。
\begin{eqnarray}
r(2+\cos\theta) &=& 1 \\[5pt]
2r+x &=& 1 \\[5pt]
2r &=& 1-x \\[5pt]
4r^2 &=& (1-x)^2 \\[5pt]
4(x^2+y^2) &=& x^2-2x+1 \\[5pt]
3x^2+2x+4y^2 &=& 1 \\[5pt]
3\left(x+\frac{1}{3}\right)^2-\frac{1}{3}+4y^2 &=& 1 \\[5pt]
3\left(x+\frac{1}{3}\right)^2+4y^2 &=& \frac{4}{3} \\[5pt]
\frac{9}{4}\left(x+\frac{1}{3}\right)^2+3y^2 &=& 1 \\[5pt]
\end{eqnarray}となります。楕円の方程式ですね。
実は、\[ r=\frac{ea}{1+e\cos\theta} \]という極方程式は、二次曲線を表すことが知られています。ここで、 $e$ は離心率といって、値によって以下のようになります。
- $0\lt e\lt 1$ のとき、楕円を表す。焦点の1つは極 $\mathrm{O}$ である。
- $e=1$ のとき、放物線を表す。焦点は極 $\mathrm{O}$ である。
- $e\gt 1$ のとき、双曲線を表す。焦点の1つは極 $\mathrm{O}$ である。
このページでは、前半で放物線を扱いました。後半では楕円を扱いましたが、これは $e=\dfrac{1}{2}$ の場合に対応しています。詳しくは、【応用】二次曲線の極方程式 で取り上げます。
おわりに
ここでは、二次曲線の極方程式について見てきました。放物線や楕円の具体例を見ました。一般的な話は、【応用】二次曲線の極方程式 で取り上げます。





