【標準】二次関数の最大・最小(上下に動く)
二次関数の最大値と最小値の求め方について、定義域が実数全体の場合と定義域に制限のある場合の2つの場合を見てきました。ここからは、二次関数の係数や定義域に別の文字が入ってきて、二次関数や定義域が動く場合を見ていきます。話がややこしくて多くの人がつまづくので、入試などでもよく問われる内容になっています。
上下に動く場合
この記事では、定数項に文字が入っている場合を考えます。
定数項に文字が入っていますが、まずは、文字が入ったままの状態で最小値を求めることを考えましょう。
グラフをかくために、平方完成をして次のように変形します。
\begin{eqnarray}
y
&=&
-x^2+3x+c+1 \\
&=&
-(x^2-3x)+c+1 \\
&=&
-\left( x-\frac{3}{2} \right)^2 +\frac{9}{4} +c+1 \\
&=&
-\left( x-\frac{3}{2} \right)^2 +c+\frac{13}{4} \\
\end{eqnarray}このことから、グラフは次のようになります。
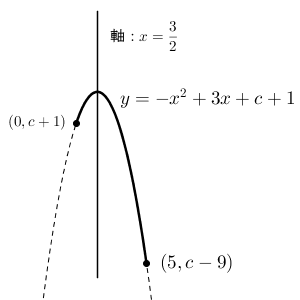
今までに見たグラフとかなり違っています。 c の値がわからないので、 x 軸との関係がわかりません。そのため、$x$ 軸や $y$ 軸を省略しています。かわりに、放物線の軸をかいています。放物線の軸は、上の平方完成した式からわかりますね。
この関数の $x^2$ の係数は負なので、上に凸のグラフです。放物線の軸から離れれば離れるほどグラフ上の点は下に行くので、区間の左端より右端の方が下にあります。よって、グラフから、この関数の最小値は $y=c-9$ ( $x=5$ のとき)となることがわかります。
条件から、最小値が $-1$ になるということなので、 $c-9=-1$ から $c=8$ と求められます。これが答えです。
c の値が大きくても小さくても、定義域の右端で最小となることに変わりはありません。少し変わったグラフになりますが、形状が分かるようにグラフをかいて考えましょう。
おわりに
ここでは、二次関数の定数項の部分に別の文字が入っている例を見ました。この文字の値によって、二次関数のグラフは上下に移動することになります。上下方向だけの移動ならまだ考えやすいですが、今後はもう少し複雑な状況も考えていくことになります。





