【標準】同一直線上にある3点と空間ベクトル
ここでは、「3点が同一直線上にあること」の証明に、ベクトルを使う方法を見ていきます。
同一直線上にある3点
【標準】同一直線上にある3点とベクトル で見たように、異なる3点 $\mathrm{A,B,C}$ が同一直線上にあることは、 $\overrightarrow{\mathrm{AC}}=k \overrightarrow{\mathrm{AB}}$ を満たす $k$ が存在することと同値でした。これは、空間の世界でも成り立ちます。
$\overrightarrow{\mathrm{AC}}=k \overrightarrow{\mathrm{AB}}$ と表せることは、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が平行であることと同値です(参考:【基本】空間ベクトルの平行と分解)。また、どちらも点 $\mathrm{A}$ を通っているのだから、3点 $\mathrm{A,B,C}$ は同一直線上にあることがわかります。
3点が同一直線上にあることを示すのは難しいことが多いです。特に、空間の世界では、図をかくのも大変で、イメージしにくいです。そのため、計算で考えることができるベクトルは、強い武器になります。
例題1
ベクトルが出てきていませんが、ベクトルで考えてみます。成分を考えると
\begin{eqnarray}
\overrightarrow{\mathrm{AB}} &=& (-5,-3,7)-(1,1,3) \\[5pt]
&=& (-6,-4,4) \\[5pt]
\overrightarrow{\mathrm{AC}} &=& (p,q,0)-(1,1,3) \\[5pt]
&=& (p-1,q-1,-3)
\end{eqnarray}となります。3点が同一直線上にあることは\[ (p-1,q-1,-3)=k(-6,-4,4) \]を満たす $k$ が存在することと同値です。 $z$ 成分より\[ k=-\dfrac{3}{4} \]とわかるので
\begin{eqnarray}
p-1 &=& -6k \\[5pt]
p &=& -6\cdot \left(-\frac{3}{4}\right)+1 = \frac{11}{2} \\[5pt]
q-1 &=& -4k \\[5pt]
q &=& -4\cdot \left(-\frac{3}{4}\right)+1 = 4
\end{eqnarray}と求められます。
なお、 $\mathrm{C}$ の $z$ 成分が $0$ であることから、この問題は、直線 $\mathrm{AB}$ と $xy$ 平面との交点の座標を求めていた、と考えることもできます。
例題2
(1) $\mathrm{ST}$ と $\mathrm{UV}$ は1点で交わることを示しなさい。
(2) (1)の交点を $\mathrm{W}$ とし、三角形 $\mathrm{ABC}$ の重心を $\mathrm{G}$ とする。3点 $\mathrm{O,W,G}$ が同一直線上にあることを示しなさい。
正四面体ならまだ考えやすいですが、この問題は正四面体とはいってません。一般の四面体で考えます。
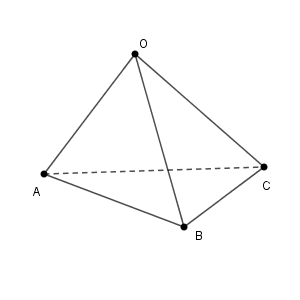
ベクトルが出てきていませんが、ベクトルを使って考えていきましょう。 $\overrightarrow{\mathrm{OA}}=\vec{a}$, $\overrightarrow{\mathrm{OB}}=\vec{b}$, $\overrightarrow{\mathrm{OC}}=\vec{c}$ とします。
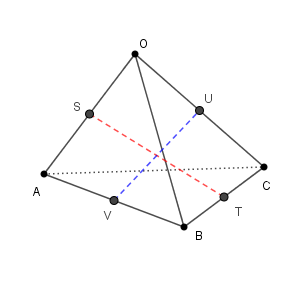
こうすると、(1)の $\mathrm{S,T,V,U}$ については、
\begin{eqnarray}
\overrightarrow{\mathrm{OS}} &=& \frac{1}{2}\vec{a} \\[5pt]
\overrightarrow{\mathrm{OT}} &=& \frac{1}{2}\vec{b}+\frac{1}{2}\vec{c} \\[5pt]
\overrightarrow{\mathrm{OU}} &=& \frac{1}{2}\vec{c} \\[5pt]
\overrightarrow{\mathrm{OV}} &=& \frac{1}{2}\vec{a}+\frac{1}{2}\vec{b} \\[5pt]
\end{eqnarray}となります。このことから、 $\mathrm{ST}$ の中点も、 $\mathrm{UV}$ の中点も、どちらの位置ベクトルも\[ \frac{1}{4}\vec{a}+\frac{1}{4}\vec{b}+\frac{1}{4}\vec{c} \]となることがわかります。位置ベクトルが一致するので、点も一致することがわかります。
続いて、(2)を考えます。
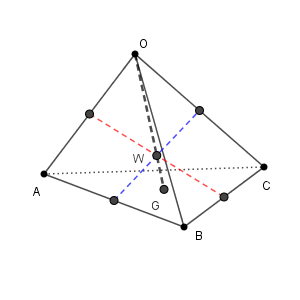
先ほどの結果から\[ \overrightarrow{\mathrm{OW}}=\frac{\vec{a}+\vec{b}+\vec{c}}{4} \]となることがわかります。また、三角形の重心の座標の位置ベクトルは、頂点の位置ベクトルを足して3で割ればいいので(参考:【基本】空間における位置ベクトル)\[ \overrightarrow{\mathrm{OG}}=\frac{\vec{a}+\vec{b}+\vec{c}}{3} \]です。
こうして、\[ \overrightarrow{\mathrm{OG}}=\frac{4}{3}\overrightarrow{\mathrm{OW}} \]となることがわかるので、3点 $\mathrm{O,W,G}$ が同一直線上にあることが示せました。
おわりに
ここでは、空間内で3点が同一直線上にあることを示すために、ベクトルを使う例を見ました。ベクトルの計算だけで進めていけるので、図をかきにくい空間の問題では威力を発揮します。





