【発展】ユークリッドの互除法と連分数
ここでは、ユークリッドの互除法と関連のある連分数について紹介します。入試で扱われることは少ないですが、こういう応用例を知っておくのも悪くないでしょう。特に、 $\sqrt{2}$ の連分数展開はインパクトがあるので、結果だけでも見ておくとおもしろいです。
連分数
ユークリッドの互除法を説明する際、【基本】ユークリッドの互除法の使い方では、「 $1649$ と $221$ の最大公約数」を例に用いて、次のような計算をしていました。
\begin{eqnarray}
1649 &=& 221 \times 7 + 102 \\
221 &=& 102 \times 2 + 17 \\
102 &=& 17 \times 6 \\
\end{eqnarray}少し形が変わっていますが、ほとんど同じ内容です。
さて、上の式を、右辺の1つ目の数字でそれぞれ割ってみましょう。すると、次のようになります。
\begin{eqnarray}
\frac{1649}{221} &=& 7 + \frac{102}{221} \\[5pt]
\frac{221}{102} &=& 2 + \frac{17}{102} \\[5pt]
\frac{102}{17} &=& 6 \\[5pt]
\end{eqnarray}ここで注目したいのが、左辺の逆数が、上の式の右辺の2項目になっているということです。そのため、3つ目の式を2つ目に代入すると、次のようになります。
\begin{eqnarray}
\frac{221}{102} &=& 2 + \frac{1}{6} \\[5pt]
\end{eqnarray}さらにこれを1つ目の式に代入すると、次のようになります。
\begin{eqnarray}
\frac{1649}{221} &=& 7 + \frac{1}{2 + \frac{1}{6} } \\[5pt]
\end{eqnarray}分母に分数が出てきました。このように、分母に分数が含まれているような分数のことを連分数(continued fraction) といいます。各分数の分子が $1$ になっているものを正則連分数といいますが、単に「連分数」といっただけで「正則連分数」を指すこともあります。
ユークリッドの互除法と連分数
上で出てきた $\displaystyle \frac{1649}{221}$ という分数は連分数の形で書けましたが、これはたまたまではありません。どんな有理数も、連分数で書くことができます。手順は、ユークリッドの互除法と同じ流れです。
例えば、 $\displaystyle \frac{r_0}{r_1}$ という有理数を考えましょう($r_0$, $r_1$ は自然数)。 $r_0$ を $r_1$ で割った商を $q_1$ 、余りを $r_2$ とすると
\begin{eqnarray}
\frac{r_0}{r_1}=q_1+\frac{r_2}{r_1}
\end{eqnarray}と書けます。 $r_1$ を $r_2$ で割った商を $q_2$ 、余りを $r_3$ とすれば
\begin{eqnarray}
\frac{r_1}{r_2}=q_2+\frac{r_3}{r_2}
\end{eqnarray}なので、これの逆数を考えて上の式に入れると
\begin{eqnarray}
\frac{r_0}{r_1}=q_1+\frac{1}{ \displaystyle q_2+\frac{r_3}{r_2} }
\end{eqnarray}となります。 $r_2$ を $r_3$ で割った商を $q_3$ 、余りを $r_4$ とすれば
\begin{eqnarray}
\frac{r_2}{r_3}=q_3+\frac{r_4}{r_3}
\end{eqnarray}なので、これをもう一度上の式に入れると
\begin{eqnarray}
\frac{r_0}{r_1}=q_1+\frac{1}{ \displaystyle q_2+\frac{1}{ \displaystyle q_3+\frac{r_4}{r_3} }}
\end{eqnarray}となります。
このように、新しく分母に出てくる分数を置き換えていく操作を繰り返していけば、いつかは終わります。計算が進むたびに余りはどんどん小さくなっていくからです。しかも、逆数にして代入していくので、各分子はすべて $1$ になります。結局、次のような形で表せることがわかります。
\begin{eqnarray}
\frac{r_0}{r_1}=q_1+\frac{1}{ \displaystyle q_2+\frac{1}{ \displaystyle \ddots q_{n-1}+\frac{1}{q_n} }}
\end{eqnarray}このようにして、有理数は有限段の連分数の形で書けることがわかります。このように連分数の形で書くことを「連分数展開をする」といいます。
また、計算をしていけば、逆に有限段の連分数が有理数で書けることもわかります。
ルート2の連分数展開
「有理数は有限段の連分数の形で書ける」と書きましたが、では、無理数の場合はどうなるでしょうか。以下では、 $\sqrt{2}$ を使って考えてみましょう。
突然ですが、次の式を考えてみます。\[ 1+\frac{1}{1+\sqrt{2} } \]この値は、次のようにして求めることができます。
\begin{eqnarray}
1+\frac{1}{1+\sqrt{2} }
&=&
1+\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)} \\[5pt]
&=&
1+\sqrt{2}-1 \\[5pt]
&=&
\sqrt{2} \\[5pt]
\end{eqnarray}つまり、次の式が成り立ちます。\[ \sqrt{2}=1+\frac{1}{1+\sqrt{2} } \]さて、ここからこの式を使って少し変わったことをしてみます。この式の右辺にある $\sqrt{2}$ にこの式を代入してみます。すると、次のような式があらわれます。
\begin{eqnarray}
\sqrt{2}=1+\frac{1}{ \displaystyle 1+\left(1+\frac{1}{1+\sqrt{2} }\right)}
\end{eqnarray}連分数チックになりました。 $\sqrt{2}$ が残っているので、連分数ではなく、連分数「チック」です。さらにもう一度代入してみましょう。
\begin{eqnarray}
\sqrt{2}=1+\frac{1}{ \displaystyle 1+1+\frac{1}{ \displaystyle 1+1+\frac{1}{1+\sqrt{2} }} }
\end{eqnarray}さらに、連分数チックになりました。ただし、上で見たユークリッドの互除法のときとは異なり、右辺の $\sqrt{2}$ が消えることはありません。なので、この式は次のように無限に続いていきます。
\begin{eqnarray}
\sqrt{2}=1+\frac{1}{ \displaystyle 2+\frac{1}{ \displaystyle 2+\frac{1}{ 2+\ddots } }}
\end{eqnarray}実はこれが、 $\sqrt{2}$ の連分数表示となります。厳密さを欠いた説明ですが、次のように考えてみましょう。
\begin{eqnarray}
x=1+\frac{1}{ \displaystyle 1+1+\frac{1}{ \displaystyle 1+1+\frac{1}{ 1+1+\ddots } }}
\end{eqnarray}とおくと、 x は\[ x=1+\frac{1}{1+x} \]を満たさないといけません(分母に出てくる分数をよく見て対応を考えましょう)が、 $\sqrt{2}$ はこの解になっていて、正の解はこれだけです。なので、上の連分数は $\sqrt{2}$ となります。
ただ、これだけを見ても、この連分数はただ気持ち悪いだけで、何の役に立つのかよくわかりません。しかし、これから述べるように $\sqrt{2}$ の近似値を計算するのに役に立ちます。
上で使った次の式\[ \sqrt{2}=1+\frac{1}{1+\sqrt{2} } \]を応用して、次のような数列を考えてみましょう。\[ a_{n+1}=1+\frac{1}{1+a_n} \]ここで、スタートの $a_1$ は適当な正の数としておきます。 $a_1$ が正の数なら、この漸化式から、すべての自然数 n について $a_n$ も正の数になることは明らかです。また、
\begin{eqnarray}
|a_{n+1}-\sqrt{2}|
&=&
\left| 1+\frac{1}{1+a_n} -\sqrt{2} \right| \\[5pt]
&=&
\left| \frac{1+(1-\sqrt{2})(1+a_n)}{1+a_n} \right| \\[5pt]
&=&
\frac{| 1+1+a_n-\sqrt{2}-\sqrt{2}a_n |}{1+a_n} \\[5pt]
&\lt&
| (1-\sqrt{2})(a_n-\sqrt{2})| \\[5pt]
&=&
(\sqrt{2}-1)|a_n-\sqrt{2}| \\[5pt]
\end{eqnarray}となります(途中に出てくる不等式のところで $a_n$ が正であることを使っています)。
上の結果を繰り返し使えば\[ |a_{n+1}-\sqrt{2}| \lt (\sqrt{2}-1)^n |a_1-\sqrt{2}| \]が得られます。 $n\to\infty$ とすれば右辺は $0$ に収束するため、 $a_n$ は $\sqrt{2}$ に収束することがわかります。つまり、適当な正の数を $a_1$ として\[ a_{n+1}=1+\frac{1}{1+a_n} \]を使って計算していけば、 $\sqrt{2}$ の近似値が得られる、ということです。実際、 $a_1=1$ として計算してみると、
\begin{eqnarray}
a_1 &=& 1 \\
a_2 &=& 1.5 \\
a_3 &=& 1.4 \\
a_4 &=& 1.4166\cdots \\
a_5 &=& 1.4137\cdots \\
a_6 &=& 1.414285\cdots \\
a_7 &=& 1.414201\cdots \\
a_8 &=& 1.414215\cdots \\
a_9 &=& 1.4142131\cdots \\
a_{10} &=& 1.4142136\cdots \\
a_{11} &=& 1.414213552\cdots \\
a_{12} &=& 1.414213564\cdots \\
\end{eqnarray}となり、10回程度計算するだけでだいぶ近い値となります。
ルート2の連分数展開と長方形
上で見た通り、 $\sqrt{2}$ の連分数展開は次のようになります。
\begin{eqnarray}
\sqrt{2}=1+\frac{1}{ \displaystyle 2+\frac{1}{ \displaystyle 2+\frac{1}{ 2+\ddots } }}
\end{eqnarray}これと図形とをリンクさせて考えてみましょう。
次のように、縦が $1$ で横が $\sqrt{2}$ の長方形を考えてみます。日常でよく使うA4やB5といった紙のサイズは、この比率になっています。
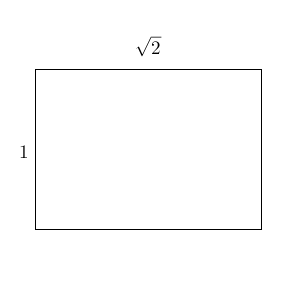
続いて、この長方形を、「正方形と長方形」に分割します。
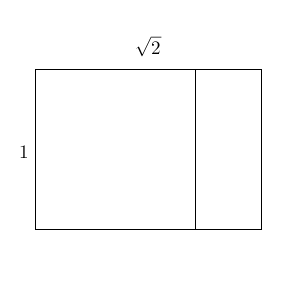
残った長方形(長方形Aと呼びます)を、もう一度「正方形と長方形(長方形Bと呼びます)」に分割します。

右側にできた大きな長方形Aと右下にできた長方形Bは相似になります。そのことを確かめてみましょう。
長方形Aは、短い辺と長い辺の比が $(\sqrt{2}-1):1$ となります。また、右下にできた長方形Bは、長い辺が $\sqrt{2}-1$ で、短い辺が
\begin{eqnarray}
1-2(\sqrt{2}-1)=3-2\sqrt{2}
\end{eqnarray}となります。そのため、短い辺と長い辺の比は
\begin{eqnarray}
(3-2\sqrt{2}):(\sqrt{2}-1)
&=&
\frac{3-2\sqrt{2} }{\sqrt{2}-1}:1 \\[5pt]
&=&
\frac{(3-2\sqrt{2})(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}:1 \\[5pt]
&=&
(3\sqrt{2}+3-4-2\sqrt{2}):1 \\[5pt]
&=&
(\sqrt{2}-1):1 \\[5pt]
\end{eqnarray}となります。長方形Aの比率と同じなので、相似であることがわかります。
これは、長方形を「正方形と長方形」に分割したとき、元の長方形と同じ形の長方形が残る、ということです。これを繰り返せば、この「正方形と長方形を分割する操作」は何度やっても永遠に終わることがない、ということがわかります。
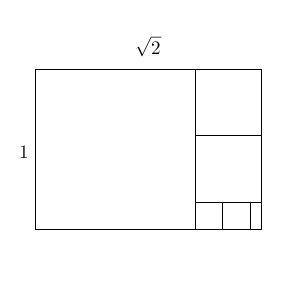
さて、この図形の分割と連分数展開との関連について見ていきましょう。 n 回目の分割で出てくる長方形の短い方の長さを $r_n$ としましょう。一番初めの状態は、\[ \sqrt{2}=1+r_1 \]となります。以後の分割では、長い辺は $r_{n-1}$ であり、一辺が $r_n$ の正方形が2個とれるので、 $(n+1)$ 回目の分割から次の式が得られます($r_0=1$ と考えます)。
\begin{eqnarray}
r_{n-1} &=& 2r_n+r_{n+1} \\[5pt]
\frac{r_{n-1} }{r_n} &=& 2+\frac{r_{n+1} }{r_n} \\[5pt]
\end{eqnarray}これを順番に上に式に入れていくと
\begin{eqnarray}
\sqrt{2}
&=&
1+r_1 \\[5pt]
&=&
1+\frac{1}{\displaystyle \frac{1}{r_1} } \\[5pt]
&=&
1+\frac{1}{\displaystyle 2+\frac{r_2}{r_1} } \\[5pt]
&=&
1+\frac{1}{\displaystyle 2+\frac{1}{\displaystyle \frac{r_1}{r_2} }} \\[10pt]
&=&
1+\frac{1}{\displaystyle 2+\frac{1}{\displaystyle 2+\frac{r_3}{r_2} }} \\[10pt]
\end{eqnarray}これを繰り返していけば、連分数展開の式が出てきます。つまり、「連分数が永遠に終わらない」ということは、「長方形を、『正方形と長方形』に分割していっても、元の長方形と同じ形の長方形が残るので、分割が永遠に終わらない」ということに対応しています。また、連分数展開の分母に出てきた「 $2+$ 」は正方形が2つ取れることと対応しています。
もう一つの有名な例
上では $\sqrt{2}$ の連分数展開を見ましたが、もう一つ有名なものを簡単に見ておきましょう。分母が次のようにすべて $1$ になっているものです。
\begin{eqnarray}
1+\frac{1}{ \displaystyle 1+\frac{1}{ \displaystyle 1+\frac{1}{ 1+\ddots } }}
\end{eqnarray}この値を x とおくと、これが収束するなら、次の式を満たさないといけません(分母の分数と x とをよく見比べてみましょう)。\[ x = 1+\frac{1}{ x } \]これを解くと、
\begin{eqnarray}
x^2-x-1 &=& 0 \\[5pt]
x=\frac{1\pm\sqrt{5} }{2}
\end{eqnarray}となります。この連分数は正の数であることから $\displaystyle x=\frac{1+\sqrt{5} }{2}$ であることがわかります。これは黄金数と呼ばれる数字です。
\begin{eqnarray}
\frac{1+\sqrt{5} }{2} = 1+\frac{1}{ \displaystyle 1+\frac{1}{ \displaystyle 1+\frac{1}{ 1+\ddots } }}
\end{eqnarray}と書けることも、 $\sqrt{2}$ と並んで、よく紹介されます。
おわりに
ここでは、ユークリッドの互除法の関連として連分数を紹介し、有理数の連分数展開と $\sqrt{2}$ の連分数展開について見てきました。 $\sqrt{2}$ の連分数展開は分数が無限に出てきますが、これの図形的な解釈も見ました。近似値を出すのに使うこともできるので、他の分野に応用することもあります。





