【導入】複素数を考える意味について

🕒 2017/06/06 🔄 2023/05/01

実数を2乗すると、必ず0以上になりますよね。2乗して負になることはありません。しかし、複素数の分野では、「2乗して $-1$ になる数」を考えていきます。謎ですね。なぜこんな不思議なものを考えなければいけないのでしょうか。ここでは、複素数を考える意味について、見ていきます。

📘 目次

はじめに

複素数の世界では、2乗して $-1$ になる数、つまり、\[ i^2=-1 \]となる i を導入するところから話が始まります。この i のことを虚数単位といい、2つの実数 a, b を使って\[ a+bi \]と書けるものを複素数といいます。

ただ、いきなりこんなことを言われても、「2乗して $-1$ になる数なんて、存在しないじゃないか。考える意味なんてあるのか」と思いますよね。

ここでは複素数を考える意味として、以下の点について書いていきたいと思います。

回転が扱いやすくなる
つねに方程式の解が存在するようになる
実数の世界で解決できなかった問題が解決できるようになる

複素数を考えることにはメリットもあるし意味もあるのですが、残念なことに、それらはすぐに出てくるわけではありません。これから長い間、数学や自然科学に触れていく人ならメリットを受けられますが、そうでない人にはメリットは少ないかもしれません。そのため、これ以降を読んでも、モヤモヤが解決されない可能性はあります。

それでも、複素数を学ぶその先に、どういった内容が続いていくかを知ることは大事だと思います。

複素数と回転

虚数を考えるメリットの一つに、「回転が扱いやすくなる」というものがあります。これについて、まずは見ていきましょう。

$3$ に $-1$ を掛けると、 $-3$ になります。また、 $-3$ に $-1$ を掛けると、 $3$ になりますよね。

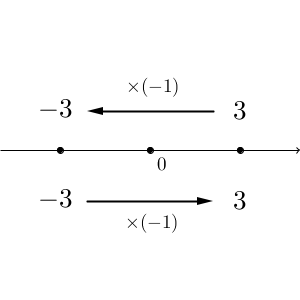
このことを数直線上で考えれば、「$-1$ を掛けると、（原点を中心に）反対側へ移動する」と見ることができます。また、少し見方を変えれば、「（原点を中心に）180度回転した」と見ることもできますよね。

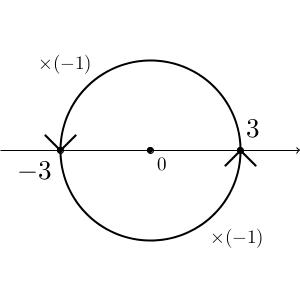
180度の回転があるのだったら、その間の回転もあっていいはずです。「2乗して $-1$ になる数 $=i$ 」というのは、「その数を掛けることが、90度の回転に対応するもの」と考えることができます。

「2乗して $-1$ になる数」というよりも「90度の回転」と言われたほうが、少しは「考える意味がありそう」という気になってきませんか？　両者は同じ内容を指しているのに、言い換えただけで印象が変わりますね。

しかも、この「回転」の考えは、90度以外にも応用することができます。実数と虚数単位 i を組み合わせれば、45度の回転や30度・60度の回転、一般の角度の回転も表現することができます。例えば、45度の回転というのは、\[ \cos 45^{\circ} + i \sin 45^{\circ} \]を掛けることに対応します。

回転した後の座標というのは、一般的に扱いにくいものなんですが、複素数を導入すると「回転」を「複素数の掛け算」で表現できるため、扱いやすくなるんですね。

先ほどから「回転」と言っていますが、回転していなくても応用できます。例えば、正三角形ABCがあったとすると、「点Aは、点Bを中心に点Cを60度回転したもの」と考えることで、2つの点の座標と複素数の掛け算を組み合わせて、もう1つの点の座標を簡単に表すことができるようになります。

しかも、「複素数の足し算」は平行移動に対応するため、図形の問題を「複素数の計算の世界」で考えられるようになります。

複素数の内容を図形の問題に応用することができるんですね。こうした内容は、複素数平面の分野で学ぶのですが、これを学ぶのは少し先です。文系の範囲には入っていないので、複素数の便利さを学ぶ前に終わってしまいます。そのため、文系の人にとっては存在意義が謎のまま終わってしまうかもしれません。

複素数と方程式

上では、複素数と回転について書きましたが、数学的な意味で言えば、複素数は方程式を考える上で重要な意味を持っています。ここでは、その点について書いていきます。

小学校時代の算数から、数の範囲はだんだん広がってきましたね。はじめは自然数だけでした。自然数の世界では、足し算と掛け算が自由にできますが、割り算ができるとは限りません。しかし、分数も加えれば、割り算も自由にできるようになります。

中学生になって負の数を学んだ結果、引き算も自由にできるようになりました。これで、四則演算が自由にできます。これは、方程式の世界では\[ ax+b=0 \]という一次方程式の解をいつでも求められるようになった、ということができます。 a, b が有理数の世界では、($a\ne 0$ なら)この方程式はつねに解けて、\[ x=-\frac{b}{a} \]となり、有理数の世界で答えを求めることができます。

しかし、二次方程式になると、有理数の世界では解けるとはかぎりません。\[ x^2=2 \]の解は $x=\pm\sqrt{2}$ であり、これは有理数の形では書けません。そこで、無理数を導入し、数の世界は実数へと広がりました。

こうして考えると、方程式が解けるように、今まで数の概念をどんどん拡大してきたんですね。ただ、実数の世界に拡大しても、すべての二次方程式に解があるとは限りません。\[ x^2=-1 \]となる実数はないからです。まだ足りません。

ここで、数学の世界では、「数の世界を、より広げよう」と考えます。今までも、「小さい数から大きい数は引けないから、考えるのはやめよう」「奇数を2で割ることができないから、考えるのはやめよう」「2乗して2になる数はないから、考えるのはやめよう」とはなりませんでした。今まで数の世界を広げるたびに、いろいろな問題が解けるようになったため、今回も同じように広げてみるんですね。

複素数まで数の世界を広げた結果、数学の世界ではとても重要なことにたどり着きました。それは、「代数学の基本定理」という名前のついた、次のような内容です。

代数学の基本定理

複素数を係数に持つ n 次の方程式は、重複を含めて n 個の複素数解を持つ。

これは、「複素数まで数を広げれば、その世界で考える方程式には、すべての解がその世界にある」ということを意味しています。なお、「重複を含めて」というのは、例えば $(x-1)^2=0$ というような重解は、2個と数える、ということです。

この「代数学の基本定理」にたどり着いたことにより、今まで方程式が解けるように数の世界を広げてきたけれども、「（方程式を解くという観点で）数の世界を広げていくことは終わった」と考えることもできるわけですね。

そういう意味で、数学の世界では、「複素数」は重要な意味を持っています。

ただ、高校の範囲で、この「代数学の基本定理」を証明するのは難しいです。それに、これを使って何か問題を解くというケースも少ないです（重要な定理なので、教科書で紹介されていることは多いですが）。なので、ここでも、導入するメリットをすぐには得られません。

複素数の世界で実数の問題を解く

数学のいくつかの問題では、「見た目は実数の問題なのに、なぜか答えに複素数が出てくる」ということがあります。例えば、\[ 1,1,0,-1,-1,0,1,1,\cdots \]というように、 $1,1,0,-1,-1,0$ がずっと続いていく数字の列があったとします。この n 番目の数を n を使って表そうとすると、\[ \frac{1}{\sqrt{3} i} \left\{\left(\frac{1+i\sqrt{3} }{2}\right)^n - \left(\frac{1-i\sqrt{3} }{2}\right)^n\right\} \]という式になります。なぜか複素数が出てきます。

また、「見た目は実数の問題なのに、なぜか複素数の世界で考えると解ける」ということもあります。（まだ習っていない人も多いでしょうが、）実数の世界である積分を計算するときに、複素数の世界で考えると簡単に計算できる、ということがあります。よく挙がる例としては、\[ \int_{-\infty}^{\infty} \exp (-x^2)dx = \sqrt{\pi} \]というものがあります。この式はすべて実数の世界の話なのですが、なぜか複素数の世界に寄り道すると計算しやすくなる、という不思議なことが起こります。

このように、複素数は、表面上実数しか出てこない場合でも登場することがあります。実数の世界の中にも、こうした複素数が絡んでくるというのは、とても不思議な感じがしますね。