【応用】二次関数の最小値の最大

ここでは、「二次関数の最小値が最大になるとき」というような問題を考えていきます。問題文を読んで意味が分からない場合は、【応用】「最小値の最大」問題は何をやっているかを先に読むといいと思います。

例題

これを解くには、まず「関数 $y=x^2-2ax+2a+1 \ (0\leqq x \leqq 2)$ の最小値」を考えます。これは、【応用】二次関数の最大・最小（軸が動く）の例題(1)で見た内容と同じです。

最小値を求めるところまで簡単に振り返ると、まずは、頂点を求めるんでしたね。
\begin{eqnarray} y &=& x^2-2ax+2a+1 \\ &=& (x-a)^2-a^2+2a+1 \\ \end{eqnarray}これから、頂点が $(a,-a^2+2a+1)$ だとわかるので、今考えている定義域とこの頂点との位置関係から考えて、最小値を求めます。区間の左端・頂点・区間の右端で最小となるときで場合分けをして、最小値は次のようになります（ここでは省略していますが、実際の答案では場合毎にグラフの概形をかきましょう）。

　$a \lt 0$ のときの最小値は $2a+1\ (x=0)$
　$0\leqq a \leqq 2$ のときの最小値は $-a^2+2a+1\ (x=a)$
　$2\lt a$ のときの最小値は $-2a+5\ (x=2)$

このように a の値によって、最小値の表し方が変わってくるんですね。ここまでは $x, y$ の関係を見てきましたが、ここからは $a, m$ の関係に頭を切り替えて考えていきます。上のことから $a, m$ の関係を書けば、次のようになります。

　$a \lt 0$ のときは $m=2a+1$
　$0\leqq a \leqq 2$ のときは $m=-a^2+2a+1$
　$2\lt a$ のときは $m=-2a+5$

問題は、これの最大値を求めることです。最大を求めるために、このグラフをかきます。ここで考えるグラフは、 a と m との関係を表すグラフです。

$0\leqq a \leqq 2$ のときの式を平方完成すると
\begin{eqnarray} m &=& -a^2+2a+1 \\ &=& -(a-1)^2+2 \\ \end{eqnarray}となります。普段と変数が違うので変な感じがしますが、やることは同じです。

これらのことを踏まえてグラフをかくと、次のようになります。

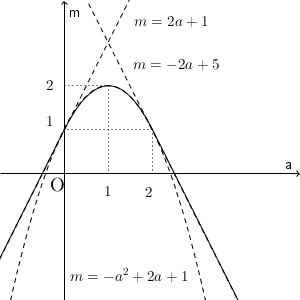
線がたくさんあって少しわかりづらいですが、 $a \lt 0$ と $2\lt a$ の範囲は直線の一部、その間は放物線の一部となっています。グラフを見ると、 $m$ が最大になるのは $a=1$ のときで、その値は $m=2$ であることがわかります。これが答えとなります。つまり、

　$a=1$ のときに m は最大値 $2$ をとる

が答えです。

おわりに

ここでは、「二次関数の最小値が最大になるとき」を見ましたが、他にもバリエーションはあります。「最大値が最小になるとき」「最小値が最小になるとき」「最大値が最大になるとき」という問題も作ることができます。

ただ、どういうときでもやることは同じで、まずは最小値や最大値がどうなるかを求めます（この段階では $x,y$ のみを動かしている）。次に、他の文字を動かします。上の問題で a を動かして m を変化させる、という要領ですね。これで求めたいものが得られます。

文字がたくさん出てきてわかりづらいですが、何を固定して何を動かしているか、を意識して解くようにしましょう。