【応用】二次関数の最大・最小（変数置き換え）

ここでは、「見た目は四次関数だけど、変数置き換えによって二次関数に帰着できる」場合での、最大値・最小値を考えます。

例

例えば、 $y=x^4+2x^2+1$ という関数の最小値を考えてみましょう。見た目は四次関数ですが、 $t=x^2$ とすれば、次のように二次関数になります。
\begin{eqnarray} y &=& t^2+2t+1 \\ &=& (t+1)^2 \\ \end{eqnarray}これからグラフをかけば次のようになる、ような気がします。

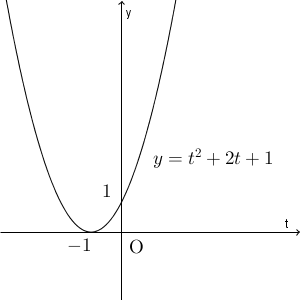
これから最小値は $y=0$ となるような気がするのですが、実際にはそうはなりません。というのも、 $y=0$ になるには、 $t=-1$ でないといけません。 $t=x^2$ だったので、 $x^2=-1$ とならないといけませんが、こんなことは起こりません。なので、 $y=0$ となることはなく、これが最小値とはいえません。

【応用】二変数二次関数の最大・最小（隠れた条件付）のところでやったように、変数を消去する場合は、条件に気をつける必要があります。今の場合、 $t=x^2$ とおいた時点で $t\geqq 0$ という条件を考慮しないといけないんですね。つまり、正しいグラフは次のようになります。

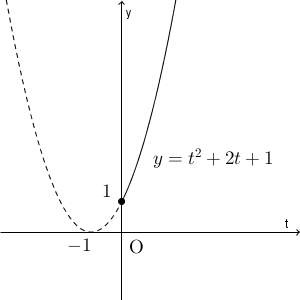
これから、 $t=0$ 、つまり、 $x=0$ のときに最小値 $y=1$ となることがわかります。

このことを踏まえて次の例題を考えてみましょう。

例題

式を見れば、これを展開するのではなくて $t=x^2-2x+2$ などとして文字を置き換えるのだろう、ということに気づくと思います。つまり、 $y=-t^2-4t+5$ を考えればいいということですね。

ここで注意しないといけないのは、t がどんな値をとり得るか、ということです。これによって、置き換えた後の二次関数の定義域が変わってきます。まずは、t のとり得る範囲を考えます。

\begin{eqnarray} t &=& x^2-2x+2 \\ &=& (x-1)^2+1 \\ \end{eqnarray}となるので、グラフは次のようになります。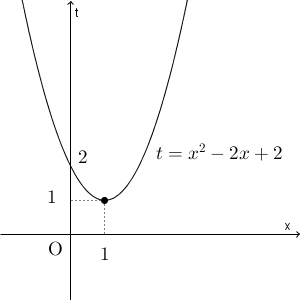

このグラフから、t のとり得る範囲は $t\geqq 1$ となることが分かります。次に y を変形すると次のようになります。

\begin{eqnarray} y &=& -t^2-4t+5 \\ &=& -(t^2+4t)+5 \\ &=& -(t+2)^2+9 \\ \end{eqnarray}このことと $t\geqq 1$ から、グラフは次のようになります。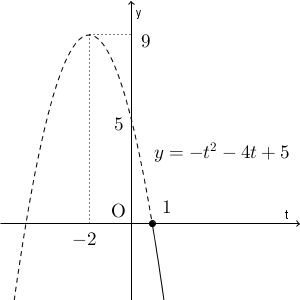

よって、 $t=1$ のとき、つまり、 $x=1$ のときに最大値 $y=0$ をとることがわかります。これが答えです。

おわりに

自分で新しい変数を使って文字を消去する場合も、「その変数に条件がつくかどうか」を考えなくてはいけません。すべての値をとり得るか（上の例であれば、「t がすべての実数値をとりうるかどうか」）に注意して問題を解くようにしましょう。