【応用】二次関数の最大・最小（区間が動く）

【標準】二次関数の最大・最小（区間が広がる）では、定義域の区間が広がったり狭くなったりしたときに、二次関数の最大値・最小値がどうなるかを見ました。ここでは、区間が動く場合を考えてみます。イメージするのがだんだん難しくなってきます。

例題1

頂点を求めると次のようになります。
\begin{eqnarray} y &=& -x^2+8x-6 \\ &=& -(x-4)^2+16-6 \\ &=& -(x-4)^2+10 \\ \end{eqnarray}これから、頂点が $(4,10)$ であることがわかります。

今考える範囲は $a\leqq x \leqq a+2$ なので、区間の幅は一定ですが、区間が左右に動くんですね。 a の値によって区間がどう変わるかを示したものが次のグラフになります。

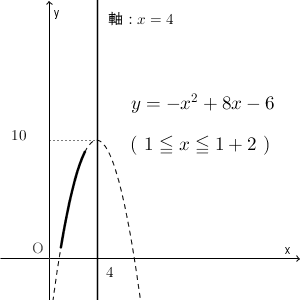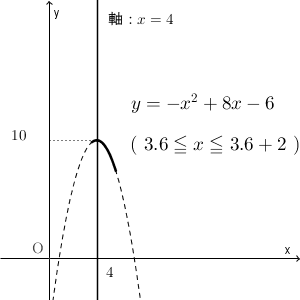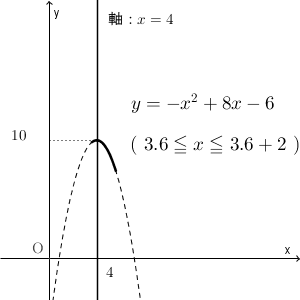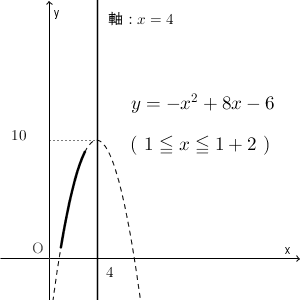
これを見ながら、 a が大きくなるにつれて、最大値をとる場所がどう変わるか考えてみましょう。よく見ていると、 a が小さいうちは区間の右端で最大となり、途中からは頂点で最大となり、やがて区間の左端で最大となる、というように変化していくことがわかります。

この状況の境目はどこでしょうか。まず、「区間の右端で最大」となる状況から「頂点で最大」となる状況へ切り替わるタイミングは、区間の中に頂点が含まれるタイミングであることがわかります。つまり、区間の右端が頂点と重なる $a+2=4$ のタイミング（ $a=2$ のとき）で切り替わるんですね。区間がこのときより左にあれば「区間の右端で最大」、右にあれば「頂点で最大」となります。

次に、「頂点で最大」から「区間の左端で最大」に切り替わるタイミングを考えます。これは、区間から頂点がはずれるタイミングであることがわかります。つまり、区間の左端が頂点と重なる $a=4$ のときですね。区間がこれより左なら「頂点で最大」、右にあれば「区間の左端で最大」となります。

また、頂点、区間の左端での x 座標はそれぞれ $4$, $a$ なので、y 座標はそれぞれ $10$ 、 $-a^2+8a-6$ であることがわかります。区間の右端の y 座標は、 $x=a+2$ を代入して
\begin{eqnarray} & & -(a+2)^2+8(a+2)-6 \\ &=& -a^2-4a-4+8a+16-6 \\ &=& -a^2+4a+6 \\ \end{eqnarray}と求められます。

以上から、答えは次のようになります。

　$1\leqq a \lt 2$ のときの最大値は $-a^2+4a+6\ (x=a+2)$
　$2\leqq a \leqq 4$ のときの最大値は $10\ (x=4)$
　$4\lt a \leqq 5$ のときの最大値は $-a^2+8a-6\ (x=a)$

最大値をとる場所が a の値によって異なるので、このように場合分けをして答えることになります。

例題2

続いて、(2)を考えます。

区間によって最小値をとる場所がかわることは、同じグラフを見ればわかると思います。

はじめのうちは左端、やがて右端で最小値をとることになります。この状況の境目は次の場面です。

区間の両端が同じ高さになったときです。放物線は軸に関して左右対称で、区間の幅が $2$ なので、区間の両端が同じ高さになるのは $a+1=4$ のとき（区間の中心が放物線の軸上に来るとき）であり、このとき区間の両端で最小値をとります。その最小値は $x=3$ を代入して $y=9$ と求められます。また、これより左の区間なら区間の左端で、右なら区間の右端で最小値をとることが分かります。

以上から、答えは次のようになります。

　$1\leqq a \lt 3$ のときの最小値は $-a^2+8a-6\ (x=a)$
　$a=3$ のときの最小値は $9\ (x=3,5)$
　$3\lt a \leqq 5$ のときの最小値は $-a^2+4a+6\ (x=a+2)$

$a=3$ のときは、区間の両端で最小値をとるので、別格扱いをします。上の3つをまとめたものが答えです。

おわりに

上では区間が動くグラフを見ながら考えましたが、実際の試験などでは頭の中でイメージする必要があります。区間が動いたときにどこで最大値・最小値をとるか、を考えて、場合分けをして答えるようにしましょう。