【応用】二次関数の最大・最小（応用問題）

ここでは、二次関数の最大値・最小値を求める問題の応用例を見ていきます。問題文を読んで二次関数を作り、その最大値や最小値を求めます。定義域の範囲に注意しながら考えていきましょう。

例題

まずは、商品の値段と売り上げの関係を式にしてみましょう。

$10x$ 円値上げするとすると、値段は $100+10x$ となり、売上数は $100-5x$ となります。なので、売り上げは次のようになります。
\begin{eqnarray} & & (100+10x)(100-5x) \\ &=& -50x^2+500x+10000 \\ &=& -50(x^2-10x)+10000 \\ &=& -50(x-5)^2+1250+10000 \\ &=& -50(x-5)^2+11250 \\ \end{eqnarray}次にグラフをかくのですが、その前に定義域を考えます。商品の値段、売り上げ数がマイナスになることはないので、 $-10\leqq x \leqq 20$ となることがわかりますね。これを踏まえてグラフを描くと次のようになります。

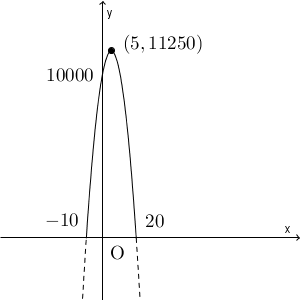
これから、 $x=5$ 、つまり、 $5x=50$円値上げをすればいい、ということがわかります。これは問題に適している（値段が負の数になったり小数になったりしていない）ので、これが答えになります。

おわりに

自分で二次関数を作って最大・最小を考える問題は、次のようなステップに分かれます。

• わからないものを文字で置いて、二次関数を作る
• 定義域の範囲を考える
• グラフをかいて、関数の最大・最小を求める
• 得られた答えが問題に適しているかチェックする

一つ目のステップは、二次関数の問題というよりは、「問題文を読んで式を作る問題」です。式を作る能力がないと、そもそもその後のステップがまったくできないので、応用問題もしっかり練習しましょう。