【応用】二変数二次関数の最大・最小（隠れた条件付）

【応用】二変数二次関数の最大・最小（条件付）では、条件のついている2つの変数が入った二次関数の最大値・最小値を求める問題を見ました。ここでは、同じような問題を考えるのですが、隠れた条件がついているものを取り上げます。

途中で、二次不等式の話が出てくるので、そこを勉強してからの方が分かりやすいと思います（参考：【導入】二次不等式）。

例題

次の例題を考えてみましょう。

【応用】二変数二次関数の最大・最小（条件付）では、変数に範囲が指定されていましたが、今回は特に指定されていません。式を見ると、条件式を使って $y^2$ を消す方針で考えたほうがよさそうですね。

条件式から $y^2=1-x^2$ なので、 $z=2x+y^2$ とおくと、次のように変形できます。
\begin{eqnarray} z &=& 2x+y^2 \\ &=& 2x+(1-x^2) \\ &=& -x^2+2x+1 \\ &=& -(x^2-2x)+1 \\ &=& -(x-1)^2+2 \\ \end{eqnarray}これから、グラフは上に凸のグラフになることが分かります。しかし、どこまでも小さな値をとることができるか、というとそうではないんですね。例えば、 $x=100$ とすると、上の式の z は小さな値になりますが、 $x^2+y^2=1$ を満たす実数 y が存在しません。二乗してマイナスになる実数はありませんからね。

つまり、 x はどんな数でもいいわけではない、ということです。見えないけれど、条件があったんですね。それは、 $y^2\geqq 0$ という条件です。【応用】二変数二次関数の最大・最小（条件付）で、「文字を消去するときには、その文字に関する条件も考慮しないといけない」と書きましたが、ここでも同じです。実数なら二乗して0以上になるという条件を考慮しないといけません。書いていないけど、自分で思いつかなくてはいけいけません。

さて、文字を消去するために $y^2=1-x^2$ という条件式を使いましたが、 y は実数なので x には $1-x^2\geqq 0$ という条件があることに注意しないといけないんですね。二乗して1以下なので、 $-1 \leqq x \leqq 1$ という条件になります（ここの変形は、厳密には二次不等式の部分で学びます）。この範囲で考えないといけません。

以上から、グラフは次のようになります。

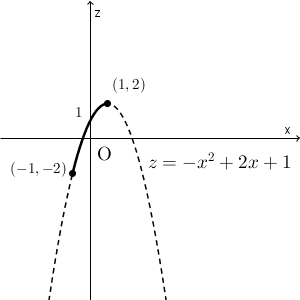
このことから、 $x=1, y=0$ のとき最大値 $2$ をとり、 $x=-1,y=0$ のとき最小値 $-2$ をとることがわかります。

おわりに

$x,y$ がとり得る値の範囲が書かれていないのに、自分で気づかないといけない点が難しいです。「実数」と書かれた変数を消去するときに、「そのような実数はきちんと存在するか」を意識するようにしましょう。特に、二乗されている場合（上の例題のようなケース）で「負にならない」という条件を使う場面はよくあるので覚えておきましょう。