【基本】対偶証明法

🕒 2016/07/02 🔄 2023/05/01

ここでは、命題の対偶を使った証明方法について見ていきます。対偶については、【基本】逆・裏・対偶でも出てきたので、忘れてしまった人はチェックしておきましょう。

📘 目次

対偶証明法

命題を考えるときに、条件を満たす集合を使うと考えやすくなる、ということを【基本】命題と集合で見ました。ここでも、この考え方を使ってみます。

命題 $p\implies q$ に対し、条件 p, q を満たすものの集合をそれぞれ P, Q とします。このとき、 $p\implies q$ が成り立つことと $P\subset Q$ が同じ意味になるんでしたね（参考：【基本】命題と集合）。

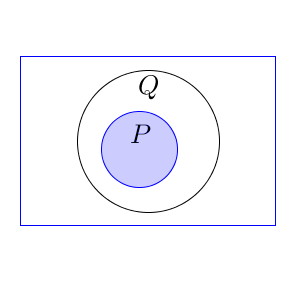
次に、 $p\implies q$ の対偶を考えてみます。対偶は、 $\bar{q}\implies \bar{p}$ となります。それぞれのパーツを集合で考えると $\overline{ Q }$ と $\overline{ P }$ に対応します。P が Q に含まれるのだから、上の図からもわかる通り、Q 以外の部分はP 以外に含まれます。よって、 $\overline{ Q } \subset \overline{ P }$ となります。

以上のことをまとめると、 $p\implies q$ が成り立つ時、 $\bar{q}\implies \bar{p}$ が成り立つことが分かります。

また、同様に考えれば、 $\overline{ Q } \subset \overline{ P }$ ならば、 $P\subset Q$ が成り立つこともわかるので、 $\bar{q}\implies \bar{p}$ が成り立つ時、 $p\implies q$ が成り立つことが分かります。

これらのことから、次のことが分かります。

対偶の真偽

命題 $p\implies q$ と、この対偶 $\bar{q}\implies \bar{p}$ の真偽は一致する

このことから、「 $p\implies q$ が成り立つことを示しなさい」と言われれば、対偶を証明してもいいことが分かります。具体的に、証明問題でどのように使うかは、例を使って見てみましょう。

例題

次の命題を証明せよ。
　nを整数とするとき、 $n^2$ が4の倍数でないならば、 $n$ は4の倍数でない

「 $n^2$ が4の倍数でない」というのが扱いにくそうです。一方、結論を否定したものは「 $n$ は4の倍数である」となり、扱いやすそうです。こういう場合は、もとの命題を証明するよりも、対偶を証明したほうが楽になります。

証明

もとの命題の対偶は次のようになる。
　「nを整数とするとき、 $n$ が4の倍数ならば、 $n^2$ は4の倍数である」
$n$ が4の倍数のとき、ある整数 m を使って $n=4m$ と書ける。このとき \[ n^2 =16m^2 =4\times 4m^2\]なので、 $n^2$ は4の倍数となる。
よって、対偶が真なので、もとの命題も真となる。
（証明終）

もとの命題とその対偶の真偽は一致するので、命題を直接示しにくいときは対偶を示すことができないか、考えたほうがいいんですね。

ここで挙げた例は、【基本】逆・裏・対偶でも使った例です。上の命題を直接示す方法もリンク先のページで書いていますが、直接示すのは少し難しいことが分かります。