【基本】直線の極方程式

ここでは、直線の極方程式を見ていきます。

直線の極方程式その１

ここでは、直線の極方程式を見ていきますが、まずはすごくシンプルな場合を考えます。極 $\mathrm{O}$ を通るものを考えます。

極 $\mathrm{O}$ を通り、始線とのなす角が $\alpha$ である直線 $\ell$ を考えます。角は反時計回りを正の方向とします。このとき、 $r,\theta$ はどのような方程式で表されるでしょうか。

まずは、始線を $\alpha$ だけ回転した半直線を考えます。

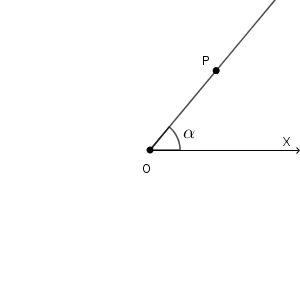
この半直線上にある点 $\mathrm{P}(r,\theta)$ をとります。 $\theta$ は $\alpha$ と一致していないといけません。また、 $r$ は正の値ならなんでもよく、 $\mathrm{P}$ を動かせば、正の値をすべてとりえることがわかります。なので、\[ \theta=\alpha,\ r\gt 0 \]を満たす点をすべて集めると、回転後の半直線（極は除く）と一致することがわかります。

$\theta=\alpha$ を満たしたまま、 $r$ を動かしてみます。 $r=0$ のときは極を表します。 $r\lt 0$ の場合は、 $(-r,\theta+\pi)$ を考えればいいのでした（参考：【基本】極座標）。つまり、始線を $\alpha+\pi$ だけ回転した半直線を表すことになります。

以上から、\[ \theta=\alpha \]を満たす点をすべて集めれば、直線 $\ell$ と一致することがわかります。そのため、これが、直線 $\ell$ の極方程式となります。

シンプルですね。

直線の極方程式その２

今度は、極を通らない場合を考えます。その中でも式がシンプルである、始線に垂直な直線を考えます。

点 $\mathrm{A}(a,0)$ を通り、始線に垂直な直線 $\ell$ の極方程式を考えます。

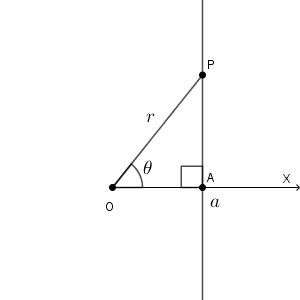
$\mathrm{P}$ が始線上にない場合は、三角形 $\mathrm{OAP}$ が直角三角形になります。なので、\[ r\cos\theta=a \]という関係式が成り立ちます。なお、この関係式は、 $\mathrm{P}$ が始線上にある場合も成り立ちますし、 $a$ が負であっても成り立ちます。

逆に、 $r\cos\theta=a$ を満たしていれば、点 $\mathrm{P}$ は、 $\mathrm{A}$ を通り、 $\mathrm{OA}$ に垂直な直線上にあります。

こうして、 $r\cos\theta=a$ を満たす点全体は、直線 $\ell$ と一致することがわかります。

円の極方程式と直線の方程式は形が似ていて、見た目が紛らわしいです（参考：【基本】円の極方程式）。\[ r=a\cos\theta \]は極と $(a,0)$ を直径の両端とする円の極方程式であり、\[ r\cos\theta=a \]は $(a,0)$ を通り、始線に垂直な極方程式です。直角三角形をイメージしながら図をかくとわかりやすいでしょう。

直線の極方程式その３

最後に、一般的な場合を考えます。

点 $\mathrm{A}(a,\alpha)$ を通り、 $\mathrm{OA}$ に垂直は直線 $\ell$ の極方程式を考えます。この直線上の点 $\mathrm{P}$ を考えます。

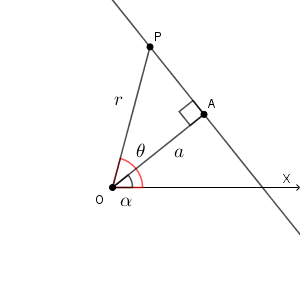
先ほどと同じように、直角三角形 $\mathrm{OAP}$ を使うのがよさそうです。線分 $\mathrm{OA}$ の長さは $a$ で一定です。なので、 $r$ を使うと、\[ r\cos\angle\mathrm{AOP}=a \]という関係式が成り立ちます。角は $\theta, \alpha$ を使って表せるので、結局、\[ r\cos(\theta-\alpha)=a \]となります。

逆に、 $r\cos(\theta-\alpha)=a$ を満たしていれば、点 $\mathrm{P}$ は、 $\mathrm{A}$ を通り、 $\mathrm{OA}$ に垂直な直線上にあります。

始線に垂直な場合は $\alpha=0$ とした式に対応しています。

おわりに

ここでは、直線の極方程式を見ました。極を通る場合や、始線に垂直な場合、そして、一般の場合を見ました。