🏠 Home / 数学C / 平面上の曲線 / 極座標

【基本】円の極方程式

🕒 2022/12/03 🔄 2023/05/03

ここでは、極方程式を見ていきます。最もシンプルな円の極方程式を見ます。

📘 目次

極方程式

直交座標の世界では、円の方程式は\[ x^2+y^2=a^2 \]となるのでした。この方程式を満たす点をすべて集めると、原点を中心とした半径 $a$ の円となります。

極座標の世界でも、 $r,\theta$ を使って、曲線を表すことができます。ある曲線が、 $r,\theta$ に関する方程式で表されるとき、その方程式を曲線の 極方程式(polar equation) といいます。

以下では、具体的な極方程式を見ていきます。

円の極方程式その１

極方程式の例として、中心が極で、半径が $a$ の円について考えましょう（ $a\gt 0$ とします）。

この円上の点 $\mathrm{P}$ の極座標を $(r,\theta)$ とします。 $r,\theta$ はどのような方程式で表されるでしょうか。

まず、極からの距離 $r$ は、半径と同じ $a$ でないといけません。一方、角度 $\theta$ はどんな値もとり得ます。逆に、 $r=a$ を満たせば、 $\theta$ がどんな値でも、その点はこの円の円周上にあります。

ということで、この円の極方程式は\[ r=a \]となります。

円の極方程式（円の中心が極の場合）

極を中心とする半径 $a$ の円の極方程式は\[ r=a \]

シンプルですね。

円の極方程式その２

今度は、中心が極ではなく、始線上にある場合を考えます。

中心が $\mathrm{A}(a,0)$ で、半径が $a$ の円があるとします。この円の極方程式を求めましょう。

中心と極との距離が $a$ で、半径も $a$ なので、この円は極を通ります。そのため、 $\mathrm{B}(2a,0)$ とすると、円周上の点 $\mathrm{P}$ が始線上にない場合は、 $\triangle \mathrm{OPB}$ は直角三角形となります。

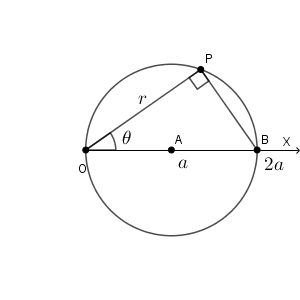
なので、\[ 2a\cos\theta=r \]の関係式が成り立ちます。

逆に、 $r,\theta$ が\[ 2a\cos\theta=r \]を満たしているとします。このとき、 $\angle \mathrm{OPB}=90^{\circ}$ とわかるので、円周角の定理の逆から、点 $\mathrm{P}$ は $\mathrm{OB}$ を直径とする円周上の点だとわかります。

また、 $(r,\theta)=(0,90^{\circ})$ や $(r,\theta)=(2a,0^{\circ})$ は、 $r=2a\cos\theta$ を満たすことから、極 $\mathrm{O}$ や $\mathrm{B}$ もこの方程式の表す曲線上にあることがわかります。

こうして、 $r=2a\cos\theta$ を満たす点全体は、点 $\mathrm{A}$ を中心とした半径 $a$ の円の円周だとわかります。

円の極方程式（円の中心が始線上にある場合）

点 $(a,0)$ を中心とする半径 $a$ の円の極方程式は\[ r=2a\cos\theta \]

$2$ が邪魔なので、次のようにいう場合もあります。

「極と点 $(a,0)$ が直径の両端となるような円の極方程式は $r=a\cos\theta$ 」

方程式を見てもどんな図形かは少しわかりにくいです。直交座標のときよりもピンときにくいですが、図をかけば円を表していることがわかるでしょう。