【基本】条件「かつ」「または」の否定

条件の否定については、【基本】条件の否定で見ましたが、ここでは、条件に「かつ」や「または」を含んだ場合の否定を考えます。間違いやすい項目です。

「かつ」「または」と集合

【基本】命題と集合では、「条件」と「その条件を満たす集合」の対応を見ました。「命題が真であるか偽であるか」と、「条件に対応する集合に包含関係があるかないか」が対応しているんでしたね。

この条件に「かつ」や「または」が含まれていた場合、集合とはどう対応するのか考えてみましょう。条件 p, q とこれらに対応する集合を P, Q とします。このとき、「p かつ q」というのは、両方の条件を満たすものなので、対応する集合で考えると $P\cap Q$ になることがわかります。例えば「x は偶数かつ素数」という条件なら、偶数の集合と素数の集合の交わっている部分、つまり $\{2\}$ という集合が対応する、ということですね。

一方、「p または q」という条件は、少なくとも片方の条件を満たすということなので、対応する集合で考えると $P\cup Q$ になります。

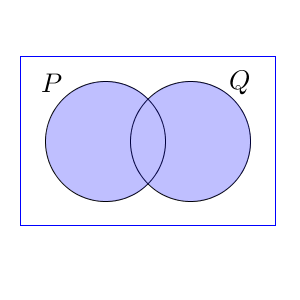
まとめると、条件の「かつ」は集合で言えば「共通部分」にあたり、「または」は「和集合」にあたる、ということです。

ド・モルガンの法則

【標準】ド・モルガンの法則（集合）で見たように、共通部分や和集合の補集合は次のようになるのでした。

「"TDLにもUSJにも行ったことがある人"以外」の集合が、「TDLに行ったことがない、または、USJに行ったことがない人」の集合になるんでしたね。

集合と条件の対応を考え、この集合版の「ド・モルガンの法則」を、「条件」に関する言葉で書き直せば、次のようになります。

少し話が抽象的なまま進んでしまいました。【標準】ド・モルガンの法則（集合）には、もう少しわかりやすい例で説明しているので、わかりにくいと感じた人はそちらも見てみましょう。

条件「かつ」「または」の否定の例

ここでは、「かつ」や「または」を含んだ条件の否定を、具体的な例で考えてみましょう。

「ド・モルガンの法則」を機械的に適用すると、「条件の否定」は、それぞれの条件を否定に変えて、「かつ」と「または」も入れ替えることになります。

(1)であれば、 $x=0$ の否定が $x\ne 0$ 、$y=0$ の否定が $y\ne 0$ 、そして、「かつ」を「または」に変えます。(1)の否定は、次のようになります。

「 $x\ne 0$ または $y\ne 0$ 」

「かつ」を「または」に置き換えることを忘れないようにしましょう。

(2)も同様に考えると、「 $x\gt 1$ かつ $x\lt 2$ 」となります。イコールをとることを忘れてはいけません。なお、この式は1つにまとめることができるので、「 $1\lt x \lt 2$ 」が答えになります。これは、【基本】条件の否定 #条件の否定の例の最後の例に対応しています。否定の否定が元に戻っていることも分かります。

(3)は「かつ」も「または」も出てきていませんが、「a は偶数 かつ b は偶数」と同じことです。なので、この否定は「a は奇数 または b は奇数」となります。また、このことを「a, b の少なくとも一方は奇数」とまとめることもあります。

「ともに」の否定が「少なくとも一方」になるというのも、よく使います。逆に、「少なくとも一方」の否定が「ともに」になるのも、よく使います。数学の問題というよりは、国語の問題に近いですね。

(4)の「 $a=b=0$ 」にも、「かつ」や「または」が出てきていません。しかし、これは「 $a=0$ かつ $b=0$ 」のことです。なので、この否定は「 $a\ne 0$ または $b\ne 0$ 」となります。

おわりに

ここでは、「かつ」や「または」を含んだ条件の否定を見てきました。集合との対応を考えれば、集合のときに考えたことがそのまま応用できます。「かつ」の否定が「または」、「または」の否定が「かつ」になることをおさえておきましょう。ここは間違いやすいポイントです。