【基本】中間値の定理
ここでは、中間値の定理について見ていきます。少し変わった存在型の定理です。
中間値の定理
【基本】連続関数で見たように、定義域のすべての $x$ の値で連続であるとき、その関数は連続関数というのでした。また、閉区間で連続な関数は、その区間内で最大値・最小値を持つことも見ました。
ここでは、閉区間で連続な関数について、他の性質を見ていきます。
関数 $f(x)$ が、閉区間 $[a,b]$ で連続であるとします。つまり、 $a\leqq x\leqq b$ のどの値でも連続、ということですね。このとき、グラフは次のようになります。

グラフの形はわかりませんが、 $a\leqq x\leqq b$ の区間では、グラフは1本の線でつながっています。また、両端も含まれています。
この図からわかることは、 $f(a)\ne f(b)$ のとき、 $f(x)$ は $f(a)$ と $f(b)$ の間のすべての値を、少なくとも1回はとる、ということです。それは、 $y=f(a)$ と $y=f(b)$ の間に、 $x$ 軸に平行な線(上の図の点線)をひくと、グラフと少なくとも1点で交わっていることからわかります。
これは、上のグラフがたまたまそうなっているわけではなく、閉区間で連続であれば、成り立ちます。いろいろグラフをかいて確かめてみましょう。
本来は、証明が必要な内容ですが、高校数学の範囲では示すことはできません。そのため、学校の教科書にも証明は書いていませんが、試験や入試では使っていい内容です。このことは、「間の値をとる」ということから、中間値の定理(intermediate value theorem) と呼ばれています。
また、この内容を使えば、 $f(a)$, $f(b)$ が異符号なら、 $f(x)=0$ を満たす実数解が $a\lt x\lt b$ 内に少なくとも1つあることがわかります。これも、応用バージョンとして、よく使われます。
これらは数学の定理の中でも少し変わった内容です。「存在する」ことは言っていますが、どんな値か、どこに存在するかまでは言っていません。
例えば、「宇宙人はどこにいるかはわからないけど、存在することはわかる」と言っても、普通なら相手にされないでしょう。しかし、数学の場合は、「解が何かはわからないけど、存在することだけはわかる」ということがありえるんですね。
中間値の定理では、「連続」という条件は必ず必要です。これがないときは、実数解が存在するかどうはわかりません。

上のグラフのような場合がありえるからです。この場合は、 $x$ 軸と交わらないため、実数解の存在も言えません。途中でジャンプするようなことは、連続であることを仮定すれば起こりえません。
少し抽象的なのでどういうときに使うのかわかりにくいですが、「とにかく解が存在することだけを言いたい」場合にはよく使われます。次で実際の例を見てみます。
実数解が存在することの証明
$f(x)=\dfrac{1}{2^x}-x$ とすると、これは閉区間 $[0,1]$ で連続です。また、 $f(0)=1$, $f(1)=-\dfrac{1}{2}$ なので、異符号です。よって、中間値の定理から、\[ \dfrac{1}{2^x}-x=0 \]は、 $0\lt x \lt 1$ の範囲で、少なくとも1つの実数解をもつことがわかります。
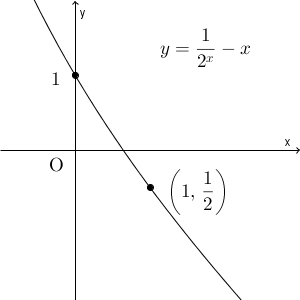
グラフは上のようになります。方程式の解は $x2^x=1$ を満たしますが、これがどんな値なのかはよくわかりません。しかし、これを満たす実数解が1つは存在する、ということはわかるんですね。
考えている閉区間で関数が連続であることと、両端での関数の値が違うことを確かめるだけで、実数解の存在が言える、というのは、抽象的な問題を考えるときなどで便利です。
おわりに
ここでは、中間値の定理について見てきました。グラフをイメージして理解するようにしましょう。連続であることは重要なので、確認し忘れないようにしましょう。





