【基本】三角形の内角の二等分線と比
ここでは三角形の内角の二等分線に関する性質について見ていきます。
内分
次のように、三角形 $\triangle \mathrm{ABC}$ の $\angle \mathrm{A}$ の二等分線を引きます。そして、辺 $\mathrm{BC}$ との交点を $\mathrm{D}$ とします。
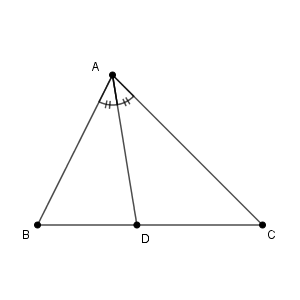
このとき、実は $\mathrm{BD:DC}=\mathrm{AB:AC}$ という関係式が成り立ちます(証明はこのページの中盤で行います)。
一般に、線分 $\mathrm{MN}$ 上の点 $\mathrm{P}$ が\[ \mathrm{MP:PN}=m:n \]を満たすとき($m,n$ は正の数)、点 $\mathrm{P}$ は線分 $\mathrm{MN}$ を $m:n$ に内分する、といいます。また、点 $\mathrm{P}$ のことを内分点といいます。
この用語を使うと、上で述べた性質は、「点 $\mathrm{D}$ は、辺 $\mathrm{BC}$ を $\mathrm{AB:AC}$ に内分する」と言い換えることができます。
三角形の内角の二等分線の性質の証明
それでは、冒頭で述べたことの証明をしていきます。2つの方法で示します。
まず1つ目の方法は、補助線を引く方法です。次のように、点 $\mathrm{C}$ を通り、線分 $\mathrm{AD}$ に平行な直線を引き、これと直線 $\mathrm{AB}$ との交点を $\mathrm{E}$ とします。
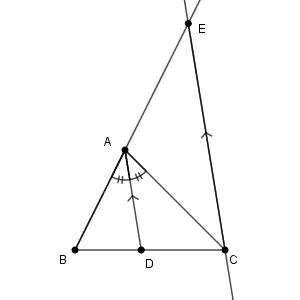
このとき、 $\triangle \mathrm{ABD}$ と $\triangle \mathrm{EBC}$ について、 $\angle \mathrm{B}$ が共通で、 $\angle \mathrm{BAD}=\angle \mathrm{BEC}$ (直線 $\mathrm{AD}$ と $\mathrm{CE}$ が平行より)だから、相似であることがわかります。よって、$\mathrm{BD:BC=BA:BE}$ より\[ \mathrm{BD:DC}=\mathrm{AB:AE} \]がわかります。
直線 $\mathrm{AD}$ と $\mathrm{CE}$ は平行であるから、錯角が等しいので\[ \angle \mathrm{CAD}=\angle \mathrm{ACE} \]です。また、そもそも $\mathrm{AD}$ は $\angle \mathrm{BAC}$ の二等分線なので、\[ \angle \mathrm{BAD}=\angle \mathrm{CAD} \]です。
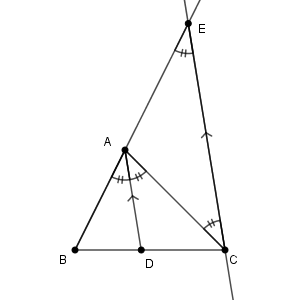
以上から $\angle \mathrm{ACE}=\angle \mathrm{AEC}$ が言えるので、 $\mathrm{AC=AE}$ が言えます。
よって、\[ \mathrm{BD:DC}=\mathrm{AB:AE}=\mathrm{AB:AC} \]となることがわかります。これで証明終わりです。
もう一つの方法は、三角比を使う方法です(参考:【基本】三角比と三角形の面積)。
$\triangle \mathrm{ABD}, \triangle \mathrm{ACD}$ は、直線 $\mathrm{BC}$ を底辺と考えると高さが共通なので、面積の比は $\mathrm{BD:DC}$ となります。

一方、三角比を使ってそれぞれの面積を表すと\[ \dfrac{\mathrm{AB\cdot AD}\sin\angle \mathrm{BAD}}{2}, \ \dfrac{\mathrm{AC\cdot AD}\sin\angle \mathrm{CAD}}{2} \]となります。ここで、直線 $\mathrm{AD}$ が $\angle \mathrm{A}$ の二等分線であったから、上の式に出てくる角は等しいので、面積比に着目すると
\begin{eqnarray}
& &
\mathrm{BD:DC} \\[5pt]
&=&
\dfrac{\mathrm{AB\cdot AD}\sin\angle \mathrm{BAD}}{2} : \dfrac{\mathrm{AC\cdot AD}\sin\angle \mathrm{CAD}}{2} \\[5pt]
&=&
\mathrm{AB}:\mathrm{AC}
\end{eqnarray}となることがわかります。これで証明終わりです。
内容をまとめておきます。
これを使って例題を解いてみましょう。
三角形の内角の二等分線の性質を使った例題
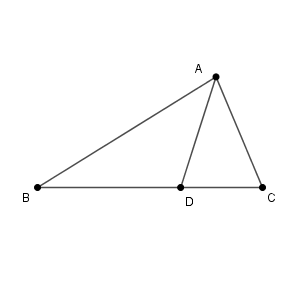
$\mathrm{AD}$ が $\angle \mathrm{A}$ の二等分線なので\[\mathrm{BD:DC}=\mathrm{AB:AC}=14:7=2:1\]です。なので\[ \mathrm{CD}=\frac{1}{2+1}\cdot \mathrm{BC}=5 \]となることがわかります。
おわりに
ここでは、三角形の内角の二等分線の性質について見てきました。線分の長さを求めるときに使うことがあるので、マスターしておきましょう。





