【基本】空間ベクトルの内積

ここでは、空間ベクトルの内積について見ていきます。

空間ベクトルの内積

【基本】ベクトルの内積 では、平面の場合で、ベクトルの内積を定義しました。空間ベクトルの場合も同じように定義します。

$\vec{0}$ でない2つのベクトル $\vec{a}$, $\vec{b}$ があるとします。

$\mathrm{O}$ を基準とし、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ となるように、 A, B をとります。また、 $\angle \mathrm{ AOB }$ を $\theta$ （ $0^{\circ} \leqq \theta \leqq 180^{\circ}$ ）とします。この $\theta$ のことを、 $\vec{a}$ と $\vec{b}$ のなす角、といいます。

このとき、 $|\vec{a}||\vec{b}|\cos\theta$ のことを、 $\vec{a}$ と $\vec{b}$ の内積(inner product) と呼び、 $\vec{a} \cdot \vec{b}$ で表します。

例えば、1辺の長さが $1$ の正四面体 $\mathrm{OABC}$ があったとします。

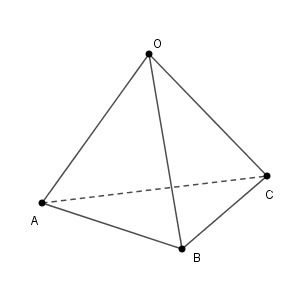
このとき
\begin{eqnarray} \overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} &=& 1\cdot 1\cdot \cos 60^{\circ} \\[5pt] &=& \frac{1}{2} \end{eqnarray}となります。

なお、 $\vec{a},\vec{b}$ のどちらかが $\vec{0}$ の場合、内積は $0$ とします。

空間ベクトルの内積と成分

先ほど空間ベクトルの内積を定義しましたが、一般的には空間の世界で「なす角」を考えるのは難しいことがあります（例えば、上の正四面体で、 $\mathrm{OA}$ と $\mathrm{BC}$ のなす角はパッとはわかりづらいです）。そこで役立つのが、内積を成分で表す方法です。平面のときでも、【基本】ベクトルの内積と成分で同じようなことをやっています。

$\vec{0}$ でない2つのベクトル $\vec{a}=(a_1,a_2,a_3)$, $\vec{b}=(b_1,b_2,b_3)$ があったとします。このときの内積 $\vec{a}\cdot\vec{b}$ を成分を使って表してみます。

$\mathrm{O}$ を基準とし、 $\vec{a}=\overrightarrow{\mathrm{OA}}$, $\vec{b}=\overrightarrow{\mathrm{OB}}$ となるように、空間内に点 $\mathrm{A,B}$ をとります。

$0^{\circ} \lt \theta \lt 180^{\circ}$ のとき、三角形 OAB に対して余弦定理が成り立つので、
\begin{eqnarray} \mathrm{ AB }^2 &=& \mathrm{ OA }^2+\mathrm{ OB }^2-2\mathrm{ OA }\cdot\mathrm{ OB }\cos\theta \end{eqnarray}が成り立ちます。なお、この式は $\theta=0^{\circ}$ のときも、 $\theta=180^{\circ}$ のときも成り立ちます。

よく見ると、最後の部分に内積が出てきています。 $\mathrm{ OA }\cdot\mathrm{ OB }\cos\theta$ というのは、ベクトルの言葉で書けば $|\vec{a}||\vec{b}|\cos\theta$ です。つまり、 $\vec{a}\cdot\vec{b}$ です。また、他の長さは、以下のように成分を使って書くことができます。
\begin{eqnarray} \mathrm{ AB }^2 &=& (b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2 \\[5pt] &=& a_1^2+a_2^2+a_3^2 +b_1^2+b_2^2+b_3^2 \\ & & -2(a_1b_1+a_2b_2+a_3b_3) \\[5pt] \mathrm{ OA }^2+\mathrm{ OB }^2 &=& a_1^2+a_2^2+a_3^2 +b_1^2+b_2^2+b_3^2 \\[5pt] \end{eqnarray}これらを使って共通する部分を削除すると\[ \vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3 \]となることがわかります。

各成分を掛けて足し合わせれば内積が求められる、というわけです。問題を解くときには、成分を使って内積を求め、角を求める、という使い方をよくします。

空間ベクトルの内積の性質

【基本】ベクトルの内積の性質では、平面の場合で、ベクトルの内積の性質を見ました。空間の場合も同じような性質が成り立ちます。

この交換法則は、どちらも $|\vec{a}||\vec{b}|\cos\theta$ と表されることからわかります。

これらは成分を使って地道に計算すれば、両辺が一致することが確かめられます。

例えば、先ほどの1辺の長さが $1$ の正四面体を考えてみます。

ここで、 $\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{BC}}$ は次のように計算できます。
\begin{eqnarray} \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{BC}} &=& \overrightarrow{\mathrm{OA}}\cdot \left( \overrightarrow{\mathrm{OC}} - \overrightarrow{\mathrm{OB}} \right) \\[5pt] &=& \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}} - \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}} \\[5pt] &=& 1\cdot 1\cdot \cos 60^{\circ} - 1\cdot 1\cdot \cos 60^{\circ} \\[5pt] &=& 0 \end{eqnarray}どちらも大きさは $0$ ではないので、なす角を $\theta$ とすれば $\cos\theta=0$ とわかります。つまり、 $\theta=90^{\circ}$ であり、 $\mathrm{OA}$ と $\mathrm{BC}$ は垂直であることがわかります。

このように、内積を使えば、角度に関する情報が求めやすくなるケースがあります。

おわりに

ここでは、空間ベクトルの内積について見てきました。平面のときでも、成分から内積を求め、内積から角度を求める、という使い方をよくしましたが、空間ベクトルでもこの使い方をよくします。空間のほうが角度を考えづらい場面が多いので、内積は強力なツールとなります。