【基本】三角形の外角の二等分線と比
ここでは三角形の外角の二等分線に関する性質について見ていきます。
外分
【基本】三角形の内角の二等分線と比では、三角形の内角の二等分線の性質を見ましたが、外角の二等分線も似たような性質をもっています。ここではそのことについて見ていきますが、その性質を見る前に、外分について説明しておきます。
次のように線分 $\mathrm{AB}$ があり、この線分の延長線上に点 $\mathrm{P}$ があるとします。
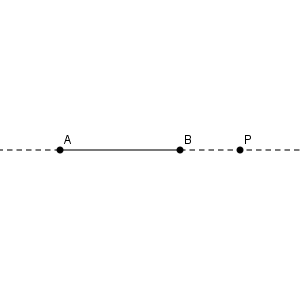
ここで、 $\mathrm{AP:PB}=m:n$ を満たすとき($m,n$ は異なる正の数)、点 $\mathrm{P}$ は線分 $\mathrm{AB}$ を $m:n$ に外分する、といいます。また、点 $\mathrm{P}$ のことを外分点といいます。
ちなみに、延長線上に点 $\mathrm{P}$ をとると、$\mathrm{AP\gt PB}$ か $\mathrm{AP\lt PB}$ のどちらかが成り立つので、 $1:1$ に外分する点というものはありません。
三角形の外角の二等分線の性質
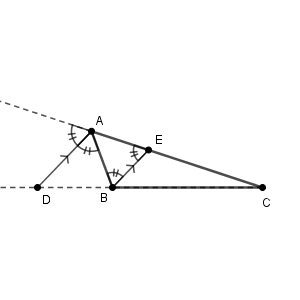
次のように、 $\mathrm{AB\gt AC}$ の三角形 $\mathrm{ABC}$ があるとします。$\angle \mathrm{A}$ の外角の二等分線と直線 $\mathrm{BC}$ との交点を $\mathrm{D}$ とします。
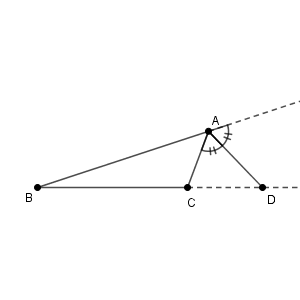
このとき、内角の二等分線の性質のところで見たのと同じ式\[ \mathrm{BD:DC}=\mathrm{AB:AC} \]が成り立ちます。以下では、この証明をしていきます。
次のように、点 $\mathrm{C}$ を通り、線分 $\mathrm{AD}$ に平行な直線を引き、これと直線 $\mathrm{AB}$ との交点を $\mathrm{E}$ とします。
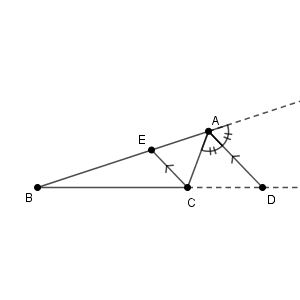
このとき、 $\triangle \mathrm{ABD}$ と $\triangle \mathrm{EBC}$ について、 $\angle \mathrm{B}$ が共通で、 $\angle \mathrm{BAD}=\angle \mathrm{BEC}$ (直線 $\mathrm{AD}$ と $\mathrm{CE}$ が平行より)だから、相似であることがわかります。よって、$\mathrm{BD:BC=BA:BE}$ より\[ \mathrm{BD:DC}=\mathrm{AB:AE} \]がわかります。
辺 $\mathrm{AB}$ の $\mathrm{A}$ 側の延長線上に点 $\mathrm{F}$ をとります。直線 $\mathrm{AD}$ と $\mathrm{CE}$ は平行であるから、錯角・同位角が等しいので
\begin{eqnarray}
\angle \mathrm{CAD} &=& \angle \mathrm{ACE} \\[5pt]
\angle \mathrm{AEC} &=& \angle \mathrm{FAD}
\end{eqnarray}となります。また、そもそも $\mathrm{AD}$ は $\angle \mathrm{FAC}$ の二等分線なので、\[ \angle \mathrm{FAD}=\angle \mathrm{CAD} \]です。
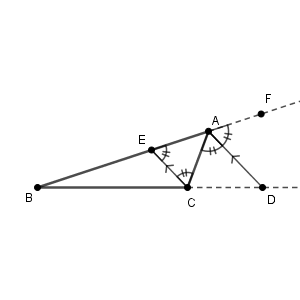
以上から $\angle \mathrm{ACE}=\angle \mathrm{AEC}$ なので、 $\mathrm{AC=AE}$ が言えます。
よって、\[ \mathrm{BD:DC}=\mathrm{AB:AE}=\mathrm{AB:AC} \]となることがわかります。これで証明終わりです。
$\mathrm{AB\lt AC}$ のときも、図が少し変わりますが、同じように示せます。
$\mathrm{AB}=\mathrm{AC}$ のときは、 $\angle \mathrm{A}$ の外角の二等分線が直線 $\mathrm{BC}$ と平行になってしまうため、交点が存在しません。そのため、この場合は除外しないといけません。
まとめると、次のようになります。
外分という用語を使えば、「点 $\mathrm{D}$ は辺 $\mathrm{BC}$ を $\mathrm{AB:AC}$ に外分する」と言い換えることができます。
この性質を使って例題を解いてみましょう。
三角形の外角の二等分線の性質を使った例題
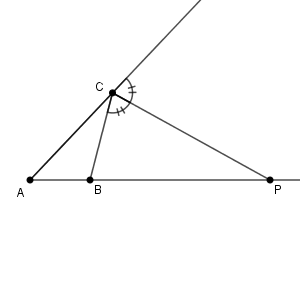
どのように適用するか、間違えないようにしましょう。
$\mathrm{CP}$ は $\angle \mathrm{C}$ の外角の二等分線なので\[\mathrm{AP:PB}=\mathrm{CA:CB}=4:3\]です。なので、$\mathrm{BP}=x$ とすると
\begin{eqnarray}
(x+2):x &=& 4:3 \\[5pt]
3(x+2) &=& 4x \\[5pt]
x &=& 6 \\[5pt]
\end{eqnarray}なので、$\mathrm{BP}=6$ と求められます。
おわりに
ここでは、三角形の外角の二等分線の性質について見てきました。内角のときと同じ式が出てきますが、どの線分を使うのかは内角のときより外角のときのほうが少し難しいです。どのように適用するか、間違えないようにしましょう。





