【基本】ユークリッドの互除法の使い方

【導入】ユークリッドの互除法 で書いた通り、「2つの大きな数の最大公約数を求める」には、結構計算が大変なんですよね。例えば、「$1649$ と $221$ の最大公約数は？」という問題を考えてみましょう。2で割れるか、3で割れるか、と小さい数字から順番に割っていってもいいのですが、それだと時間がかかってしまいます。

ユークリッドの互除法は、「数が大きすぎて、最大公約数を求めるのが大変だ」というときに使える技です。この技を知っていれば、大きな数がきても、最大公約数を求めるための計算量はグッと少なくなります。

詳しい原理については、別ページの【標準】ユークリッドの互除法の原理で説明するとして、このページでは、どのような発想を使っているのか、どうやって計算するのか、を説明していきます。

「ユークリッドの互除法」の発想

上にも書きましたが、次の問題を考えてみましょう。

この最大公約数を G とおくと、$1649$ は G で割り切れるし、 $221$ も G で割り切れますよね。ということは、この2つの差「$1649-221$」も $G$ で割り切れることがわかります。

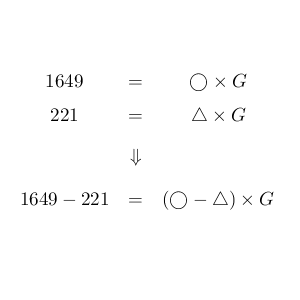
これをもっと進めていけば、$1649-221\times 2$ も $1649-221\times 3$ も $1649-221\times 4$ だって、$G$ で割り切れるはずです。

「$1649$ から $221$ を何度も引く」を進めていくと、割り算にたどり着きます。割り算をすると「$7$ 余り $102$」と計算できるので、\[ 1649 -221 \times 7 = 102 \]と書けることがわかります。この式で、 G で割り切れるものに注目してみましょう。

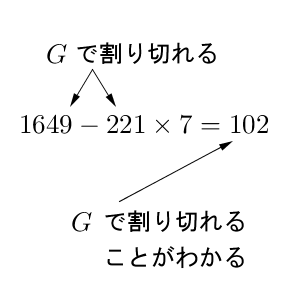
$1649$ も $221$ も G で割り切れるので、余りである $102$ も G で割り切れないといけません。

このような流れから、「割った余りとの最大公約数を考えればいいのではないか」という発想が生まれてきます。余りの方が小さい数になるので、考えやすくなりますよね。実際、 $1649$ と $221$ の最大公約数は、 $221$ と $102$ ($=1649$ を $221$ で割った余り) の最大公約数と同じになります。

厳密な証明は、【標準】ユークリッドの互除法の原理ですることにして、ここでは、「割った余りとの最大公約数を考えればいいんだな」ということだけおさえておけばOKです。

「ユークリッドの互除法」の具体的な計算方法

引き続き、「$1649$ と $221$ の最大公約数」について考えていきます。

先ほども書いた通り、「$1649$ と $221$ の最大公約数」を考えるには、割った余りとの最大公約数を考えればいいんでしたね。 $1649$ を $221$ で割った余りは、計算すると $102$ だとわかるので、「$221$ と $102$ の最大公約数」を考えればいいわけです。

実は、「ユークリッドの互除法」は繰り返し使うことができます。つまり、「$221$ と $102$ の最大公約数」を考えるには、「$102$ と、"$221$ を $102$ で割った余り"との最大公約数」を考えればOKなんです。

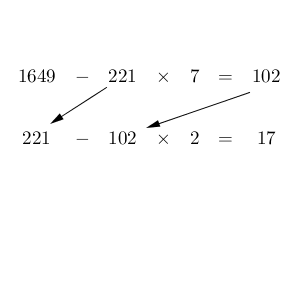
$221$ を $102$ で割った余りを計算すると $17$ だとわかるので、「$102$ と $17$の最大公約数」を考えればいい、ということです。

さらにさらに、もう一度繰り返してみます。今度は、 $102$ を $17$ で割った余りを考えてみます。すると、今回は割り切れてしまいます。これはどういうことかというと、「$102$ と $17$ の最大公約数」は $17$ である、ということなんですね。

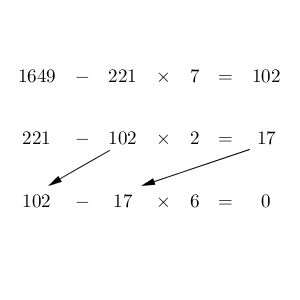
これを逆にたどっていくと、「$221$ と $102$ の最大公約数」も $17$ だし、「$1649$ と $221$ の最大公約数」も $17$ だとわかる。これが、ユークリッドの互除法の使い方です。

小さい数字から順番に割り切れるかどうかチェックすることなく、最大公約数を求めることができます。「余り」に注目するので、「ユークリッドの互除法」は、大きな数の最大公約数を考える場合に、大きな威力を発揮することがわかります。

おわりに

ここでは、ユークリッドの互除法に関する考え方と、具体的な計算方法を紹介しました。「割り算をして、余りとの最大公約数を考えていく」方法を繰り返し使えば、最大公約数が求められます。

このユークリッドの互除法に関する数学的な証明は、【標準】ユークリッドの互除法の原理でとりあげているので、そちらもぜひチェックしておきましょう。