【基本】連続関数
ここでは、連続関数や、その性質について見ていきます。
連続関数
【基本】関数の連続性では、関数がある点で連続であるとはどういうことかを見ました。関数 $f(x)$ に対し、 $x=a$ が定義域に含まれ、 $x\to a$ としたときに $f(x)$ が収束し、極限値が $f(a)$ となるときに、関数 $f(x)$ は $x=a$ で連続である、というのでした。グラフでいうと、 $x=a$ のまわりで、グラフがつながっていることに対応しているのでしたね。
「ある点で連続」であるだけでなく、定義域のどの点でも連続になっている関数もあります。例えば、 $y=x^2$ のグラフは、1つの曲線でつながっていて、途切れているところはないですね。このような関数のことを、連続関数(continuous function) といいます。
今までに見てきた関数のほとんどは連続関数なので、わざわざ「連続関数」という名前をつける必要性を感じられないかもしれません。しかし、それは今まで連続な関数が選ばれてきただけであって、運がよかった(?)だけなんですね。
今まで学んできた関数の中に、一次関数や二次関数や三次関数がありました。これらは、すべての実数で連続です。また、三角関数のうち、 $\sin x$ と $\cos x$ もすべての実数で連続です。指数関数 $f(x)=a^x$ もすべての実数で連続です(a は正で1以外の実数)。
無理関数 $f(x)=\sqrt{x}$ は、定義域は $x\geqq 0$ ですが、この範囲で連続です。 $x=0$ で連続かどうかは、 $x\to +0$ での極限だけをチェックして判断します。対数関数 $f(x)=\log_a x$ は、定義域が $x\gt 0$ で、この範囲で連続です。
分数関数 $f(x)=\dfrac{1}{x}$ は、定義域が $x\ne 0$ となります。 $x=0$ 以外では、グラフはつながっているので、この場合も定義域全体で連続です。三角関数の1つ、 $f(x)=\tan x$ は、 $x\ne \dfrac{2n-1}{2}\pi$ (n は整数) が定義域であり、この場合も定義域全体で連続となります。
実数全体が定義域の場合や、ある範囲だけが定義域の場合、いくつかの値以外が定義域の場合、いろんなケースがありますが、どんな場合でも、定義域で連続であれば、その関数は連続関数である、といいます。上に挙げた関数は、どれも、連続関数の例となっています。
また、連続関数を定数倍したもの、連続関数同士を足したり引いたり掛けたりしたもの、連続関数を別の連続関数(0となる場合を除く)で割ったものも、連続関数になります。
区間で連続
定義域全体で連続なら連続関数、という話をしましたが、「全体ではないけど、一部分だけなら連続」といいたいこともあります。
一般に、 $a\leqq x \leqq b$ を満たす $x$ の集合を閉区間(closed interval) といい、 $[a,b]$ で表します。また、 $a\lt x \lt b$ を満たす $x$ の集合を開区間(open interval) といい、 $(a,b)$ で表します。少しややこしいですが、この開区間を表す記号は、座標やベクトルの成分表示と見た目は同じですが、意味は全然違います。
この $[a,b]$ や $(a,b)$ での記号を使って、例えば $a\leqq x \lt b$ は $[a,b)$ と表します。また、 $x\geqq b$ は、 $[b,\infty)$ などと表します。 $\infty$ は数ではないので、 $[\ ,\ ]$ は使わずに $(\ ,\ )$ を使います。
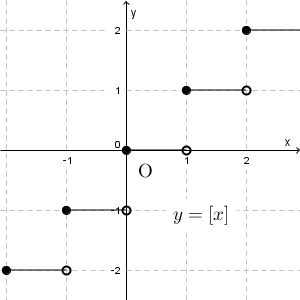
$f(x)=[x]$ のグラフは上のようになりますが、グラフが切れていることからもわかる通り、この関数は連続関数ではありません。しかし、 $[0,1)$ 内の各点では連続となります。このように、ある区間のすべての点で $f(x)$ が連続なら、 $f(x)$ はその区間で連続である、といいます。上の例であれば、 $f(x)=[x]$ は、区間 $[0,1)$ で連続である、といいます。また、 $x=1$ では連続でないので、区間 $[0,1]$ では連続でないことがわかります。
連続関数の性質
二次関数を学んだときに、最大値・最小値を求める問題をたくさん解きました。例えば、【基本】二次関数の最大・最小(定義域に制限あり)などです。二次関数の場合は、最大値・最小値を取りうるところは、頂点か区間の両端しかありませんでした。特に、区間の両端の点が定義域に含まれているかどうかは注意が必要でした。
一般に、閉区間で連続な関数について、次のことが成り立ちます。
高校の範囲では示すことができませんが、イメージとして理解できると思います。両端を含んだ区間で、グラフがつながっているのだから、どこかで最大値と最小値を持たないといけません。
条件にある「閉区間」と「連続」はどちらも重要です。どちらか1つでも欠けてはいけません。
$y=x^2\ (0\lt x\lt 1)$ は、連続な関数ですが、定義域が開区間です。 $y=0$, $y=1$ となることはないので、最大値も最小値も持っていません。
$y=x-2[x]-1\ (-1\leqq x \leqq 1)$ は、開区間ですが、連続ではありません。グラフは次のようになります。
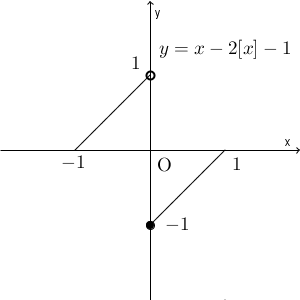
この場合は、 $y=1$ となることはないので、最大値をとりません。
このように、「閉区間」「連続」どちらの条件も必要で、これらを満たしていれば、最大値・最小値を持ちます。どちらか片方がない場合は、最大値を持つかどうか、最小値を持つかどうかは、決まりません。持つときもあるし、持たないときもあります。
おわりに
ここでは、連続関数について見てきました。今まで扱ってきた関数の大半は連続関数です。閉区間で連続なら最大値・最小値を持つ、という内容は、抽象的なので、これを使って入試問題を解くことは少ないでしょうが、数学的には重要な内容です。





