【基本】2曲線間の面積と積分

🕒 2017/11/28 🔄 2023/05/01

ここでは、2つの整式 $f(x),g(x)$ を使って、2つの曲線 $y=f(x)$ と $y=g(x)$ の間の部分の面積を、積分を使って求める方法を見ていきます。

📘 目次

面積と積分の復習

【基本】面積と整式の不定積分で見た内容を、もう一度振り返ってみましょう。

整式 $f(x)$ が $a\leqq x \leqq b$ のときに $f(x)\geqq 0$ を満たすとします。このとき、 $F(x)=\int f(x)dx$ とすると、 $x=a$, $x=b$, $y=f(x)$, x 軸で囲まれた部分の面積 S は、次のように表されるのでした。\[ S=F(b)-F(a) \]

これは、 $F(x)$ がどう変化するかを見れば、理解できるのでしたね。詳しくは上のリンク先にかいていますが、超特急で振り返ってみましょう。 $x=c$ から $x=c+h$ に変化したときに変化する面積は、 h が $0$ に近づいていくにつれて、横が $h$ で縦が $f(c)$ の長方形に近づいていくのでした。

\[ \lim_{h\to 0}\frac{F(c+h)-F(c)}{h}=f(c) \]となることから、「面積は不定積分の1つだ」ということがわかります。これと、「 $b=a$ のときの面積は $0$ 」ということから、\[ S=F(b)-F(a) \]が得られるのでした。

この式の右辺は、定積分で書くことができますね。つまり、次のようにまとめることができます。

面積と整式の定積分

整式 $f(x)$ は、 $a\leqq x \leqq b$ で、 $f(x)\geqq 0$ であるとする。このとき、 $x=a$, $x=b$, $y=f(x)$, x 軸で囲まれた部分の面積 S について、次が成り立つ。\[ S=\int_a^b f(x)dx \]

ここで、「 $f(x)\geqq 0$ 」という条件は重要です。この条件を外すとどうなるかは今後すぐに見ていきますが、その前に、2曲線の間の面積について考えていきましょう。

2曲線間の面積と積分

2つの整式 $f(x),g(x)$ が、 $a\leqq x \leqq b$ で、 $f(x)\geqq g(x)$ であるとします。このとき、 $x=a$, $x=b$ と $y=f(x)$, $y=g(x)$ で囲まれている部分の面積について考えていきましょう。

先ほどの「x 軸とで囲まれた部分の面積」を応用すればうまくいきそうですね。つまり、「 $x=a$, $x=b$, $y=f(x)$, x 軸で囲まれた部分」から「 $x=a$, $x=b$, $y=g(x)$, x 軸で囲まれた部分」を引けばいいですね。

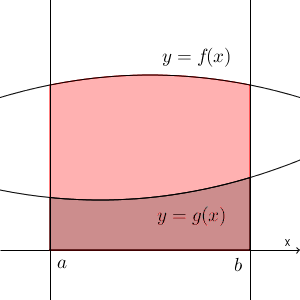
1つ注意点としては、「 $f(x)\geqq 0$, $g(x)\geqq 0$ 」が成り立つ場合でないと、上の性質は使えないということです。しかし、 x 軸より下の部分があっても、今の場合、問題をクリアすることができます。どちらも定数を足せばいいんですね。

つまり、もし、 x 軸より下の部分があれば、 $y=f(x)+k$ と $y=g(x)+k$ というように、両方を上にスライドすればいいわけです。こうすると、ともに x 軸より上にくるようにできます。

こうすれば、先ほどの性質が使える上、不要な k は以下の計算の通り、打ち消し合ってなくなります。
\begin{eqnarray} S &=& \int_a^b (f(x)+k) dx -\int_a^b (g(x)+k) dx \\[5pt] &=& \int_a^b \{ (f(x)+k)-(g(x)+k) \} dx \\[5pt] &=& \int_a^b \{ f(x)-g(x) \} dx \\[5pt] \end{eqnarray}結果的に、きれいな式が得られました。この式では、「 $f(x)\geqq 0$, $g(x)\geqq 0$ 」という条件は不要ですが、かわりに「 $f(x)\geqq g(x)$ 」という条件が必要になります。

2つの曲線で囲まれた部分の面積（整式）

整式 $f(x),g(x)$ は、 $a\leqq x \leqq b$ で、 $f(x)\geqq g(x)$ であるとする。このとき、 $x=a$, $x=b$, $y=f(x)$, $y=g(x)$ で囲まれた部分の面積 S について、次が成り立つ。\[ S=\int_a^b \{ f(x)-g(x) \} dx \]

文字で言うと、「上から下を引いて、左から右まで積分」すると、囲まれた部分の面積が出てくる、ということです。具体的な計算については別のページで見ますが、注意しないといけない点としては、「（考えている区間で）どちらの関数が上で、どちらの関数が下か」がわからないといけない、ということです。つまり、グラフをかいて考えないといけない、ということですね。