東京大学 理系 2025年度 第6問 解説
問題編
問題
複素数平面上の点 $\dfrac{1}{2}$ を中心とする半径 $\dfrac{1}{2}$ の円の周から原点を除いた曲線を $C$ とする。
(1) 曲線 $C$ 上の複素数 $z$ に対し、 $\dfrac{1}{z}$ の実部は $1$ であることを示せ。
(2) $\alpha,\beta$ を曲線 $C$ 上の相異なる複素数とするとき、 $\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}$ がとりうる範囲を複素数平面上に図示せよ。
(3) $\gamma$ を (2) で求めた範囲に属さない複素数とするとき、 $\dfrac{1}{\gamma}$ の実部がとりうる値の最大値と最小値を求めよ。
考え方
(1)はいいとして、(2)はハードです。(1)の「実部が $1$」を利用して計算していきましょう。やりかたはいろいろあると思います。
(3)はまた別の方向からの問題。二次曲線の性質を使って考えることもできますが、愚直に値を調べて行く方法でもできます。
解答編
問題
複素数平面上の点 $\dfrac{1}{2}$ を中心とする半径 $\dfrac{1}{2}$ の円の周から原点を除いた曲線を $C$ とする。
(1) 曲線 $C$ 上の複素数 $z$ に対し、 $\dfrac{1}{z}$ の実部は $1$ であることを示せ。
解答
(1)
$z=\dfrac{1}{2}+\dfrac{1}{2}(\cos\theta+i\sin\theta)$ と書ける($0\leqq \theta \lt \pi$, $\pi\lt\theta\lt 2\pi$)。よって、
\begin{eqnarray}
\frac{1}{z}
&=&
\frac{2}{1+\cos\theta+i\sin\theta} \\[5pt]
&=&
\frac{2(1+\cos\theta-i\sin\theta)}{(1+\cos\theta)^2+(\sin\theta)^2} \\[5pt]
&=&
\frac{2+2\cos\theta-2i\sin\theta}{2+2\cos\theta} \\[5pt]
&=&
1-i\frac{\sin\theta}{1+\cos\theta} \\[5pt]
&=&
1-i\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{2\cos^2\frac{\theta}{2}} \\[5pt]
&=&
1-i \tan\frac{\theta}{2} \\[5pt]
\end{eqnarray}なので、 $\dfrac{1}{z}$ の実部は $1$ である。(終)
解答編 つづき
問題
(2) $\alpha,\beta$ を曲線 $C$ 上の相異なる複素数とするとき、 $\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}$ がとりうる範囲を複素数平面上に図示せよ。
解答
(2)
(1)より、 $\dfrac{1}{z}=1-i \tan\dfrac{\theta}{2}$ で、 $\theta$ は $0\leqq \theta \lt \pi$, $\pi\lt\theta\lt 2\pi$ の範囲を動くので、虚部は実数全体を動く。
実数 $a,b$ を使って、$\dfrac{1}{\alpha}=1+ai$, $\dfrac{1}{\beta}=1+bi$ とかくと、 $\alpha,\beta$ が $C$ 上を $\alpha\ne\beta$ を満たしながら動くとき、 $a,b$ は $a\ne b$ を満たしながら実数全体を動く。このとき
\begin{eqnarray}
& &
\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2} \\[5pt]
&=&
(1+ai)^2+(1+bi)^2 \\[5pt]
&=&
2-a^2-b^2 +2(a+b)i \\[5pt]
\end{eqnarray}となる。ここで、この複素数を $x+yi$ と表す( $x,y$ は実数)と、\[ y=2(a+b) \]なので、 $y$ は実数全体を動く。また、
\begin{eqnarray}
x &=& 2-a^2-b^2 \\[5pt]
&=&
2-\frac{(a+b)^2+(a-b)^2}{2} \\[5pt]
&=&
2-\frac{y^2}{8}-\frac{(a-b)^2}{2}
\end{eqnarray}とかけ、 $a,b$ は $a\ne b$ を満たしながら動くので、\[ x \lt 2-\frac{y^2}{8} \]を満たしながら全体を動く。
よって、求める領域は以下の色付きの部分。ただし、境界線上の点は含まない。
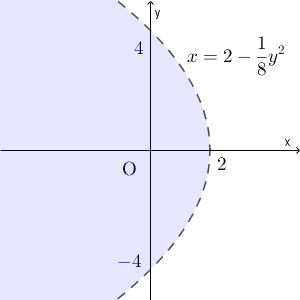
…(答)
解答編 つづき
問題
(3) $\gamma$ を (2) で求めた範囲に属さない複素数とするとき、 $\dfrac{1}{\gamma}$ の実部がとりうる値の最大値と最小値を求めよ。
解答
(3)
(2)より、 $\gamma=x+yi$ とかくと、
\begin{eqnarray}
x & \geqq & -\frac{1}{8}y^2+2 \\[5pt]
8x & \geqq & -y^2+16 \\[5pt]
y^2 & \geqq & -8x+16 \\[5pt]
\end{eqnarray}を満たす。また、
\begin{eqnarray}
\dfrac{1}{\gamma}
&=&
\frac{1}{x+yi} \\[5pt]
&=&
\frac{x-yi}{x^2+y^2} \\[5pt]
\end{eqnarray}なので、実部は\[ \frac{x}{x^2+y^2} \]である。よって、 $x\geqq -\frac{1}{8}y^2+2$ を満たしながら動くときの、この実部の最大値と最小値を求めればよい。
(a) $x\geqq 2$ のとき
$-8x+16\leqq 0$ なので、 $y^2 \geqq -8x+16$ はつねに成り立つ。つまり、$y$ は実数全体を動く。
よって、実部が最大となるのは、 $y=0$ のときであり、\[ \dfrac{x}{x^2+y^2}=\frac{1}{x} \]なので、 $\dfrac{1}{2}$ 以下であることがわかる。 $y$ はいくらでも大きくできるので、実部は $\dfrac{1}{2}$ 以下のすべての正の値をとる。
(b) $0\leqq x\leqq 2$ のとき
$y$ は $y^2 \geqq -8x+16$ を満たしながら動く。よって、実部が最大となるのは、 $y^2=-8x+16$ のときであり、
\begin{eqnarray}
\dfrac{x}{x^2+y^2}
&=&
\dfrac{x}{x^2-8x+16} \\[5pt]
&=&
\dfrac{x}{(x-4)^2} \\[5pt]
\end{eqnarray}とかける。 $0\leqq x\leqq 2$ のとき、分子は単調増加で、分母は単調減少でどちらも $0$ 以上なので、最大値をとるのは $x=2$ のときであり、その値は $\dfrac{1}{2}$ である。
$x=0$ のときに実部は $0$ で、実部は負になることはないので、実部は $0$ 以上 $\dfrac{1}{2}$ 以下のすべての値をとる。
(c) $x\lt 0$ のとき
$y$ は $y^2 \geqq -8x+16$ を満たしながら動く。今回は実部の分子が負なので、実部が最小となるのは、 $y^2=-8x+16$ のときとなる。その値は
\begin{eqnarray}
\dfrac{x}{x^2+y^2}
&=&
\dfrac{x}{x^2-8x+16} \\[5pt]
&=&
\dfrac{1}{x-8+\frac{16}{x}} \\[5pt]
\end{eqnarray}とかける。ここで、 $a=-x$ とすると、相加平均相乗平均の関係から\[ a+\frac{16}{a} \geqq 8 \]が成り立つ(等号は $a=4$ のときに成り立つ)。よって、\[ x-8+\frac{16}{x} \leqq -16 \]が成り立ち、両辺は負だから\[ -\dfrac{1}{16} \leqq \dfrac{1}{x-8+\frac{16}{x}} \]となるので、最小値は $-\dfrac{1}{16}$ となる。
$y$ はいくらでも大きくできるので、実部は $-\dfrac{1}{16}$ 以上のすべての負の値をとる。
(a)(b)(c)より、 $\dfrac{1}{\gamma}$ の実部は $-\dfrac{1}{16}$ 以上 $\dfrac{1}{2}$ 以下の値をすべてとるので、最大値は $\dfrac{1}{2}$ で、最小値は $-\dfrac{1}{16}$ となる。…(答)





