東京大学 理系 2025年度 第3問 解説
問題編
問題
平行四辺形 $\mathrm{ABCD}$ において、 $\angle\mathrm{ABC}=\dfrac{\pi}{6}$, $\mathrm{AB}=a$, $\mathrm{BC}=b$, $a\leqq b$ とする。次の条件を満たす長方形 $\mathrm{EFGH}$ を考え、その面積を $S$ とする。
条件:点 $\mathrm{A,B,C,D}$ はそれぞれ辺 $\mathrm{EF,FG,GH,HE}$ 上にある。
ただし、辺はその両端の点を含むものとする。
(1) $\angle\mathrm{BCG}=\theta$ とするとき、 $S$ を $a,b,\theta$ を用いて表せ。
(2) $S$ のとりうる値の最大値を $a,b$ を用いて表せ。
考え方
(1)はいいとして、(2)はまず $S$ をわかりやすい形に変形していきます。最大値を求めるには $\theta$ で微分するのがよくある流れですが、今の場合はさらに複雑になってしまいます。関数の形をうまく利用して、最大値を考えましょう。最大値をいつとるかで場合分けも必要となります。
解答編
問題
平行四辺形 $\mathrm{ABCD}$ において、 $\angle\mathrm{ABC}=\dfrac{\pi}{6}$, $\mathrm{AB}=a$, $\mathrm{BC}=b$, $a\leqq b$ とする。次の条件を満たす長方形 $\mathrm{EFGH}$ を考え、その面積を $S$ とする。
条件:点 $\mathrm{A,B,C,D}$ はそれぞれ辺 $\mathrm{EF,FG,GH,HE}$ 上にある。
ただし、辺はその両端の点を含むものとする。
(1) $\angle\mathrm{BCG}=\theta$ とするとき、 $S$ を $a,b,\theta$ を用いて表せ。
解答
(1)
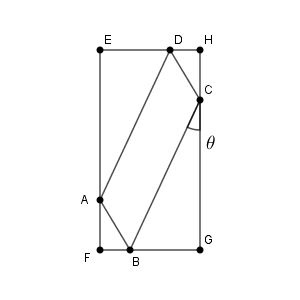
$\mathrm{CG}=b\cos\theta$, $\mathrm{BG}=b\sin\theta$ である。また、
\begin{eqnarray}
\angle\mathrm{ABF}
&=&
\pi-\frac{\pi}{6}-\left(\frac{\pi}{2}-\theta\right) \\[5pt]
&=&
\theta+\frac{\pi}{3}
\end{eqnarray}より、
\begin{eqnarray}
\mathrm{BF} &=& a\cos\left(\theta+\frac{\pi}{3}\right) \\[5pt]
\mathrm{CH} &=& \mathrm{AF} = a\sin\left(\theta+\frac{\pi}{3}\right) \\[5pt]
\end{eqnarray}となるので
\begin{eqnarray}
S
&=&
\mathrm{(BG+BF)\times(CG+CH)} \\[5pt]
&=&
\left(b\sin\theta +a\cos\left(\theta+\frac{\pi}{3}\right)\right) \left(b\cos\theta +a\sin\left(\theta+\frac{\pi}{3}\right)\right) \\[5pt]
\end{eqnarray}となる。(答)
解答編 つづき
問題
(2) $S$ のとりうる値の最大値を $a,b$ を用いて表せ。
解答
(2)
$0\leqq \theta\leqq \dfrac{\pi}{2}$ かつ $0\leqq \theta+\dfrac{\pi}{3}\leqq \dfrac{\pi}{2}$ より、 $\theta$ の動く範囲は $0\leqq \theta\leqq \dfrac{\pi}{6}$ である。なお、 $\theta=0$ のときは $\mathrm{BC}$ が $\mathrm{GH}$ 上にあるときで、 $\theta=\dfrac{\pi}{6}$ のときは $\mathrm{AB}$ が $\mathrm{EF}$ 上にあるときである。
(1)の $S$ を変形すると、
\begin{eqnarray}
S
&=&
\left(b\sin\theta +a\cos\left(\theta+\frac{\pi}{3}\right)\right) \left(b\cos\theta +a\sin\left(\theta+\frac{\pi}{3}\right)\right) \\[5pt]
&=&
b^2 \sin\theta\cos\theta
+a^2 \sin\left(\theta+\frac{\pi}{3}\right) \cos\left(\theta+\frac{\pi}{3}\right) \\
& &
+ab \left(\cos\theta\cos\left(\theta+\frac{\pi}{3}\right)+\sin\theta\sin\left(\theta+\frac{\pi}{3}\right)\right) \\[5pt]
&=&
\frac{b^2}{2} \sin 2\theta
+\frac{a^2}{2} \sin 2\left(\theta+\frac{\pi}{3}\right) \\
& &
+ab \cos \left\{ \theta -\left(\theta+\frac{\pi}{3}\right) \right\} \\[5pt]
&=&
\frac{b^2}{2} \sin 2\theta +\frac{a^2}{2} \sin \left(2\theta+\frac{2\pi}{3}\right) +\frac{ab}{2} \\[5pt]
&=&
\frac{b^2}{2} \sin 2\theta +\frac{a^2}{2} \left( \sin 2\theta \cos\frac{2}{3}\pi +\cos 2\theta \sin\frac{2}{3}\pi \right) +\frac{ab}{2} \\[5pt]
&=&
\frac{2b^2-a^2}{4} \sin 2\theta +\frac{a^2\sqrt{3}}{4}\cos 2\theta +\frac{ab}{2} \\[5pt]
\end{eqnarray}となる。
$\overrightarrow{\mathrm{OP}}=(\cos2\theta,\sin2\theta)$, $\overrightarrow{\mathrm{OQ}}=\left(\dfrac{a^2\sqrt{3}}{4},\dfrac{2b^2-a^2}{4}\right)$, $\mathrm{R}(1,0)$ とすると、\[ S=\overrightarrow{\mathrm{OP}}\cdot \overrightarrow{\mathrm{OQ}}+\frac{ab}{2} \]とかける。ここで、 $0\leqq \theta \leqq \dfrac{\pi}{6}$ より、 $0\leqq 2\theta \leqq \dfrac{\pi}{3}$ である。また、 $b\geqq a\gt 0$ より $2b^2-a^2\geqq 0$ だから、 $0\leqq \angle\mathrm{QOR}\leqq\dfrac{1}{2}\pi$ であり、
\begin{eqnarray}
& &
\frac{2b^2-a^2}{4} \div \frac{a^2\sqrt{3}}{4} \leqq \sqrt{3} \\[5pt]
&\iff&
2b^2-a^2 \leqq \sqrt{3}\cdot a^2\sqrt{3} \\[5pt]
&\iff&
b^2 \leqq 2a^2 \\[5pt]
&\iff&
b \leqq \sqrt{2}a \\[5pt]
\end{eqnarray}となる。これより、 $a\leqq b\leqq \sqrt{2}$ のときは $0\leqq\angle\mathrm{QOR}\leqq\dfrac{\pi}{3}$ であり、 $b\gt \sqrt{2}$ のときは $\angle\mathrm{QOR}\gt\dfrac{\pi}{3}$ であることがわかる。
(i) $a\leqq b\leqq \sqrt{2}a$
$\theta$ を動かすと、 $\overrightarrow{\mathrm{OP}}, \overrightarrow{\mathrm{OQ}}$ が同じ向きで平行になるときがあるので、そのときに $S$ は最大値をとる。よって、 $S$ の最大値は
\begin{eqnarray}
S
&=&
|\overrightarrow{\mathrm{OP}}| |\overrightarrow{\mathrm{OQ}}|+\frac{ab}{2} \\[5pt]
&=&
\sqrt{\frac{3a^4}{16} +\frac{4b^4-4a^2b^2+a^4}{16}}+\frac{ab}{2} \\[5pt]
&=&
\dfrac{\sqrt{a^4-a^2b^2+b^4}}{2}+\frac{ab}{2} \\[5pt]
\end{eqnarray}となる。
(ii) $b\gt \sqrt{2}a$ のとき
$\angle\mathrm{POQ}$ が一番小さいときに $S$ は最大値をとる。 $0\leqq 2\theta\leqq \dfrac{\pi}{3}$ で、 $\angle\mathrm{QOR}\gt\dfrac{\pi}{3}$ なので、 $S$ が最大値をとるのは、 $2\theta=\dfrac{\pi}{3}$ のときである。このときの $S$ は
\begin{eqnarray}
S
&=&
\frac{2b^2-a^2}{4} \sin 2\theta +\frac{a^2\sqrt{3}}{4}\cos 2\theta +\frac{ab}{2} \\[5pt]
&=&
\frac{2b^2-a^2}{4} \cdot\frac{\sqrt{3}}{2} +\frac{a^2\sqrt{3}}{4} \cdot\frac{1}{2} +\frac{ab}{2} \\[5pt]
&=&
\frac{\sqrt{3}}{4}b^2 +\frac{ab}{2} \\[5pt]
\end{eqnarray}である。
以上より、 $S$ の最大値は
$a\leqq b\leqq \sqrt{2}a$ のときは、 $\dfrac{\sqrt{a^4-a^2b^2+b^4}}{2}+\dfrac{ab}{2}$
$b\gt \sqrt{2}a$ のときは、 $\dfrac{\sqrt{3}}{4}b^2 +\dfrac{ab}{2}$
…(答)





