東京大学 理系 2025年度 第2問 解説
問題編
問題
(1) $x\gt 0$ のとき、不等式 $\log x\leqq x-1$ を示せ。
(2) 次の極限を求めよ。\[ \lim_{n\to\infty} n \int_1^2\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)dx \]
考え方
(1)はいいとして、問題は(2)です。(1)は(2)のヒントだと考えると、はさみうちを使うんだろうと予想できますが、(1)だけだとはさめません。もう片方は自分であみださないといけないので難しいです。 $\log x$ の性質を使って、下からの評価を考えましょう。(もしくは、誘導を完全に無視して考える方法もあります)
解答編
問題
(1) $x\gt 0$ のとき、不等式 $\log x\leqq x-1$ を示せ。
解答
(1)
$f(x)=(x-1)-\log x$ とすると\[ f'(x)=1-\frac{1}{x}=\frac{x-1}{x} \]なので、増減表は次のようになる。
\begin{array}{c|ccccc}
x & 0 & \cdots & 1 & \cdots \\
\hline
f'(x) & & - & 0 & + & \\
\hline
f(x) & & \searrow & 0 & \nearrow &
\end{array}よって、 $f(x)\geqq 0$ だから $\log x\leqq x-1$ が成り立つ。(終)
解答編 つづき
問題
(2) 次の極限を求めよ。\[ \lim_{n\to\infty} n \int_1^2\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)dx \]
解答
(2)
(1)より\[ \log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)\leqq \left(\frac{1+x^{\frac{1}{n}}}{2}\right)-1 =\frac{x^{\frac{1}{n}}-1}{2} \]が成り立つ。よって
\begin{eqnarray}
& &
n \int_1^2\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)dx \\[5pt]
& \leqq &
n \int_1^2 \frac{x^{\frac{1}{n}}-1}{2} dx \\[5pt]
& = &
\frac{n}{2} \left[ \frac{1}{\frac{1}{n}+1}x^{\frac{1}{n}+1} -x \right]_1^2 \\[5pt]
& = &
\frac{n}{2} \left\{ \frac{n}{1+n}(2^{\frac{1}{n}+1}-1) -(2-1) \right\} \\[5pt]
& = &
\frac{n}{2(1+n)} \left\{ n 2^{\frac{1}{n}+1}-n -(1+n) \right\} \\[5pt]
& = &
\frac{n}{2(1+n)} \left( n 2^{\frac{1}{n}+1}-2n -1 \right) \\[10pt]
& = &
\frac{n}{2(1+n)} \left( \frac{2^{\frac{1}{n}+1}-2^{0+1}}{\frac{1}{n}-0} -1 \right) \\[5pt]
\end{eqnarray}と変形できる。ここで、 $g(x)=2^{x+1}$ とすると、 $g'(x)=2^{x+1}\log 2$ なので、 $g'(0)=2\log 2$ である。よって、微分の定義から、
\begin{eqnarray}
& &
\lim_{n\to\infty} \frac{n}{2(1+n)} \left( \frac{2^{\frac{1}{n}+1}-2^{0+1}}{\frac{1}{n}-0} -1 \right) \\[5pt]
&=&
\frac{1}{2} \left( g'(0) -1 \right) \\[5pt]
&=&
\log 2 -\frac{1}{2} \\[5pt]
\end{eqnarray}となる。
一方、 $y=\log x$ は上に凸なので、一般に\[ \log\frac{p+q}{2} \geqq \frac{1}{2}\log p+\frac{1}{2}\log q \]が成り立つ。
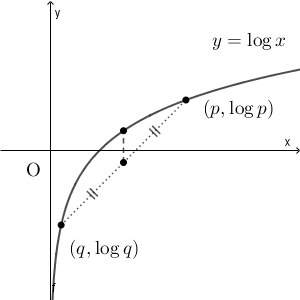
よって、 $p=1,q=x^{\frac{1}{n}}$ とすると、
\begin{eqnarray}
\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)
& \geqq &
\frac{1}{2} \log 1+\frac{1}{2}\log x^{\frac{1}{n}} \\[5pt]
& = &
\frac{1}{2n}\log x \\[5pt]
\end{eqnarray}だから
\begin{eqnarray}
& &
n \int_1^2\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)dx \\[5pt]
& \geqq &
n \int_1^2 \frac{1}{2n}\log x dx \\[5pt]
& = &
\frac{1}{2} \int_1^2 \log x dx \\[5pt]
& = &
\frac{1}{2} \Big[x\log x\Big]_1^2 -\frac{1}{2} \int_1^2 dx \\[5pt]
& = &
\frac{1}{2} \cdot 2\log 2 -\frac{1}{2} \\[5pt]
& = &
\log 2 -\frac{1}{2} \\[5pt]
\end{eqnarray}が成り立つ。
よって、はさみうちの原理から\[ \lim_{n\to\infty} n \int_1^2\log\left(\frac{1+x^{\frac{1}{n}}}{2}\right)dx=\log 2-\frac{1}{2} \]となる。(答)





