東京大学 理系 2024年度 第5問 解説
問題編
問題
座標空間内に3点 $\mathrm{A}(1,0,0)$, $\mathrm{B}(0,1,0)$, $\mathrm{C}(0,0,1)$ をとり、 $\mathrm{D}$ を線分 $\mathrm{AC}$ の中点とする。三角形 $\mathrm{ABD}$ の周および内部を $x$ 軸のまわりに1回転させて得られる立体の体積を求めよ。
考え方
立体を想像するのは難しいですが、求めるものは回転体の体積なので、切断して考えればいいです。どう切断するか、切断面はどうなっているかは考えやすいでしょう。断面積を求めるのに場合分けは必要ですが、必要な長さなどを求めるのはそんなに手間ではありません。
解答編
問題
座標空間内に3点 $\mathrm{A}(1,0,0)$, $\mathrm{B}(0,1,0)$, $\mathrm{C}(0,0,1)$ をとり、 $\mathrm{D}$ を線分 $\mathrm{AC}$ の中点とする。三角形 $\mathrm{ABD}$ の周および内部を $x$ 軸のまわりに1回転させて得られる立体の体積を求めよ。
解答
$\mathrm{D}$ の座標は $\left(\dfrac{1}{2},0,\dfrac{1}{2}\right)$ である。
立体と平面 $x=t$ とが共有点を持つのは、 $0\leqq t\leqq 1$ のときである。以下では、 $0\leqq t\leqq 1$ とする。
線分 $\mathrm{AB}$ は、$xy$ 平面上の直線 $y=1-x$ の一部なので、平面 $x=t$ と線分 $\mathrm{AB}$ との共有点の座標は、 $(t,1-t,0)$ である。
・$\dfrac{1}{2}\lt t \leqq 1$ のとき
三角形 $\mathrm{ABD}$ と平面 $x=t$ との共有点は、線分 $\mathrm{AD}$ 上にある。線分 $\mathrm{AD}$ は、$xz$ 平面上の直線 $z=1-x$ の一部なので、平面 $x=t$ と線分 $\mathrm{AD}$ との共有点の座標は、 $(t,0,1-t)$ である。
よって、三角形 $\mathrm{ABD}$ の周および内部を、平面 $x=t$ で切ったときの断面は次のようになる。
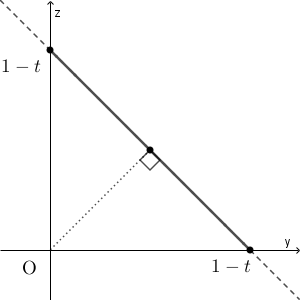
この線分は、平面 $x=t$ 上の直線 $z=-y+(1-t)$ のうち、 $0\leqq y\leqq 1-t$ の部分である。この線分上を点 $\mathrm{P}$ が動く場合、 $\mathrm{OP}$ が最大になるのは、 $y=0,1-t$ のときであり、その値は $1-t$ である。また、最小になるのは、 $y=\dfrac{1-t}{2}$ のときであり、その値は $\dfrac{1-t}{\sqrt{2}}$ である。 $\mathrm{OP}$ はこの間の値をすべてとる。
よって、立体を平面 $x=t$ で切ったときの断面は、点 $(t,0,0)$ を中心とする半径 $1-t$ の円から半径 $\dfrac{(1-t)}{\sqrt{2}}$ の円を除いた図形になるので、断面積は
\begin{eqnarray}
(1-t)^2\pi-\dfrac{(1-t)^2}{2}\pi=\dfrac{(t-1)^2}{2}\pi
\end{eqnarray}となる。
・$0\leqq t\leqq \dfrac{1}{2}$ のとき
三角形 $\mathrm{ABD}$ と平面 $x=t$ との共有点は、線分 $\mathrm{BD}$ 上にある。線分 $\mathrm{BD}$ 上の点の座標は、 $0\leqq s\leqq 1$ を満たす実数を使って
\begin{eqnarray}
& &
(0,1,0)+s\left\{\left(\frac{1}{2},0,\frac{1}{2}\right)-(0,1,0)\right\} \\[5pt]
&=&
\left(\frac{s}{2},1-s,\frac{s}{2}\right)
\end{eqnarray}とかける。 $x=t$ とすると、 $s=2t$ だから、線分 $\mathrm{BD}$ と平面 $x=t$ との共有点の座標は\[ (t,1-2t,t) \]であることがわかる。
ここで、 $(t,1-2t,t)$ は $z=-y+(1-t)$ を満たす。 $1-2t=t$ とすると、 $t=\dfrac{1}{3}$ である。
よって、 $\dfrac{1}{3}\leqq t\leqq \dfrac{1}{2}$ のとき、三角形 $\mathrm{ABD}$ の周および内部を、平面 $x=t$ で切ったときの断面は次のような線分になる。
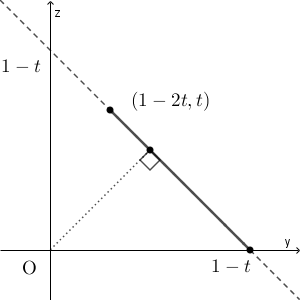
この線分上を点 $\mathrm{P}$ が動く場合、 $\mathrm{OP}$ が最大になるのは、 $y=1-t$ のときであり、最小になるのは、 $y=\dfrac{1-t}{2}$ のときだから、立体を平面 $x=t$ で切ったときの断面積は
\begin{eqnarray}
(1-t)^2\pi-\dfrac{(1-t)^2}{2}\pi=\dfrac{(t-1)^2}{2}\pi
\end{eqnarray}となる。
一方、 $0\leqq t\lt \dfrac{1}{3}$ のとき、三角形 $\mathrm{ABD}$ の周および内部を、平面 $x=t$ で切ったときの断面は次のような線分になる。
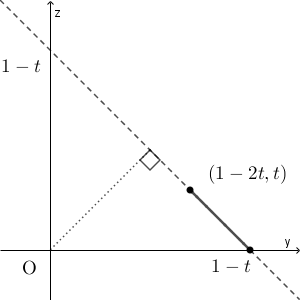
この線分上を点 $\mathrm{P}$ が動く場合、 $\mathrm{OP}$ が最大になるのは、 $y=1-t$ のときであり、最小になるのは、 $y=1-2t$ のときだから、立体を平面 $x=t$ で切ったときの断面積は
\begin{eqnarray}
& &
(1-t)^2\pi-\{(1-2t)^2+t^2\}\pi \\[5pt]
&=&
(t^2-2t+1)\pi-(4t^2-4t+1+t^2)\pi \\[5pt]
&=&
(-4t^2+2t)\pi \\[5pt]
\end{eqnarray}となる。
以上から、求める体積は
\begin{eqnarray}
& &
\int_{\frac{1}{3}}^1 \frac{(t-1)^2}{2}\pi dt
+\int_0^{\frac{1}{3}} (-4t^2+2t)\pi dt \\[5pt]
&=&
\pi\left[\frac{(t-1)^3}{6}\right]_{\frac{1}{3}}^1
+\pi\left[-\frac{4t^3}{3}+t^2\right]_0^{\frac{1}{3}} \\[5pt]
&=&
-\pi\cdot \frac{1}{6}\cdot\frac{-8}{27}
+\pi\left(-\frac{4}{3}\cdot\frac{1}{27}+\frac{1}{9}\right) \\[5pt]
&=&
\frac{4}{81}\pi
-\frac{4}{81}\pi+\frac{1}{9}\pi \\[5pt]
&=&
\frac{1}{9}\pi
\end{eqnarray}と求められる。
(答) $\dfrac{1}{9}\pi$





