東京大学 理系 2024年度 第3問 解説
問題編
問題
座標平面上を次の規則 (i), (ii) に従って、1秒ごとに動く点 $\mathrm{P}$ を考える。
(i) 最初に、 $\mathrm{P}$ は点 $(2,1)$ にいる。
(ii) ある時刻で $\mathrm{P}$ が点 $(a,b)$ にいるとき、その1秒後には $\mathrm{P}$ は
にいる。
- 確率 $\frac{1}{3}$ で $x$ 軸に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{3}$ で $y$ 軸に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{6}$ で直線 $y=x$ に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{6}$ で直線 $y=-x$ に関して $(a,b)$ と対称な点
以下の問いに答えよ。ただし、(1)については、結論のみを書けばよい。
(1) $\mathrm{P}$ がとりうる点の座標をすべて求めよ。
(2) $n$ を正の整数とする。最初から $n$ 秒後に $\mathrm{P}$ が点 $(2,1)$ にいる確率と、最初から $n$ 秒後に $\mathrm{P}$ が点 $(-2,-1)$ にいる確率は等しいことを示せ。
(3) $n$ を正の整数とする。最初から $n$ 秒後に $\mathrm{P}$ が点 $(2,1)$ にいる確率を求めよ。
考え方
点の数が多くて考えづらいです。書く分量も多くなってしまいます(パターンがあるので、ある程度は機械的に書けますが)。
(2)を解くと、いくつかの点をまとめて計算できるようになります。(3)は複数の漸化式を組み合わせて解いていきましょう。
解答編
問題
座標平面上を次の規則 (i), (ii) に従って、1秒ごとに動く点 $\mathrm{P}$ を考える。
(i) 最初に、 $\mathrm{P}$ は点 $(2,1)$ にいる。
(ii) ある時刻で $\mathrm{P}$ が点 $(a,b)$ にいるとき、その1秒後には $\mathrm{P}$ は
にいる。
- 確率 $\frac{1}{3}$ で $x$ 軸に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{3}$ で $y$ 軸に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{6}$ で直線 $y=x$ に関して $(a,b)$ と対称な点
- 確率 $\frac{1}{6}$ で直線 $y=-x$ に関して $(a,b)$ と対称な点
以下の問いに答えよ。ただし、(1)については、結論のみを書けばよい。
(1) $\mathrm{P}$ がとりうる点の座標をすべて求めよ。
解答
(1)
$\mathrm{P}$ が $(a,b)$ にいるとき、4種類の移動によって、それぞれ、$(a,-b)$, $(-a,b)$, $(b,a)$, $(-b,-a)$ に移動する。よって、これらの移動によって、 $x$ 座標と $y$ 座標を入れ替えたもの、および、$x$ 座標・$y$ 座標をそれぞれ $-1$ 倍した点のすべてに移動しうるので、 $\mathrm{P}$ がとりうる点の座標は、次の8点。
$(\pm2, \pm1)$, $(\pm1,\pm2)$ (複号任意)…(答)
解答編 つづき
問題
(2) $n$ を正の整数とする。最初から $n$ 秒後に $\mathrm{P}$ が点 $(2,1)$ にいる確率と、最初から $n$ 秒後に $\mathrm{P}$ が点 $(-2,-1)$ にいる確率は等しいことを示せ。
解答
(2)
(1)の答えの各点に、次のように 0 ~ 7 までの番号をつける。
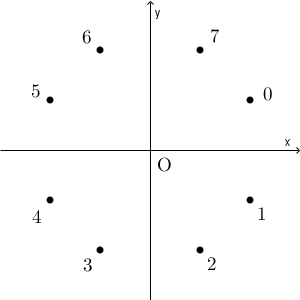
ある時刻で偶数番号の点にいるときは、それぞれの移動により、以下のように移動する。
1種類目の移動:0→1, 2→7, 4→5, 6→3
2種類目の移動:0→5, 2→3, 4→1, 6→7
3種類目の移動:0→7, 2→5, 4→3, 6→1
4種類目の移動:0→3, 2→1, 4→7, 6→5
いずれの場合も奇数番号の点に移動する。一方、奇数番号の点にいるときは、以下のように移動する。
1種類目の移動:1→0, 3→6, 5→4, 7→2
2種類目の移動:1→4, 3→2, 5→0, 7→6
3種類目の移動:1→6, 3→4, 5→2, 7→0
4種類目の移動:1→2, 3→0, 5→6, 7→4
いずれの場合も偶数番号の点に移動する。最初に 0 の点にいるので、最初から $n$ 秒後にいる場所は、 $n$ が奇数のときには奇数番号の点に必ずいて、 $n$ が偶数のときには偶数番号の点に必ずいることがわかる。
$n$ 秒後に、点 $i$ にいる確率を $p(n,i)$ と表す。以下では、すべての正の整数 $n$ について、
「 $p(n,0)=p(n,4)$, $p(n,1)=p(n,5)$, $p(n,2)=p(n,6)$, $p(n,3)=p(n,7)$ 」… (*)
となることを示す。
・$n=1$ のとき
$n$ は奇数なので、 $i=0,2,4,6$ に対し、 $p(1,i)=0$ である。また、$p(1,1)=p(1,5)$, $p(1,3)=p(1,7)$ なので、 $n=1$ のときに (*) が成り立つ。
・$n=k$ のときに (*) が成り立つとする。このとき、4種類の移動に分けて確率を計算すると
\begin{eqnarray}
p(k+1,0)=\frac{p(k,1)}{3}+\frac{p(k,5)}{3}+\frac{p(k,7)}{6}+\frac{p(k,3)}{6} \\[5pt]
p(k+1,4)=\frac{p(k,5)}{3}+\frac{p(k,1)}{3}+\frac{p(k,3)}{6}+\frac{p(k,7)}{6} \\[5pt]
\\
p(k+1,1)=\frac{p(k,0)}{3}+\frac{p(k,4)}{3}+\frac{p(k,6)}{6}+\frac{p(k,2)}{6} \\[5pt]
p(k+1,5)=\frac{p(k,4)}{3}+\frac{p(k,0)}{3}+\frac{p(k,2)}{6}+\frac{p(k,6)}{6} \\[5pt]
\\
p(k+1,2)=\frac{p(k,3)}{3}+\frac{p(k,7)}{3}+\frac{p(k,1)}{6}+\frac{p(k,5)}{6} \\[5pt]
p(k+1,6)=\frac{p(k,7)}{3}+\frac{p(k,3)}{3}+\frac{p(k,5)}{6}+\frac{p(k,1)}{6} \\[5pt]
\\
p(k+1,3)=\frac{p(k,2)}{3}+\frac{p(k,6)}{3}+\frac{p(k,0)}{6}+\frac{p(k,4)}{6} \\[5pt]
p(k+1,7)=\frac{p(k,6)}{3}+\frac{p(k,2)}{3}+\frac{p(k,4)}{6}+\frac{p(k,0)}{6} \\[5pt]
\end{eqnarray}
となるので、仮定から $n=k+1$ のときにも(*)が成り立つことがわかる。(2行ずつの式の右辺を見ると、1項目と3項目、2項目と4項目を入れ替えたものになっているので等しいことがわかる)
よって、数学的帰納法により、すべての正の整数 $n$ について(*)が成り立つ。 $p(n,0)=p(n,4)$ より、最初から $n$ 秒後に $\mathrm{P}$ が点 $(2,1)$ にいる確率と、最初から $n$ 秒後に $\mathrm{P}$ が点 $(-2,-1)$ にいる確率が等しいことが示せた。(終)
解答編 つづき
問題
(3) $n$ を正の整数とする。最初から $n$ 秒後に $\mathrm{P}$ が点 $(2,1)$ にいる確率を求めよ。
解答
(3)
(2)より、 $p(n,0)=p(n,4)$, $p(n,1)=p(n,5)$, $p(n,2)=p(n,6)$, $p(n,3)=p(n,7)$ である。また、(2)で示した、 $n=k+1$ と $n=k$ のときの関係式から
\begin{eqnarray}
p(n+1,0)=\frac{2}{3}p(n,1)+\frac{1}{3}p(n,3) \\[5pt]
p(n+1,1)=\frac{2}{3}p(n,0)+\frac{1}{3}p(n,2) \\[5pt]
p(n+1,2)=\frac{2}{3}p(n,3)+\frac{1}{3}p(n,1) \\[5pt]
p(n+1,3)=\frac{2}{3}p(n,2)+\frac{1}{3}p(n,0) \\[5pt]
\end{eqnarray}が成り立つ。
1つ目から3つ目を引き、2つ目から4つ目を引くと
\begin{eqnarray}
p(n+1,0)-p(n+1,2)=\frac{1}{3} (p(n,1)-p(n,3)) \\[5pt]
p(n+1,1)-p(n+1,3)=\frac{1}{3} (p(n,0)-p(n,2)) \\[5pt]
\end{eqnarray}が得られる。これより、\[ p(n+2,0)-p(n+2,2)=\frac{1}{9} (p(n,0)-p(n,2)) \]が成り立つことがわかる。
(2)で見たように、 $n$ が奇数の場合、 $p(n,0)=0$ である。 $n$ が偶数のとき、 $p(n,1)=p(n,3)=0$ なので、\[ p(n,0)+p(n,2)=\frac{1}{2} \]である。ここで、 $p(1,1)=p(1,5)=\dfrac{1}{3}$, $p(1,3)=p(1,7)=\dfrac{1}{6}$ なので
\begin{eqnarray}
p(2,0) &=& \frac{1}{9}+\frac{1}{9}+\frac{1}{36}+\frac{1}{36}=\frac{5}{18} \\[5pt]
p(2,2) &=& \frac{1}{18}+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}=\frac{4}{18} \\[5pt]
p(2,0)-p(2,2) &=& \frac{1}{18}
\end{eqnarray}であるから、\[ p(n,0)-p(n,2)=\left(\frac{1}{9}\right)^{\frac{n}{2}-1}\cdot\frac{1}{18}=\frac{1}{2}\cdot\frac{1}{3^n} \]となる。以上より、\[ p(n,0)=\frac{1}{4}+\frac{1}{4}\cdot \frac{1}{3^n} \]となる。
以上から、求める確率は
$n$ が奇数のとき、 $0$
$n$ が偶数のとき、 $\dfrac{1}{4}+\dfrac{1}{4}\cdot \dfrac{1}{3^n}$
となる。(答)





