共通テスト 数学II・数学B・数学C 2026年度 第7問 解説
【第4問~第7問から3問選択】
問題編
問題
$z$ を $0$ でない複素数とし、$w = z + \dfrac{1}{z}$ とする。また、$r$ を正の実数とし、複素数平面上で、原点 $\mathrm{O}$ を中心とする半径 $r$ の円を $C$ とする。
(1) $z = \sqrt{3} + i$ のとき、$|z| = \myBox{ア}$ であり
\[ w = \dfrac{\myBox{イ}\sqrt{\myBox{ウ}}}{\myBox{エ}} + \dfrac{\myBox{オ}}{\myBox{カ}}i \]である。(2) $z$ が $C$ 上を動くとき、$w$ が複素数平面上で描く図形を考える。
実数 $\theta$ を $z$ の偏角とし、極形式を用いて $z = r(\cos \theta + i \sin \theta)$ と表す。(i) $w = z + \dfrac{1}{z}$ を $r, \theta$ を用いて表すと
\[ w = \dBox{キ} + i \dBox{ク} \quad \cdots\cdots \text{①} \]である。したがって、$\theta$ の値によらず $\dbox{ク} = 0$ となるような $r$ の値は $\myBox{ケ}$ である。$\dbox{キ}$ 、$\dbox{ク}$ の解答群(同じものを繰り返し選んでもよい。)
0: $2r \cos \theta$
1: $2r \sin \theta$
2: $(r+1) \cos \theta$
3: $(r+1) \sin \theta$
4: $(r-1) \cos \theta$
5: $(r-1) \sin \theta$6: $\left( r + \dfrac{1}{r} \right) \cos \theta$
7: $\left( r + \dfrac{1}{r} \right) \sin \theta$
8: $\left( r - \dfrac{1}{r} \right) \cos \theta$
9: $\left( r - \dfrac{1}{r} \right) \sin \theta$
(ii) $r = \mybox{ケ}$ とする。$z$ が $C$ 上を動くとき、$w$ が描く図形は $\dBox{コ}$ である。
$\dbox{コ}$ については、最も適当なものを、次の0~5のうちから一つ選べ。
(iii) $r \neq \mybox{ケ}$ とする。$x, y$ を実数として $w = x + yi$ とおくと、① から
\[ x = \dbox{キ}, \quad y = \dbox{ク} \quad \cdots\cdots \text{②} \]が成り立つ。② の二つの式から $\theta$ を消去すると、$x, y$ は $\dBox{サ}$ を満たし、$z$ が $C$ 上を動くとき、$w = x + yi$ は $\dbox{サ}$ の表す図形を描く。$\dbox{サ}$ の解答群
0: $\dfrac{x^2}{r^2} + \dfrac{y^2}{r^2} = 1$
1: $\dfrac{x^2}{r^2} - \dfrac{y^2}{r^2} = 1$
2: $\dfrac{x^2}{\left( r + \dfrac{1}{r} \right)^2} + \dfrac{y^2}{\left( r - \dfrac{1}{r} \right)^2} = 1$
3: $\dfrac{x^2}{\left( r + \dfrac{1}{r} \right)^2} - \dfrac{y^2}{\left( r - \dfrac{1}{r} \right)^2} = 1$
4: $\dfrac{x^2}{\left( r - \dfrac{1}{r} \right)^2} + \dfrac{y^2}{\left( r + \dfrac{1}{r} \right)^2} = 1$
5: $\dfrac{x^2}{\left( r - \dfrac{1}{r} \right)^2} - \dfrac{y^2}{\left( r + \dfrac{1}{r} \right)^2} = 1$
(3) $r \neq \mybox{ケ}$ とする。$z$ が $C$ 上を動くとき、$w^2$ が描く図形を考えよう。
(i) $w^2$ を $z$ を用いて表すと、$w^2 = \dBox{シ}$ である。
$\dbox{シ}$ の解答群
0: $z^2 + \dfrac{1}{z^2}$
1: $z^2 + \dfrac{1}{z^2} + 1$
2: $z^2 + \dfrac{1}{z^2} - 1$
3: $z^2 + \dfrac{1}{z^2} + 2$
4: $z^2 + \dfrac{1}{z^2} - 2$
5: $z^2 + \dfrac{1}{z^2} + 2i$
(ii) $z$ が $C$ 上を動くとき、$z^2 + \dfrac{1}{z^2}$ が描く図形の方程式を考える。このとき、$z^2$ は原点 $\mathrm{O}$ を中心とする半径 $r^2$ の円を描く。このことから、$X, Y$ を実数として $z^2 + \dfrac{1}{z^2} = X + Yi$ とおくと、$X, Y$ は $\dBox{ス}$ を満たす。以上を踏まえると、$w^2$ が描く図形は $\dBox{セ}$ であることがわかる。
$\dbox{ス}$ の解答群
0: $\dfrac{X}{r^2 + \dfrac{1}{r^2}} + \dfrac{Y}{r^2 - \dfrac{1}{r^2}} = 1$
1: $\dfrac{X^2}{r^4} + \dfrac{Y^2}{r^4} = 1$
2: $\dfrac{X^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} + \dfrac{Y^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} = 1$
3: $\dfrac{X^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} - \dfrac{Y^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} = 1$
4: $\dfrac{X^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} + \dfrac{Y^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} = 1$
5: $\dfrac{X^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} - \dfrac{Y^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} = 1$
$\dbox{セ}$ については、最も適当なものを、次の0~7のうちから一つ選べ。
考え方
問題文に従って進んでいけば、途中でつまるところはほとんどないでしょう。最後の問題はさすがに少し考えないといけないところはあるものの、途中で細かい計算もほとんど出てこないですし、かなり解きやすい問題となっています。
【第4問~第7問から3問選択】
解答編
問題
$z$ を $0$ でない複素数とし、$w = z + \dfrac{1}{z}$ とする。また、$r$ を正の実数とし、複素数平面上で、原点 $\mathrm{O}$ を中心とする半径 $r$ の円を $C$ とする。
(1) $z = \sqrt{3} + i$ のとき、$|z| = \myBox{ア}$ であり
\[ w = \dfrac{\myBox{イ}\sqrt{\myBox{ウ}}}{\myBox{エ}} + \dfrac{\myBox{オ}}{\myBox{カ}}i \]である。
解説
(1)
\[ |z|=\sqrt{(\sqrt{3})^2+1^2}=2 \]
であり
\begin{eqnarray}
w
&=&
\sqrt{3}+i+\frac{1}{\sqrt{3}+i} \\[5pt]
&=&
\sqrt{3}+i+\frac{\sqrt{3}-i}{3+1} \\[5pt]
&=&
\frac{5\sqrt{3}}{4}+\frac{3}{4}i \\[5pt]
\end{eqnarray}となります。
解答
ア:2 (2点)
イウエオカ:53434 (2点)
解答編 つづき
問題
(2) $z$ が $C$ 上を動くとき、$w$ が複素数平面上で描く図形を考える。
実数 $\theta$ を $z$ の偏角とし、極形式を用いて $z = r(\cos \theta + i \sin \theta)$ と表す。(i) $w = z + \dfrac{1}{z}$ を $r, \theta$ を用いて表すと
\[ w = \dBox{キ} + i \dBox{ク} \quad \cdots\cdots \text{①} \]である。したがって、$\theta$ の値によらず $\dbox{ク} = 0$ となるような $r$ の値は $\myBox{ケ}$ である。$\dbox{キ}$ 、$\dbox{ク}$ の解答群(同じものを繰り返し選んでもよい。)
0: $2r \cos \theta$
1: $2r \sin \theta$
2: $(r+1) \cos \theta$
3: $(r+1) \sin \theta$
4: $(r-1) \cos \theta$
5: $(r-1) \sin \theta$6: $\left( r + \dfrac{1}{r} \right) \cos \theta$
7: $\left( r + \dfrac{1}{r} \right) \sin \theta$
8: $\left( r - \dfrac{1}{r} \right) \cos \theta$
9: $\left( r - \dfrac{1}{r} \right) \sin \theta$
解説
(2)(i)
\begin{eqnarray}
w
&=&
r(\cos\theta+i\sin\theta)+\frac{1}{r(\cos\theta+i\sin\theta)} \\[5pt]
&=&
r(\cos\theta+i\sin\theta)+\frac{\cos\theta-i\sin\theta}{r} \\[5pt]
&=&
\left(r+\frac{1}{r}\right)\cos\theta +i \left(r-\frac{1}{r}\right)\sin\theta
\end{eqnarray}
と計算できます。
なので、 $\theta$ の値によらず虚部が $0$ となるのは、 $r-\dfrac{1}{r}=0$ のときです。 $r\gt 0$ なので、 $r=1$ のときだとわかります。
解答
キク:69 (2点)
ケ:1 (1点)
解答編 つづき
問題
(ii) $r = \mybox{ケ}$ とする。$z$ が $C$ 上を動くとき、$w$ が描く図形は $\dBox{コ}$ である。
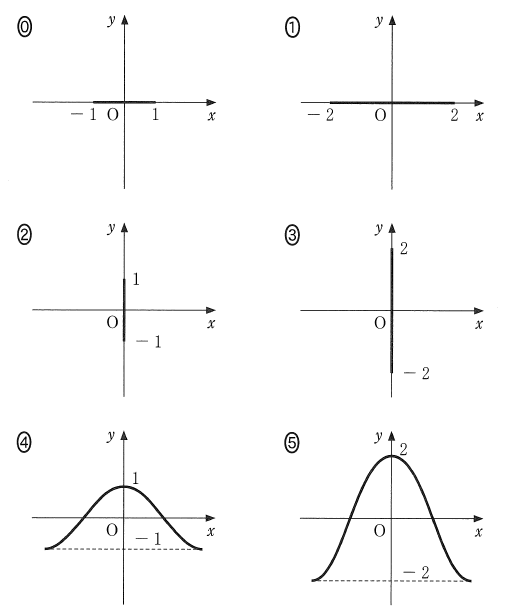
$\dbox{コ}$ については、最も適当なものを、次の0~5のうちから一つ選べ。
解説
(2)(ii)
$r=1$ のとき
\[ w = \left(r+\frac{1}{r}\right)\cos\theta +i \left(r-\frac{1}{r}\right)\sin\theta =2\cos\theta \]なので、 $\theta$ が動くと、虚部は $0$ のままで、実部が $-2$ から $2$ の範囲を動きます。なので選択肢1が答えだとわかります。
解答
コ:1 (2点)
解答編 つづき
問題
(iii) $r \neq \mybox{ケ}$ とする。$x, y$ を実数として $w = x + yi$ とおくと、① から
\[ x = \dbox{キ}, \quad y = \dbox{ク} \quad \cdots\cdots \text{②} \]が成り立つ。② の二つの式から $\theta$ を消去すると、$x, y$ は $\dBox{サ}$ を満たし、$z$ が $C$ 上を動くとき、$w = x + yi$ は $\dbox{サ}$ の表す図形を描く。$\dbox{サ}$ の解答群
0: $\dfrac{x^2}{r^2} + \dfrac{y^2}{r^2} = 1$
1: $\dfrac{x^2}{r^2} - \dfrac{y^2}{r^2} = 1$
2: $\dfrac{x^2}{\left( r + \dfrac{1}{r} \right)^2} + \dfrac{y^2}{\left( r - \dfrac{1}{r} \right)^2} = 1$
3: $\dfrac{x^2}{\left( r + \dfrac{1}{r} \right)^2} - \dfrac{y^2}{\left( r - \dfrac{1}{r} \right)^2} = 1$
4: $\dfrac{x^2}{\left( r - \dfrac{1}{r} \right)^2} + \dfrac{y^2}{\left( r + \dfrac{1}{r} \right)^2} = 1$
5: $\dfrac{x^2}{\left( r - \dfrac{1}{r} \right)^2} - \dfrac{y^2}{\left( r + \dfrac{1}{r} \right)^2} = 1$
解説
(2)(iii)
$r\ne 1$ のとき、 $w=x+yi$ とおくと、 $x=\left(r+\dfrac{1}{r}\right)\cos\theta$ で、 $y=\left(r-\dfrac{1}{r}\right)\sin\theta$ となります。 $\cos^2\theta+\sin^2\theta=1$ に代入すると\[ \frac{x^2}{\left(r+\dfrac{1}{r}\right)^2}+\frac{y^2}{\left(r-\dfrac{1}{r}\right)^2} = 1 \]を満たします。
解答
サ:2 (2点)
解答編 つづき
問題
(3) $r \neq \mybox{ケ}$ とする。$z$ が $C$ 上を動くとき、$w^2$ が描く図形を考えよう。
(i) $w^2$ を $z$ を用いて表すと、$w^2 = \dBox{シ}$ である。
$\dbox{シ}$ の解答群
0: $z^2 + \dfrac{1}{z^2}$
1: $z^2 + \dfrac{1}{z^2} + 1$
2: $z^2 + \dfrac{1}{z^2} - 1$
3: $z^2 + \dfrac{1}{z^2} + 2$
4: $z^2 + \dfrac{1}{z^2} - 2$
5: $z^2 + \dfrac{1}{z^2} + 2i$
解説
(3)(i)
\[ w^2=\left(z+\frac{1}{z}\right)^2=z^2+\frac{1}{z^2}+2 \]となります。
解答
シ:3 (1点)
解答編 つづき
問題
(ii) $z$ が $C$ 上を動くとき、$z^2 + \dfrac{1}{z^2}$ が描く図形の方程式を考える。このとき、$z^2$ は原点 $\mathrm{O}$ を中心とする半径 $r^2$ の円を描く。このことから、$X, Y$ を実数として $z^2 + \dfrac{1}{z^2} = X + Yi$ とおくと、$X, Y$ は $\dBox{ス}$ を満たす。以上を踏まえると、$w^2$ が描く図形は $\dBox{セ}$ であることがわかる。
$\dbox{ス}$ の解答群
0: $\dfrac{X}{r^2 + \dfrac{1}{r^2}} + \dfrac{Y}{r^2 - \dfrac{1}{r^2}} = 1$
1: $\dfrac{X^2}{r^4} + \dfrac{Y^2}{r^4} = 1$
2: $\dfrac{X^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} + \dfrac{Y^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} = 1$
3: $\dfrac{X^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} - \dfrac{Y^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} = 1$
4: $\dfrac{X^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} + \dfrac{Y^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} = 1$
5: $\dfrac{X^2}{\left( r^2 - \dfrac{1}{r^2} \right)^2} - \dfrac{Y^2}{\left( r^2 + \dfrac{1}{r^2} \right)^2} = 1$
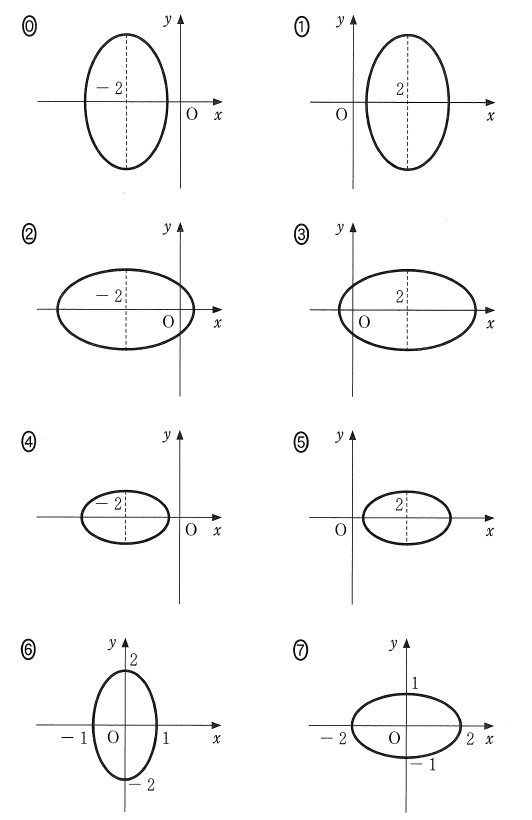
$\dbox{セ}$ については、最も適当なものを、次の0~7のうちから一つ選べ。
解説
(3)(ii)
$z^2=r^2(\cos2\theta+i\sin2\theta)$ なので、問題文にある通り、 $z^2$ は半径 $r^2$ の円を描くことがわかります。
(2)(iii)でみたように、 $z$ が半径 $r$ の円を動くとき、 $w=z+\dfrac{1}{z}$ は \[\frac{x^2}{\left(r+\dfrac{1}{r}\right)^2}+\frac{y^2}{\left(r-\dfrac{1}{r}\right)^2} = 1\]の表す図形を描くのだから、もし半径 $r^2$ の円を動くなら、 $z^2+\dfrac{1}{z^2}$ が描く図形は、先ほどの式の $r$ を $r^2$ に置き換えて、 $x$ を $X$ に、 $y$ を $Y$ に置き換えた式\[ \frac{X^2}{\left(r^2+\dfrac{1}{r^2}\right)^2}+\frac{Y^2}{\left(r^2-\dfrac{1}{r^2}\right)^2} = 1 \]の表す図形を描くことになります。 $w^2=z^2+\dfrac{1}{z^2}+2$ なので、 $w^2$ の描く図形は、これをさらに $2$ だけ右にずらした図形となります。
では、この図形がどんな図形なのか、選択肢から絞っていきましょう。まず、\[ \frac{x^2}{\left(r^2+\dfrac{1}{r^2}\right)^2}+\frac{y^2}{\left(r^2-\dfrac{1}{r^2}\right)^2} = 1 \]を考えます。この式は楕円の式です。この式で、 $y=0$ とすると、 $x^2=\left(r^2+\dfrac{1}{r^2}\right)^2$ なので、 $x=\pm \left(r^2+\dfrac{1}{r^2}\right)$ となります。また、 $x=0$ とすると、 $y=\pm \left(r^2-\dfrac{1}{r^2}\right)$ となります。 $r^2+\dfrac{1}{r^2} \gt r^2-\dfrac{1}{r^2}$ なので、横に長い楕円だとわかります。なので、答えは、横に長い楕円を $2$ だけ右にずらした図形なので、選択肢3か選択肢5に絞ることができます。(縦横の縮尺がわからないので、選択肢1の可能性もありえますが、あとで不適切だとわかります)
選択肢3と選択肢5では、 $y$ 軸と交わるかどうかが違っています。これは楕円の横幅の長さに注目すればわかります。相加平均・相乗平均の関係から\[ r^2+\dfrac{1}{r^2} \geqq 2 \]が成り立ちます。等号が成り立つのは $r=1$ のとき( $r$ は正の実数なので)ですが、今は $r\ne 1$ のときを考えているのだから、上の不等号の等式が成り立つことはないとわかります。つまり、\[ r^2+\dfrac{1}{r^2}\gt 2 \] なので、右に $2$ だけずらしても、 $y$ 軸と交わることがわかります。こうして、選択肢3 が答えだとわかります。
解答
ス:2 (2点)
ソ:3 (2点)