共通テスト 数学II・数学B・数学C 2026年度 第6問 解説
【第4問~第7問から3問選択】
問題編
問題
平面上に、$\triangle \mathrm{ABC}$ と点 $\mathrm{M}$ がある。
(1) 次の等式を満たす点 $\mathrm{P}$ を考える。
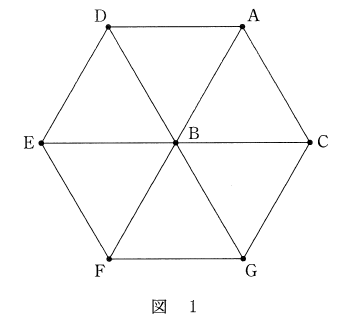
\[ \overrightarrow{\mathrm{MP}} = \overrightarrow{\mathrm{MA}} + 2\overrightarrow{\mathrm{MB}} - \overrightarrow{\mathrm{MC}} \quad \cdots\cdots \text{①} \]3点 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ を図1の位置にとる。ただし、図1における $\triangle \mathrm{ABC}$ は正三角形、六角形 $\mathrm{DEFGCA}$ は正六角形である。
・$\mathrm{M}$ が $\mathrm{A}$ と一致するとき、$\mathrm{P}$ は $\dBox{ア}$ と一致する。
・$\mathrm{M}$ が $\mathrm{D}$ と一致するとき、$\mathrm{P}$ は $\dBox{イ}$ と一致する。
$\dbox{ア}$ 、$\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\mathrm{A}$
1: $\mathrm{B}$
2: $\mathrm{C}$
3: $\mathrm{D}$
4: $\mathrm{E}$
5: $\mathrm{F}$
6: $\mathrm{G}$(2) $a, b, c$ を実数とする。次の等式を満たす点 $\mathrm{P}$ を考える。
\[ \overrightarrow{\mathrm{MP}} = a\overrightarrow{\mathrm{MA}} + b\overrightarrow{\mathrm{MB}} + c\overrightarrow{\mathrm{MC}} \quad \cdots\cdots \text{②} \]
花子さんと太郎さんは、(1)の考察から、$\mathrm{P}$ の位置について話している。
- ① は $a=1, b=2, c=-1$ の場合だね。(1)で考えた二つの場合では、$\mathrm{M}$ の位置によって $\mathrm{P}$ の位置が異なるね。
- でも、$a=1, b=0, c=0$ の場合だと、
② は $\overrightarrow{\mathrm{MP}} = \overrightarrow{\mathrm{MA}}$ となるから、$\mathrm{M}$ がどの位置にあっても、$\mathrm{P}$ は $\mathrm{A}$ と一致するよ。- $\mathrm{P}$ の位置が変わらないのは、どのようなときかな。
ここでは
$\mathrm{M}$ がどの位置にあっても、② を満たす $\mathrm{P}$ の位置が変わらない
ための $a, b, c$ の条件を調べよう。② の両辺を、$\mathrm{A}$ を始点とするベクトルを用いて表すと、左辺は
\[ \overrightarrow{\mathrm{MP}} = \dBox{ウ} \]となり、右辺は
\begin{eqnarray} & & a\overrightarrow{\mathrm{MA}} + b\overrightarrow{\mathrm{MB}} + c\overrightarrow{\mathrm{MC}} \\[5pt] &=& \dBox{エ} \overrightarrow{\mathrm{AB}} + \dBox{オ} \overrightarrow{\mathrm{AC}} + \dBox{カ} \overrightarrow{\mathrm{AM}} \end{eqnarray}となる。したがって、② は \[ \overrightarrow{\mathrm{AP}} = \dBox{キ} \overrightarrow{\mathrm{AB}} + \dBox{ク} \overrightarrow{\mathrm{AC}} + \dBox{ケ} \overrightarrow{\mathrm{AM}} \]と変形できる。
よって、$\mathrm{M}$ がどの位置にあっても、② を満たす $\mathrm{P}$ の位置が変わらないための必要十分条件は $\dBox{コ}$ である。$\dbox{ウ}$ の解答群
0: $\overrightarrow{\mathrm{AP}} + \overrightarrow{\mathrm{AM}}$
1: $-\overrightarrow{\mathrm{AP}} + \overrightarrow{\mathrm{AM}}$
2: $\overrightarrow{\mathrm{AP}} - \overrightarrow{\mathrm{AM}}$
3: $-\overrightarrow{\mathrm{AP}} - \overrightarrow{\mathrm{AM}}$$\dbox{エ}$ ~ $\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $a$
1: $b$
2: $c$
3: $(a+b+c)$
4: $(-a+b+c)$
5: $(a-b+c)$
6: $(a+b-c)$
7: $(-a-b-c)$
8: $(1+a+b+c)$
9: $(1-a-b-c)$$\dbox{コ}$ の解答群
0: $a=b$
1: $b=c$
2: $c=a$
3: $a+b-c=0$
4: $a-b+c=1$
5: $-a+b+c=-1$
6: $a+b+c=0$
7: $a+b+c=1$
8: $a+b+c=-1$(3) $a, b, c$ を、$\dbox{コ}$ を満たす実数とする。様々な条件のもとで、② を満たす点 $\mathrm{P}$ が存在する範囲を調べよう。
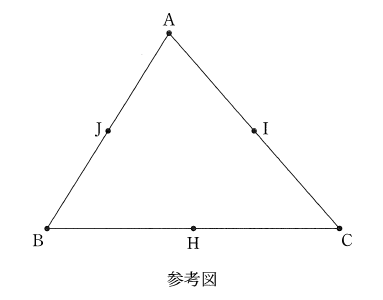
(i) $a, b, c$ が、$\dbox{コ}$ と $a = \dfrac{1}{2}$ を満たすとき、$\mathrm{P}$ が存在する範囲は $\dBox{サ}$ である。ただし、$\triangle \mathrm{ABC}$ の辺 $\mathrm{BC}$ の中点を $\mathrm{H}$、辺 $\mathrm{CA}$ の中点を $\mathrm{I}$、辺 $\mathrm{AB}$ の中点を $\mathrm{J}$ とする。
$\dbox{サ}$ の解答群
0: 直線 $\mathrm{AH}$
1: 直線 $\mathrm{BI}$
2: 直線 $\mathrm{CJ}$
3: 直線 $\mathrm{HI}$
4: 直線 $\mathrm{IJ}$
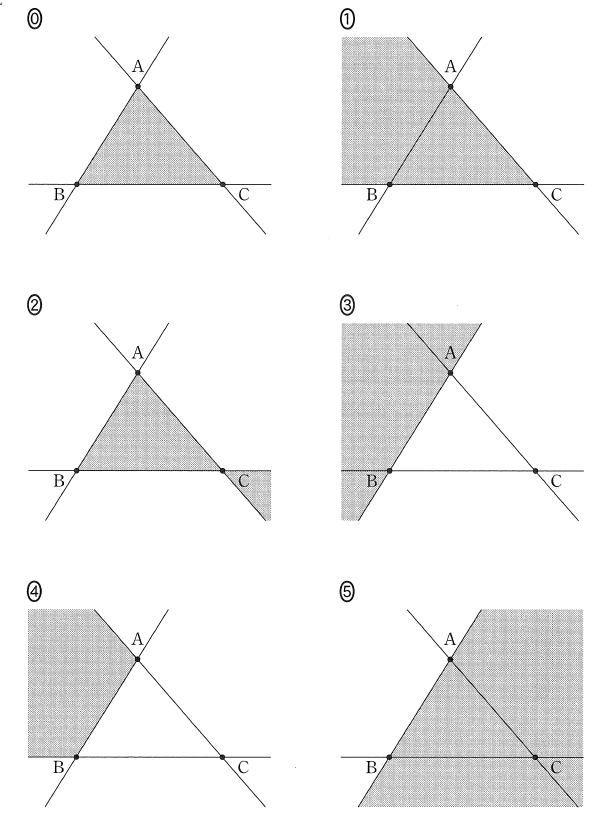
5: 直線 $\mathrm{JH}$(ii) $a, b, c$ が、$\dbox{コ}$ と $c \lt 0$ を満たすとき、$\mathrm{P}$ が存在する範囲を図示すると、$\dBox{シ}$ の灰色部分となる。ただし、境界線を含まない。
$\dbox{シ}$ については、最も適当なものを、次の0~5のうちから一つ選べ。
考え方
ベクトルの問題で内積の話が全く出てこず、点の存在範囲の話だけの問題というのは珍しいです。ただ、式変形はそんなに大変ではありません。最後の問題も、答えを選ぶだけであれば、特殊ケースを使って答えることもできるでしょう。
【第4問~第7問から3問選択】
解答編
問題
平面上に、$\triangle \mathrm{ABC}$ と点 $\mathrm{M}$ がある。
(1) 次の等式を満たす点 $\mathrm{P}$ を考える。
\[ \overrightarrow{\mathrm{MP}} = \overrightarrow{\mathrm{MA}} + 2\overrightarrow{\mathrm{MB}} - \overrightarrow{\mathrm{MC}} \quad \cdots\cdots \text{①} \]3点 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ を図1の位置にとる。ただし、図1における $\triangle \mathrm{ABC}$ は正三角形、六角形 $\mathrm{DEFGCA}$ は正六角形である。
・$\mathrm{M}$ が $\mathrm{A}$ と一致するとき、$\mathrm{P}$ は $\dBox{ア}$ と一致する。
・$\mathrm{M}$ が $\mathrm{D}$ と一致するとき、$\mathrm{P}$ は $\dBox{イ}$ と一致する。
$\dbox{ア}$ 、$\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\mathrm{A}$
1: $\mathrm{B}$
2: $\mathrm{C}$
3: $\mathrm{D}$
4: $\mathrm{E}$
5: $\mathrm{F}$
6: $\mathrm{G}$
解説
(1)
\[ \overrightarrow{\mathrm{MP}} = \overrightarrow{\mathrm{MA}} + 2\overrightarrow{\mathrm{MB}} - \overrightarrow{\mathrm{MC}} \]で、 $\mathrm{M}$ が $\mathrm{A}$ と一致するとき、
\begin{eqnarray}
\overrightarrow{\mathrm{AP}} &=& \overrightarrow{\mathrm{AA}} + 2\overrightarrow{\mathrm{AB}} - \overrightarrow{\mathrm{AC}} \\[5pt]
\overrightarrow{\mathrm{AP}} &=& 2\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{CA}} \\[5pt]
\end{eqnarray}となります。 $2\overrightarrow{\mathrm{AB}}$ は $\overrightarrow{\mathrm{AF}}$ と等しく、 $\overrightarrow{\mathrm{CA}}$ は $\overrightarrow{\mathrm{FE}}$ と等しいので、
\begin{eqnarray}
\overrightarrow{\mathrm{AP}} &=& \overrightarrow{\mathrm{AF}} + \overrightarrow{\mathrm{FE}}=\overrightarrow{\mathrm{AE}} \\[5pt]
\end{eqnarray}なので、 $\mathrm{P}$ は $\mathrm{E}$ と一致します。
また、 $\mathrm{M}$ が $\mathrm{D}$ と一致するとき、
\begin{eqnarray}
\overrightarrow{\mathrm{DP}} &=& \overrightarrow{\mathrm{DA}} + 2\overrightarrow{\mathrm{DB}} - \overrightarrow{\mathrm{DC}} \\[5pt]
\overrightarrow{\mathrm{DP}} &=& \overrightarrow{\mathrm{DA}} + 2\overrightarrow{\mathrm{DB}} + \overrightarrow{\mathrm{CD}} \\[5pt]
\overrightarrow{\mathrm{DP}} &=& \overrightarrow{\mathrm{CA}} + 2\overrightarrow{\mathrm{DB}} \\[5pt]
\overrightarrow{\mathrm{DP}} &=& \overrightarrow{\mathrm{BD}} + 2\overrightarrow{\mathrm{DB}} \\[5pt]
\overrightarrow{\mathrm{DP}} &=& \overrightarrow{\mathrm{DB}} \\[5pt]
\end{eqnarray}なので、 $\mathrm{P}$ は $\mathrm{B}$ と一致します。
解答
ア:4 (2点)
イ:1 (2点)
解答編 つづき
問題
(2) $a, b, c$ を実数とする。次の等式を満たす点 $\mathrm{P}$ を考える。
\[ \overrightarrow{\mathrm{MP}} = a\overrightarrow{\mathrm{MA}} + b\overrightarrow{\mathrm{MB}} + c\overrightarrow{\mathrm{MC}} \quad \cdots\cdots \text{②} \]
花子さんと太郎さんは、(1)の考察から、$\mathrm{P}$ の位置について話している。
- ① は $a=1, b=2, c=-1$ の場合だね。(1)で考えた二つの場合では、$\mathrm{M}$ の位置によって $\mathrm{P}$ の位置が異なるね。
- でも、$a=1, b=0, c=0$ の場合だと、
② は $\overrightarrow{\mathrm{MP}} = \overrightarrow{\mathrm{MA}}$ となるから、$\mathrm{M}$ がどの位置にあっても、$\mathrm{P}$ は $\mathrm{A}$ と一致するよ。- $\mathrm{P}$ の位置が変わらないのは、どのようなときかな。
ここでは
$\mathrm{M}$ がどの位置にあっても、② を満たす $\mathrm{P}$ の位置が変わらない
ための $a, b, c$ の条件を調べよう。② の両辺を、$\mathrm{A}$ を始点とするベクトルを用いて表すと、左辺は
\[ \overrightarrow{\mathrm{MP}} = \dBox{ウ} \]となり、右辺は
\begin{eqnarray} & & a\overrightarrow{\mathrm{MA}} + b\overrightarrow{\mathrm{MB}} + c\overrightarrow{\mathrm{MC}} \\[5pt] &=& \dBox{エ} \overrightarrow{\mathrm{AB}} + \dBox{オ} \overrightarrow{\mathrm{AC}} + \dBox{カ} \overrightarrow{\mathrm{AM}} \end{eqnarray}となる。したがって、② は \[ \overrightarrow{\mathrm{AP}} = \dBox{キ} \overrightarrow{\mathrm{AB}} + \dBox{ク} \overrightarrow{\mathrm{AC}} + \dBox{ケ} \overrightarrow{\mathrm{AM}} \]と変形できる。
よって、$\mathrm{M}$ がどの位置にあっても、② を満たす $\mathrm{P}$ の位置が変わらないための必要十分条件は $\dBox{コ}$ である。$\dbox{ウ}$ の解答群
0: $\overrightarrow{\mathrm{AP}} + \overrightarrow{\mathrm{AM}}$
1: $-\overrightarrow{\mathrm{AP}} + \overrightarrow{\mathrm{AM}}$
2: $\overrightarrow{\mathrm{AP}} - \overrightarrow{\mathrm{AM}}$
3: $-\overrightarrow{\mathrm{AP}} - \overrightarrow{\mathrm{AM}}$$\dbox{エ}$ ~ $\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $a$
1: $b$
2: $c$
3: $(a+b+c)$
4: $(-a+b+c)$
5: $(a-b+c)$
6: $(a+b-c)$
7: $(-a-b-c)$
8: $(1+a+b+c)$
9: $(1-a-b-c)$$\dbox{コ}$ の解答群
0: $a=b$
1: $b=c$
2: $c=a$
3: $a+b-c=0$
4: $a-b+c=1$
5: $-a+b+c=-1$
6: $a+b+c=0$
7: $a+b+c=1$
8: $a+b+c=-1$
解説
(2)
\begin{eqnarray}
\overrightarrow{\mathrm{MP}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{AP}}-\overrightarrow{\mathrm{AM}}
\end{eqnarray}が成り立ちます。
また、
\begin{eqnarray}
& &
a\overrightarrow{\mathrm{MA}} + b\overrightarrow{\mathrm{MB}} + c\overrightarrow{\mathrm{MC}} \\[5pt]
&=&
-a\overrightarrow{\mathrm{AM}} + b\left(\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AM}}\right) + c\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AM}}\right) \\[5pt]
&=&
b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}} +(-a-b-c)\overrightarrow{\mathrm{AM}} \\[5pt]
\end{eqnarray}と変形できます。
なので、② は
\begin{eqnarray}
\overrightarrow{\mathrm{AP}}-\overrightarrow{\mathrm{AM}}
&=&
b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}} +(-a-b-c)\overrightarrow{\mathrm{AM}} \\[5pt]
\overrightarrow{\mathrm{AP}}
&=&
b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}} +(1-a-b-c)\overrightarrow{\mathrm{AM}} \\[5pt]
\end{eqnarray}と変形できます。
$\mathrm{M}$ がどの位置にあっても、② を満たす $\mathrm{P}$ の位置が変わらない、ということは、上の式で $\overrightarrow{\mathrm{AM}}$ の影響がないときなので、係数が $0$ 、つまり、 $a+b+c=1$ と同値であることがわかります。
解答
ウ:2 (1点)
エオカ:127 (2点)
キクケ:129 (2点)
コ:7 (2点)
解答編 つづき
問題
(3) $a, b, c$ を、$\dbox{コ}$ を満たす実数とする。様々な条件のもとで、② を満たす点 $\mathrm{P}$ が存在する範囲を調べよう。
(i) $a, b, c$ が、$\dbox{コ}$ と $a = \dfrac{1}{2}$ を満たすとき、$\mathrm{P}$ が存在する範囲は $\dBox{サ}$ である。ただし、$\triangle \mathrm{ABC}$ の辺 $\mathrm{BC}$ の中点を $\mathrm{H}$、辺 $\mathrm{CA}$ の中点を $\mathrm{I}$、辺 $\mathrm{AB}$ の中点を $\mathrm{J}$ とする。
$\dbox{サ}$ の解答群
0: 直線 $\mathrm{AH}$
1: 直線 $\mathrm{BI}$
2: 直線 $\mathrm{CJ}$
3: 直線 $\mathrm{HI}$
4: 直線 $\mathrm{IJ}$
5: 直線 $\mathrm{JH}$
解説
(3)(i)
$a+b+c=1$ を満たすので、\[ \overrightarrow{\mathrm{AP}} = b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}} \]が、成り立つことを使って考えていきます。
$a=\dfrac{1}{2}$ なので、 $b+c=\dfrac{1}{2}$ となります。上の式を変形すると
\begin{eqnarray}
\overrightarrow{\mathrm{AP}}
&=&
b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}} \\[5pt]
&=&
2b \cdot \frac{1}{2}\overrightarrow{\mathrm{AB}} + 2c \cdot \frac{1}{2} \overrightarrow{\mathrm{AC}} \\[5pt]
&=&
2b \overrightarrow{\mathrm{AJ}} + 2c \overrightarrow{\mathrm{AI}} \\[5pt]
\end{eqnarray}となります。このとき、係数の和は $2b+2c=1$ なので、この条件を満たしながら $b,c$ が動くと、 $\mathrm{P}$ は直線 $\mathrm{IJ}$ 上に存在することがわかります。
解答
サ:4 (2点)
解答編 つづき
問題
(ii) $a, b, c$ が、$\dbox{コ}$ と $c \lt 0$ を満たすとき、$\mathrm{P}$ が存在する範囲を図示すると、$\dBox{シ}$ の灰色部分となる。ただし、境界線を含まない。
$\dbox{シ}$ については、最も適当なものを、次の0~5のうちから一つ選べ。
解説
(3)(ii)
(3)(i)を使って考えます。 $a=\dfrac{1}{2}$ のとき、 $\mathrm{P}$ は直線 $\mathrm{IJ}$ 上にあります。さらに、 $b,c$ がともに正のときには、線分 $\mathrm{IJ}$ 上にあります。 $c=0$ のときには $\mathrm{P}$ は $\mathrm{J}$ にいるのだから、 $c\lt 0$ のときには、問題文にある図で言うと、直線 $\mathrm{IJ}$ のうち、 $\mathrm{J}$ より左の部分に存在することになります。なので、その部分は少なくとも答えに含まれていないといけないので、選択肢の中では 1, 3, 4 が該当します。また、三角形の内部は入らないので、3 か 4 だとわかります。
$a,b$ はとりうる値の範囲に制限がないので、例えば $a\lt 0$ とすると、 $b\gt 1$ となります。このとき、 $b \overrightarrow{\mathrm{AB}}$ は、大きさが $\mathrm{AB}$ の長さより大きくなるため、 $\overrightarrow{\mathrm{AP}}=b\overrightarrow{\mathrm{AB}} + c\overrightarrow{\mathrm{AC}}$ を満たす $\mathrm{P}$ は、図の $\mathrm{B}$ より下にも行くことができます。なので、選択肢 3 が答えだと絞られます。
答えを絞るだけであればこれで十分ですが、選択肢がなかった場合にどうやって解くかも考えてみましょう。
$c$ にだけ条件がついているので、逆に $c$ を消して考えたほうがわかりやすいです。 $a+b+c=1$ であることを使うと
\begin{eqnarray}
\overrightarrow{\mathrm{AP}} &=& b \overrightarrow{\mathrm{AB}} + c \overrightarrow{\mathrm{AC}} \\[5pt]
\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AP}} &=& (a+b+c) \overrightarrow{\mathrm{CA}} + b \overrightarrow{\mathrm{AB}} + c \overrightarrow{\mathrm{AC}} \\[5pt]
\overrightarrow{\mathrm{CP}} &=& a\overrightarrow{\mathrm{CA}} + b \overrightarrow{\mathrm{CB}} \\[5pt]
\end{eqnarray}となります。ここで、 $a+b=1-c$ なので、 $c\lt 0$ のとき、 $a+b\gt 1$ となります。
上の式をさらにこのように変形します。
\begin{eqnarray}
\overrightarrow{\mathrm{CP}}
&=&
a\overrightarrow{\mathrm{CA}} + b \overrightarrow{\mathrm{CB}} \\[5pt]
&=&
\frac{a}{1-c} \cdot (1-c)\overrightarrow{\mathrm{CA}} + \frac{b}{1-c} \cdot (1-c) \overrightarrow{\mathrm{CB}} \\[5pt]
\end{eqnarray}ここで、 $\overrightarrow{\mathrm{CX}}=(1-c)\overrightarrow{\mathrm{CA}}$, $\overrightarrow{\mathrm{CY}}=(1-c)\overrightarrow{\mathrm{CB}}$ となるように $\mathrm{X,Y}$ をとったとします。 $1-c\gt 1$ より、 $\mathrm{X}$ は直線 $\mathrm{AC}$ の $\mathrm{A}$ 側の延長線上にあり、 $\mathrm{Y}$ は直線 $\mathrm{BC}$ の $\mathrm{B}$ 側の延長線上にあり、直線 $\mathrm{XY}$ は直線 $\mathrm{AB}$ と平行です。また、\[ \frac{a}{1-c} \overrightarrow{\mathrm{CX}} + \frac{b}{1-c} \overrightarrow{\mathrm{CY}} \]とかけて、係数の和は $1$ なので、 $c$ をとめて $a,b$ を自由に動かすと、点 $\mathrm{P}$ は直線 $\mathrm{XY}$ 上を動きます。さらに $c$ を $c\lt 0$ の範囲で動かすと、この直線が、直線 $\mathrm{AB}$ から見て $\mathrm{C}$ を含まない側全体を動くので、点 $\mathrm{P}$ の動く範囲は選択肢 3 の通りだとわかります。
解答
シ:3 (3点)