共通テスト 数学II・数学B・数学C 2026年度 第3問 解説
【必答問題】
問題編
問題
(1) $k$ を実数とし、3次関数 $f(x) = \dfrac{1}{3}x^3 - 2x^2 + 3x + k$ を考える。
(i) $f'(x) = \dBox{ア}$ である。
$x = \myBox{イ}$ のとき、$f(x)$ は極大値 $\dBox{ウ}$ をとる。
$x = \myBox{エ}$ のとき、$f(x)$ は極小値 $\dBox{オ}$ をとる。$\dbox{ア}$ の解答群
0: $\dfrac{1}{3}x^2 - 2x + 3$
1: $\dfrac{1}{3}x^2 - 2x + 3 + k$
2: $x^2 - 4x + 3$
3: $x^2 - 4x + 3 + k$
4: $\dfrac{1}{12}x^4 - \dfrac{2}{3}x^3 + \dfrac{3}{2}x^2 +
kx$5: $\dfrac{1}{3}x^4 - 2x^3 + 3x^2 + kx$
$\dbox{ウ}$ 、$\dbox{オ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $2$
3: $\dfrac{2}{3}$
4: $\dfrac{4}{3}$
5: $k$
6: $-\dfrac{4}{3} + k$
7: $-\dfrac{2}{3} + k$
8: $\dfrac{2}{3} + k$
9: $\dfrac{4}{3} + k$
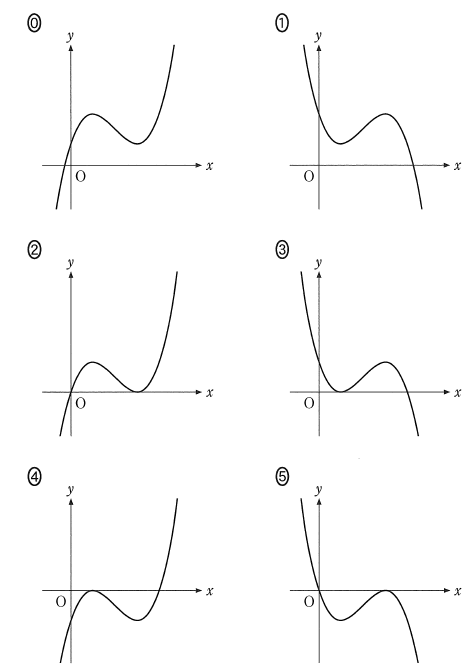
(ii) $y=f(x)$ のグラフの概形は
$k=0$ のとき $\dBox{カ}$
$k \gt 0$ のとき $\dBox{キ}$
である。$\dbox{カ}$ 、$\dbox{キ}$ については、最も適当なものを、次の0~5のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(iii) (i) で求めた $\mybox{イ}$ 、$\mybox{エ}$ のうち、小さい方の数を $\alpha$ とする。 $f(0) \lt 0 \lt f(\alpha)$ を満たすような $k$ の値の範囲は $\dBox{ク} \lt k \lt \dBox{ケ}$ である。
$k$ は $\mybox{ク} \lt k \lt \mybox{ケ}$ を満たすとする。$0 \leqq x \leqq \alpha$ の範囲において、 $f(x) = 0$ を満たす $x$ の値を $\beta$ とおく。$0 \leqq x \leqq \beta$ の範囲における $y = f(x)$ のグラフと $x$ 軸および $y$ 軸で囲まれた部分の面積と、$\beta \leqq x \leqq \alpha$ の範囲における $y = f(x)$ のグラフと $x$ 軸および直線 $x = \alpha$ で囲まれた部分の面積が等しいとする。
このとき、$\dBox{コ}$ が成り立つ。したがって、$k = \dfrac{\myBox{サシス}}{\myBox{セソ}}$ である。
$\mybox{ク}$ 、$\mybox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $\dfrac{2}{3}$
2: $\dfrac{3}{4}$
3: $\dfrac{4}{3}$
4: $\dfrac{3}{2}$
5: $-\dfrac{5}{2}$
6: $-\dfrac{2}{3}$
7: $-\dfrac{3}{4}$
8: $-\dfrac{4}{3}$
9: $-\dfrac{3}{2}$
$\dbox{コ}$ の解答群
0: $\displaystyle \int_0^\beta f(x) \,dx = \int_\beta^\alpha f(x) \,dx$
1: $\displaystyle \int_0^\alpha f(x) \,dx = 0$
2: $\displaystyle \int_0^\beta f(x) \,dx = 0$
3: $\displaystyle \int_\beta^\alpha f(x) \,dx = 0$
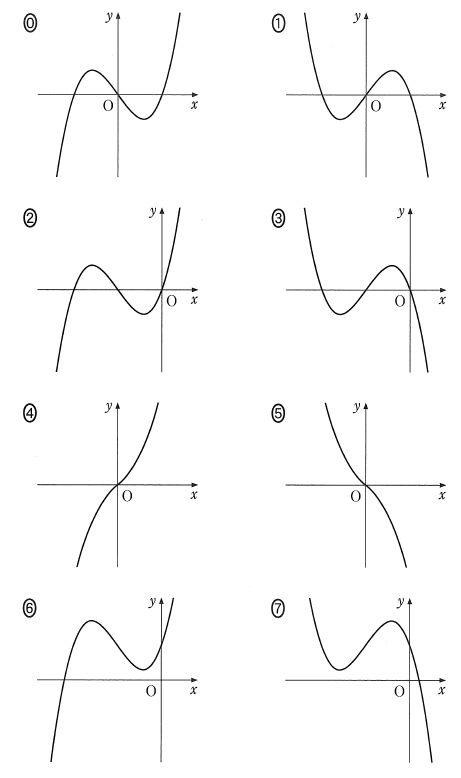
(2) 3次関数 $g(x)$ に対して、与えられた条件のもとで $y=g(x)$ のグラフの概形を考えよう。
・次の条件(a)を考える。
条件(a) $g(0) = 0$ かつ $g'(0) \gt 0$ である。
後の0~7のうち、条件(a)を満たす関数 $y=g(x)$ のグラフの概形は
$\dBox{タ}$ 、$\dBox{チ}$ 、$\dBox{ツ}$ の三つであり、残りの五つは条件(a)を満たさない。ただし、$\dbox{タ}$ 、$\dbox{チ}$ 、$\dbox{ツ}$ の解答の順序は問わない。・条件(a)に加えて、次の条件(b)を考える。
条件(b) $y=g'(x)$ のグラフは直線 $x=0$ を軸とする放物線である。
後の0~7のうち、条件(a)、(b)をともに満たす関数 $y=g(x)$ のグラフの概形は $\dBox{テ}$ 、$\dBox{ト}$ の二つであり、残りの六つは条件(a)、(b)の少なくとも一方を満たさない。ただし、$\dbox{テ}$ 、$\dbox{ト}$ の解答の順序は問わない。
・条件(a)、(b)に加えて、次の条件(c)を考える。
条件(c) $y=g'(x)$ のグラフは下に凸の放物線である。
後の0~7のうち、条件(a)、(b)、(c)のすべてを満たす関数 $y=g(x)$ のグラフの概形は $\dBox{ナ}$ の一つだけである。
$\dbox{タ}$ ~ $\dbox{ナ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
考え方
(1)と(2)は独立している問題です。(1)(iii)は面積の話を積分で表しましょう。
(2)は、普段は微分をして増減表を書いてからグラフをかく、という流れですが、それを逆順にした問題です。グラフを見て、増減表や微分がどうなっているかを考えます。条件を増やして候補を絞っていくので、途中でミスるとその先もミスになる可能性が高いので注意しましょう。
【必答問題】
解答編
問題
(1) $k$ を実数とし、3次関数 $f(x) = \dfrac{1}{3}x^3 - 2x^2 + 3x + k$ を考える。
(i) $f'(x) = \dBox{ア}$ である。
$x = \myBox{イ}$ のとき、$f(x)$ は極大値 $\dBox{ウ}$ をとる。
$x = \myBox{エ}$ のとき、$f(x)$ は極小値 $\dBox{オ}$ をとる。$\dbox{ア}$ の解答群
0: $\dfrac{1}{3}x^2 - 2x + 3$
1: $\dfrac{1}{3}x^2 - 2x + 3 + k$
2: $x^2 - 4x + 3$
3: $x^2 - 4x + 3 + k$
4: $\dfrac{1}{12}x^4 - \dfrac{2}{3}x^3 + \dfrac{3}{2}x^2 +
kx$5: $\dfrac{1}{3}x^4 - 2x^3 + 3x^2 + kx$
$\dbox{ウ}$ 、$\dbox{オ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $2$
3: $\dfrac{2}{3}$
4: $\dfrac{4}{3}$
5: $k$
6: $-\dfrac{4}{3} + k$
7: $-\dfrac{2}{3} + k$
8: $\dfrac{2}{3} + k$
9: $\dfrac{4}{3} + k$
解説
(1)(i)
$f(x) = \dfrac{1}{3}x^3 - 2x^2 + 3x + k$ なので、
\begin{eqnarray}
f'(x) &=& x^2-4x+3
\end{eqnarray}となります。さらに変形すると\[ f'(x)=(x-1)(x-3) \]となるので、増減表は以下のようになります。
\begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 3 & \cdots \\
\hline
f'(x) & + & 0 & - & 0 & + \\
\hline
f(x) & \nearrow & & \searrow & & \nearrow &
\end{array}
よって、 $x=1$ のときに極大値
\begin{eqnarray}
\frac{1}{3}-2+3+k=\frac{4}{3}+k
\end{eqnarray}をとり、 $x=3$ のときに極小値
\begin{eqnarray}
\frac{3^3}{3}-2\cdot 9+3\cdot 3+k=k
\end{eqnarray}をとることがわかります。
解答
ア:2 (2点)
イウ:19 (2点)
エオ:35 (2点)
解答編 つづき
問題
(ii) $y=f(x)$ のグラフの概形は
$k=0$ のとき $\dBox{カ}$
$k \gt 0$ のとき $\dBox{キ}$
である。$\dbox{カ}$ 、$\dbox{キ}$ については、最も適当なものを、次の0~5のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
解説
(1)(ii)
$x=1$ で極大値をとり、 $x=3$ で極小値をとることから、少なくともグラフは、選択肢 0, 2, 4 のどれかです。
$f(0)=k$ なので、 $x=0$ のときの $y$ 座標で判断すればいいです。 $k=0$ のときのグラフは、原点を通っている選択肢2だとわかります。 $k\gt 0$ のときのグラフは、 $y$ 軸とは原点より上のところで交わっているはずなので、選択肢0だとわかります。
解答
カ:2 (2点)
キ:0 (2点)
解答編 つづき
問題
(iii) (i) で求めた $\mybox{イ}$ 、$\mybox{エ}$ のうち、小さい方の数を $\alpha$ とする。 $f(0) \lt 0 \lt f(\alpha)$ を満たすような $k$ の値の範囲は $\dBox{ク} \lt k \lt \dBox{ケ}$ である。
$k$ は $\mybox{ク} \lt k \lt \mybox{ケ}$ を満たすとする。$0 \leqq x \leqq \alpha$ の範囲において、 $f(x) = 0$ を満たす $x$ の値を $\beta$ とおく。$0 \leqq x \leqq \beta$ の範囲における $y = f(x)$ のグラフと $x$ 軸および $y$ 軸で囲まれた部分の面積と、$\beta \leqq x \leqq \alpha$ の範囲における $y = f(x)$ のグラフと $x$ 軸および直線 $x = \alpha$ で囲まれた部分の面積が等しいとする。
このとき、$\dBox{コ}$ が成り立つ。したがって、$k = \dfrac{\myBox{サシス}}{\myBox{セソ}}$ である。
$\mybox{ク}$ 、$\mybox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $\dfrac{2}{3}$
2: $\dfrac{3}{4}$
3: $\dfrac{4}{3}$
4: $\dfrac{3}{2}$
5: $-\dfrac{5}{2}$
6: $-\dfrac{2}{3}$
7: $-\dfrac{3}{4}$
8: $-\dfrac{4}{3}$
9: $-\dfrac{3}{2}$
$\dbox{コ}$ の解答群
0: $\displaystyle \int_0^\beta f(x) \,dx = \int_\beta^\alpha f(x) \,dx$
1: $\displaystyle \int_0^\alpha f(x) \,dx = 0$
2: $\displaystyle \int_0^\beta f(x) \,dx = 0$
3: $\displaystyle \int_\beta^\alpha f(x) \,dx = 0$
解説
(1)(iii)
(1)(i)の計算より、 $\alpha=1$ です。
$f(0)=k$ であり、 $f(\alpha)=f(1)=\dfrac{4}{3}+k$ です。なので、 $f(0) \lt 0\lt f(\alpha)$ を満たす範囲とは、\[ k\lt 0 \lt \dfrac{4}{3}+k \]を満たす範囲です。左の不等式から\[ k\lt 0 \]が得られ、右の不等式から\[ k\gt -\dfrac{4}{3} \]なので、 $k$ の範囲は\[ -\dfrac{4}{3} \lt k \lt 0 \]となります。
$x\lt \alpha$ の範囲では $f(x)$ は単調増加なので、 $0\leqq x\leqq \beta$ では $y=f(x)$ のグラフは $x$ 軸より下にあるので、「$0 \leqq x \leqq \beta$ の範囲における $y = f(x)$ のグラフと $x$ 軸および $y$ 軸で囲まれた部分の面積」は\[ -\int_0^\beta f(x) \,dx \]と表すことができます。
$\beta\leqq x\leqq \alpha$ では $y=f(x)$ のグラフは $x$ 軸より上にあるので、「$\beta \leqq x \leqq \alpha$ の範囲における $y = f(x)$ のグラフと $x$ 軸および直線 $x = \alpha$ で囲まれた部分の面積」は\[ \int_\beta^\alpha f(x) \,dx \]と表すことができます。
両者が等しいということは
\begin{eqnarray}
-\int_0^\beta f(x) \,dx &=& \int_\beta^\alpha f(x) \,dx \\[5pt]
\int_0^\beta f(x) \,dx +\int_\beta^\alpha f(x) \,dx=0 \\[5pt]
\int_0^\alpha f(x) \,dx=0 \\[5pt]
\end{eqnarray}が成り立つということです。
左辺を計算すると
\begin{eqnarray}
& &
\int_0^1 \left(\dfrac{1}{3}x^3 - 2x^2 + 3x + k \right) dx \\[5pt]
&=&
\left[\dfrac{1}{12}x^4 - \frac{2}{3}x^3 + \frac{3}{2}x^2 + kx \right]_0^1 \\[5pt]
&=&
\dfrac{1}{12} - \frac{2}{3} + \frac{3}{2} + k \\[5pt]
&=&
\frac{1-8+18}{12} + k \\[5pt]
&=&
\frac{11}{12} + k \\[5pt]
\end{eqnarray}なので、これが $0$ となることから $k=-\dfrac{11}{12}$ だとわかります。
解答
クケ:80 (2点)
コ:1 (2点)
サシスセ:-1112 (2点)
解答編 つづき
問題
(2) 3次関数 $g(x)$ に対して、与えられた条件のもとで $y=g(x)$ のグラフの概形を考えよう。
・次の条件(a)を考える。
条件(a) $g(0) = 0$ かつ $g'(0) \gt 0$ である。
後の0~7のうち、条件(a)を満たす関数 $y=g(x)$ のグラフの概形は
$\dBox{タ}$ 、$\dBox{チ}$ 、$\dBox{ツ}$ の三つであり、残りの五つは条件(a)を満たさない。ただし、$\dbox{タ}$ 、$\dbox{チ}$ 、$\dbox{ツ}$ の解答の順序は問わない。・条件(a)に加えて、次の条件(b)を考える。
条件(b) $y=g'(x)$ のグラフは直線 $x=0$ を軸とする放物線である。
後の0~7のうち、条件(a)、(b)をともに満たす関数 $y=g(x)$ のグラフの概形は $\dBox{テ}$ 、$\dBox{ト}$ の二つであり、残りの六つは条件(a)、(b)の少なくとも一方を満たさない。ただし、$\dbox{テ}$ 、$\dbox{ト}$ の解答の順序は問わない。
・条件(a)、(b)に加えて、次の条件(c)を考える。
条件(c) $y=g'(x)$ のグラフは下に凸の放物線である。
後の0~7のうち、条件(a)、(b)、(c)のすべてを満たす関数 $y=g(x)$ のグラフの概形は $\dBox{ナ}$ の一つだけである。
$\dbox{タ}$ ~ $\dbox{ナ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
解説
(2)
条件(a) 「$g(0) = 0$ かつ $g'(0) \gt 0$」を考えます。これは、原点を通ること、原点での接線の傾きが正であることを表しています。
なので、「原点を通る」という条件から、6と7が除外されます。
「原点での接線の傾きが正である」という条件から、さらに、0, 3, 5 が除外されます。
残った、1, 2, 4 は条件を満たします。
さらに、条件(b)「$y=g'(x)$ のグラフは直線 $x=0$ を軸とする放物線である。」を考えます。
$x=0$ を軸とする放物線、ということは、 $0$ でない定数 $a$ を使って、 $g'(x)=ax^2+c$ と書けることを表しています。 $g'(0)\gt 0$ という条件から、 $c\gt 0$ です。
もし、 $a\gt 0$ なら下に凸の放物線です。 $c\gt 0$ なので、 $g'(x)$ はつねに正だから、選択肢4のように、ずっと増加し続けます。
もし、 $a\lt 0$ なら上に凸の放物線です。 $c\gt 0$ なので、 $g'(x)$ の値は、負、正、負、と変化していきます。なので、選択肢1のように、減る・増える・減る、となっているはずです。
選択肢2だと、$y$ 軸より左のところで極値をとっているので、 $g'(x)=0$ の解が2つの負の実数となってしまいます。なので、 $g'(x)=ax^2+c$ とはかけません。
以上から、条件(a)(b)両方満たすものは、選択肢1と4のみです。
最後に追加された条件(c)「$y=g'(x)$ のグラフは下に凸の放物線である。」については、先ほど述べたように、選択肢4のようになっていることがわかります。
解答
タ・チ・ツ:1・2・4 (2点)
テ・ト:1・4 (2点)
ナ:4 (2点)