共通テスト 数学II・数学B・数学C 2026年度 第2問 解説
【必答問題】
問題編
問題
(1) 二つの角 $A, B$ に対し
\[ \sin A + \sin B = 2 \sin \dfrac{A+B}{2} \cos \dfrac{A-B}{2} \quad \cdots \text{①} \]が成り立つことを示そう。二つの角 $\alpha, \beta$ に対し、加法定理から
\begin{eqnarray} \sin (\alpha + \beta) = \dBox{ア} + \cos \alpha \sin \beta \quad \cdots \text{②} \\[5pt] \sin (\alpha - \beta) = \dbox{ア} - \cos \alpha \sin \beta \quad \cdots \text{③} \end{eqnarray}である。② と ③ の左辺どうし、右辺どうしを加え、$\alpha = \dBox{イ}, \beta = \dBox{ウ}$ とすると、① が得られる。$\dbox{ア}$ の解答群
0: $\sin \alpha \sin \beta$
1: $\sin \alpha \cos \beta$
2: $\cos \alpha \sin \beta$
3: $\cos \alpha \cos \beta$
4: $\sin^2 \alpha$
5: $\sin^2 \beta$
6: $\cos^2 \alpha$
7: $\cos^2 \beta$$\dbox{イ}, \dbox{ウ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $A$
1: $B$
2: $A+B$
3: $A-B$4: $\dfrac{A+B}{2}$
5: $\dfrac{A-B}{2}$
6: $\dfrac{A+B}{4}$
7: $\dfrac{A-B}{4}$
(2) 関数 $f(x)$ を
\[ f(x) = \sin \left( x + \dfrac{5}{12}\pi \right) + \sin \left( x + \dfrac{\pi}{12} \right) \]とする。
$0 \leqq x \lt 2\pi$ の範囲で $f(x)$ の最大値を考えよう。
① を用いると
\begin{eqnarray} f(x) &=& 2 \sin \left( x + \dBox{エ} \right) \cos \dBox{オ} \\[5pt] &=& 2 \cos \dbox{オ} \sin \left( x + \dbox{エ} \right) \end{eqnarray}と変形できる。$2 \cos \dbox{オ}$ は正の定数であるから、$0 \leqq x \lt 2\pi$ の範囲において、$f(x)$ は $x = \dBox{カ}$ で最大値 $\dBox{キ}$ をとる。
$\dbox{エ}$ ~ $\dbox{カ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $0$
1: $\dfrac{\pi}{12}$
2: $\dfrac{\pi}{6}$
3: $\dfrac{\pi}{4}$
4: $\dfrac{\pi}{3}$
5: $\dfrac{\pi}{2}$
6: $\dfrac{3}{4}\pi$
7: $\pi$
$\dbox{キ}$ の解答群
0: $\dfrac{1}{2}$
1: $1$
2: $2$
3: $\dfrac{\sqrt{2}}{2}$
4: $\dfrac{\sqrt{3}}{2}$
5: $\sqrt{2}$
6: $\sqrt{3}$
7: $2\sqrt{2}$
(3) $a$ を $0 \lt a \lt \pi$ を満たす定数とし、関数 $g(x)$ を
\[ g(x) = \sin (x+a) + \sin (x+2a) + \sin (x+3a) \]とする。
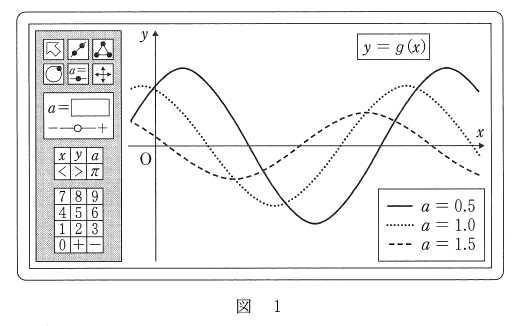
花子さんと太郎さんは、関数 $y=g(x)$ のグラフをコンピュータを用いて表示させてみた。図1は、$a=0.5, a=1.0, a=1.5$ としたときの $y=g(x)$ のグラフである。これを見て、花子さんと太郎さんは、関数 $g(x)$ について話している。
- $g(x)$ は、定数 $p, q$ を用いて $g(x) = p \sin (x+q)$ と変形できそうだね。
- 三つの関数 $\sin (x+a), \sin (x+2a), \sin (x+3a)$ のうちの二つの関数の和に ① を使うと、残り一つの関数の定数倍にできるかな。
(i) ① を用いると、関数 $\sin (x+a), \sin (x+2a), \sin (x+3a)$ のうちの二つの関数の和 $\dBox{ク}$ は、残りの関数 $\sin \left( x + \dBox{ケ} \right)$ の定数倍となる。
したがって、関数 $g(x)$ は
\[ g(x) = \dBox{コ} \sin \left( x + \dbox{ケ} \right) \]と変形することができる。$\dbox{ク}$ の解答群
0: $\sin (x+a) + \sin (x+2a)$
1: $\sin (x+a) + \sin (x+3a)$
2: $\sin (x+2a) + \sin (x+3a)$$\dbox{ケ}$ の解答群
0: $a$
1: $2a$
2: $3a$$\dbox{コ}$ の解答群
0: $2 \cos a$
1: $-2 \cos a$
2: $2 \cos 2a$
3: $-2 \cos 2a$
4: $(2 \cos a + 1)$
5: $(-2 \cos a + 1)$
6: $(2 \cos 2a + 1)$
7: $(-2 \cos 2a + 1)$(ii) $a = \dfrac{5}{6}\pi$ のとき、$0 \leqq x \lt 2\pi$ の範囲において、$g(x)$ は $x = \dfrac{\myBox{サシ}}{\myBox{ス}}\pi$ で最大値 $\dBox{セ}$ をとる。
$\dbox{セ}$ の解答群
0: $0$
1: $1$
2: $2$
3: $-1$
4: $-2$
5: $\sqrt{3}$
6: $-\sqrt{3}$
7: $\sqrt{3} + 1$
8: $\sqrt{3} - 1$
9: $-\sqrt{3} + 1$
考え方
使う式が指定されているので、それに従って解いていきます。しかも、指定されている式は教科書でも紹介されている公式なので、かなり親切です。最後まで計算間違いに注意して解きましょう。
【必答問題】
解答編
問題
(1) 二つの角 $A, B$ に対し
\[ \sin A + \sin B = 2 \sin \dfrac{A+B}{2} \cos \dfrac{A-B}{2} \quad \cdots \text{①} \]が成り立つことを示そう。二つの角 $\alpha, \beta$ に対し、加法定理から
\begin{eqnarray} \sin (\alpha + \beta) = \dBox{ア} + \cos \alpha \sin \beta \quad \cdots \text{②} \\[5pt] \sin (\alpha - \beta) = \dbox{ア} - \cos \alpha \sin \beta \quad \cdots \text{③} \end{eqnarray}である。② と ③ の左辺どうし、右辺どうしを加え、$\alpha = \dBox{イ}, \beta = \dBox{ウ}$ とすると、① が得られる。$\dbox{ア}$ の解答群
0: $\sin \alpha \sin \beta$
1: $\sin \alpha \cos \beta$
2: $\cos \alpha \sin \beta$
3: $\cos \alpha \cos \beta$
4: $\sin^2 \alpha$
5: $\sin^2 \beta$
6: $\cos^2 \alpha$
7: $\cos^2 \beta$$\dbox{イ}, \dbox{ウ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $A$
1: $B$
2: $A+B$
3: $A-B$4: $\dfrac{A+B}{2}$
5: $\dfrac{A-B}{2}$
6: $\dfrac{A+B}{4}$
7: $\dfrac{A-B}{4}$
解説
(1)
加法定理より
\begin{eqnarray}
\sin(\alpha+\beta) &=& \sin\alpha\cos\beta+\cos\alpha\sin\beta \\[5pt]
\sin(\alpha-\beta) &=& \sin\alpha\cos\beta-\cos\alpha\sin\beta \\[5pt]
\end{eqnarray}なので、辺々を加えると
\begin{eqnarray}
\sin(\alpha+\beta)+\sin(\alpha-\beta) &=& 2\sin\alpha\cos\beta
\end{eqnarray}となります。ここで、 $\alpha=\dfrac{A+B}{2}$, $\beta=\dfrac{A-B}{2}$ とすれば
\begin{eqnarray}
\sin A+\sin B &=& 2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}
\end{eqnarray}となり、①が得られます。
解答
ア:1 (1点)
イウ:45 (2点)
解答編 つづき
問題
(2) 関数 $f(x)$ を
\[ f(x) = \sin \left( x + \dfrac{5}{12}\pi \right) + \sin \left( x + \dfrac{\pi}{12} \right) \]とする。
$0 \leqq x \lt 2\pi$ の範囲で $f(x)$ の最大値を考えよう。
① を用いると
\begin{eqnarray} f(x) &=& 2 \sin \left( x + \dBox{エ} \right) \cos \dBox{オ} \\[5pt] &=& 2 \cos \dbox{オ} \sin \left( x + \dbox{エ} \right) \end{eqnarray}と変形できる。$2 \cos \dbox{オ}$ は正の定数であるから、$0 \leqq x \lt 2\pi$ の範囲において、$f(x)$ は $x = \dBox{カ}$ で最大値 $\dBox{キ}$ をとる。
$\dbox{エ}$ ~ $\dbox{カ}$ については、最も適当なものを、次の0~7のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $0$
1: $\dfrac{\pi}{12}$
2: $\dfrac{\pi}{6}$
3: $\dfrac{\pi}{4}$
4: $\dfrac{\pi}{3}$
5: $\dfrac{\pi}{2}$
6: $\dfrac{3}{4}\pi$
7: $\pi$
$\dbox{キ}$ の解答群
0: $\dfrac{1}{2}$
1: $1$
2: $2$
3: $\dfrac{\sqrt{2}}{2}$
4: $\dfrac{\sqrt{3}}{2}$
5: $\sqrt{2}$
6: $\sqrt{3}$
7: $2\sqrt{2}$
解説
(2)
言われた通りに①を使います。角の和を $2$ で割ったものは $x+\dfrac{1}{4}\pi$ で、角の差を $2$ で割ったものは $\dfrac{1}{6}\pi$ なので
\begin{eqnarray}
f(x) &=& \sin \left( x + \dfrac{5}{12}\pi \right) + \sin \left( x + \dfrac{\pi}{12} \right) \\[5pt]
&=&
2\sin \left( x + \dfrac{\pi}{4} \right) \cos \dfrac{\pi}{6} \\[5pt]
\end{eqnarray}となります。
$2\cos\dfrac{\pi}{6}$ は $\sqrt{3}$ です。
$\sin \left( x + \dfrac{\pi}{4} \right)$ は $x=\dfrac{\pi}{4}$ のときに最大値 $1$ をとります。
これらのことから、 $f(x)$ は $x=\dfrac{\pi}{4}$ のときに最大値 $\sqrt{3}\cdot 1=\sqrt{3}$ をとることがわかります。
解答
エオ:32 (2点)
カキ:36 (2点)
解答編 つづき
問題
(3) $a$ を $0 \lt a \lt \pi$ を満たす定数とし、関数 $g(x)$ を
\[ g(x) = \sin (x+a) + \sin (x+2a) + \sin (x+3a) \]とする。
花子さんと太郎さんは、関数 $y=g(x)$ のグラフをコンピュータを用いて表示させてみた。図1は、$a=0.5, a=1.0, a=1.5$ としたときの $y=g(x)$ のグラフである。これを見て、花子さんと太郎さんは、関数 $g(x)$ について話している。
- $g(x)$ は、定数 $p, q$ を用いて $g(x) = p \sin (x+q)$ と変形できそうだね。
- 三つの関数 $\sin (x+a), \sin (x+2a), \sin (x+3a)$ のうちの二つの関数の和に ① を使うと、残り一つの関数の定数倍にできるかな。
(i) ① を用いると、関数 $\sin (x+a), \sin (x+2a), \sin (x+3a)$ のうちの二つの関数の和 $\dBox{ク}$ は、残りの関数 $\sin \left( x + \dBox{ケ} \right)$ の定数倍となる。
したがって、関数 $g(x)$ は
\[ g(x) = \dBox{コ} \sin \left( x + \dbox{ケ} \right) \]と変形することができる。$\dbox{ク}$ の解答群
0: $\sin (x+a) + \sin (x+2a)$
1: $\sin (x+a) + \sin (x+3a)$
2: $\sin (x+2a) + \sin (x+3a)$$\dbox{ケ}$ の解答群
0: $a$
1: $2a$
2: $3a$$\dbox{コ}$ の解答群
0: $2 \cos a$
1: $-2 \cos a$
2: $2 \cos 2a$
3: $-2 \cos 2a$
4: $(2 \cos a + 1)$
5: $(-2 \cos a + 1)$
6: $(2 \cos 2a + 1)$
7: $(-2 \cos 2a + 1)$
解説
(3)(i)
①を使う前提で考えると、角の和の半分を考えることになるので、 $x+a$ と $x+3a$ を使って、 $x+2a$ を作り出すとうまくいきそうだとわかります。
実際に計算すると、角の和の半分は $x+2a$ で差の半分は $a$ なので、
\begin{eqnarray}
& &
\sin (x+3a) +\sin (x+a) \\[5pt]
&=&
2 \sin (x+2a) \cos a \\[5pt]
&=&
2\cos a \sin (x+2a) \\[5pt]
\end{eqnarray}となります。 $2\cos a$ は定数なので、 $\sin (x+2a)$ の定数倍であると言えます。
よって、
\begin{eqnarray}
g(x) &=& \sin (x+a)+\sin (x+2a)+\sin (x+3a) \\[5pt]
&=& 2\cos a \sin (x+2a) +\sin (x+2a) \\[5pt]
&=& (2\cos a +1)\sin (x+2a) \\[5pt]
\end{eqnarray}と表すことができます。
解答
クケ:11 (2点)
コ:4 (2点)
解答編 つづき
問題
(ii) $a = \dfrac{5}{6}\pi$ のとき、$0 \leqq x \lt 2\pi$ の範囲において、$g(x)$ は $x = \dfrac{\myBox{サシ}}{\myBox{ス}}\pi$ で最大値 $\dBox{セ}$ をとる。
$\dbox{セ}$ の解答群
0: $0$
1: $1$
2: $2$
3: $-1$
4: $-2$
5: $\sqrt{3}$
6: $-\sqrt{3}$
7: $\sqrt{3} + 1$
8: $\sqrt{3} - 1$
9: $-\sqrt{3} + 1$
解説
(3)(ii)
$a = \dfrac{5}{6}\pi$ のとき
\begin{eqnarray}
g(x)
&=&
(2\cos a +1)\sin (x+2a) \\[5pt]
&=&
\left(2\cos \frac{5}{6}\pi +1\right)\sin \left(x+\frac{5}{3}\pi \right) \\[5pt]
\end{eqnarray}となります。ここで
\begin{eqnarray}
2\cos \frac{5}{6}\pi +1
&=&
-\sqrt{3}+1
\end{eqnarray}なので負だから、 $g(x)$ が最大となるのは $\sin$ の値が $-1$ となるとき、つまり、 $x=\dfrac{7}{2}\pi-\dfrac{5}{3}\pi=\dfrac{11}{6}\pi$ のときだとわかります。このときの最大値は $\sqrt{3}-1$ となります。
$(2\cos a +1)$ が負であることに気づかないと、間違ってしまうので注意しましょう。
解答
サシス:116 (2点)
セ:8 (2点)