共通テスト 数学II・数学B・数学C 2026年度 第1問 解説

【必答問題】

問題編

問題

　$\mathrm{O}$を原点とする座標平面において、方程式
\[ x^2 + y^2 - 7y + (2x - 5y + 25) = 0 \quad \cdots \text{①} \]の表す円を $C_1$ とする。また、方程式
\[ x^2 + y^2 - 7y - (2x - 5y + 25) = 0 \quad \cdots \text{②} \]の表す円を $C_2$ とする。

(1)　$C_1$ の中心の座標は $\left( \myBox{アイ}, \myBox{ウ} \right)$ である。
　$C_1$ の半径を $r_1$、$C_2$ の半径を $r_2$、$C_1$ の中心と $C_2$ の中心の間の距離を $d$ とすると、$r_1 = \myBox{エ}\sqrt{\myBox{オ}}$, $r_2 = \myBox{カ}\sqrt{\myBox{キ}}$, $d = \sqrt{\myBox{クケ}}$ である。
　$r_1, r_2$ と $d$ の関係から、$C_1$ と $C_2$ は2点で交わることがわかる。

(2)　不等式
\[ x^2 + y^2 - 7y + |2x - 5y + 25| \lt 0 \quad \cdots \text{③} \]の表す領域について考える。
　③ の左辺は、$2x - 5y + 25 \geqq 0$ のときは ① の左辺と一致し、$2x - 5y + 25 \lt 0$ のときは ② の左辺と一致する。

(i)　不等式 $2x - 5y + 25 \geqq 0$ の表す領域を $D$、不等式 $2x - 5y + 25 \lt 0$ の表す領域を $E$ とする。
　・原点 $\mathrm{O}$ は $\dBox{コ}$ に含まれる。
　・$C_1$ の中心は $\dBox{サ}$ に含まれる。
　・$C_2$ の中心は $\dBox{シ}$ に含まれる。

$\dbox{コ}$ ～ $\dbox{シ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $D$
　1: $E$

(ii)　方程式
\[ 2x - 5y + 25 = 0 \quad \cdots \text{④} \]の表す直線を $\ell$ とする。
　実数 $x, y$ が ① と ② の両方を満たすとする。 ① と ② の左辺どうし、右辺どうしの差をとると
\[ 2(2x - 5y + 25) = 0 \]となる。よって、実数 $x, y$ は ④ も満たす。
　したがって、 $\dBox{ス}$ 。このことから、 $\ell$ は $C_1$ と $C_2$ の二つの交点を通る直線であることがわかる。

$\dbox{ス}$ については、最も適当なものを、次の0～5のうちから一つ選べ。

　0: 点 $\mathrm{P}$ を $\ell$ 上の点とすると、$\mathrm{P}$ は $C_1$ 上にあり、かつ $C_2$ 上にもある

　1: 点 $\mathrm{P}$ を $\ell$ 上の点とすると、$\mathrm{P}$ は $C_1$ 上にあるか、または $C_2$ 上にある

　2: 点 $\mathrm{P}$ を $C_1$ 上にあり、かつ $C_2$ 上にもある点とすると、$\mathrm{P}$ は $\ell$ 上にある

　3: 点 $\mathrm{P}$ を $C_1$ 上にあるか、または $C_2$ 上にある点とすると、$\mathrm{P}$ は $\ell$ 上にある

　4: 点 $\mathrm{P}$ を $C_1$ 上の点、点 $\mathrm{Q}$ を $C_2$ 上の点とすると、直線 $\mathrm{PQ}$ は $\ell$ と一致する

　5: 点 $\mathrm{P}$ を $C_1$ 上の点、点 $\mathrm{Q}$ を $C_2$ 上の点とすると、直線 $\mathrm{PQ}$ は $\ell$ と交わる

(iii)　不等式
\[ x^2 + y^2 - 7y + (2x - 5y + 25) \lt 0 \]の表す領域と (i) の領域 $D$ の共通部分を $F$ とする。
　また、不等式
\[ x^2 + y^2 - 7y - (2x - 5y + 25) \lt 0 \]の表す領域と (i) の領域 $E$ の共通部分を $G$ とする。
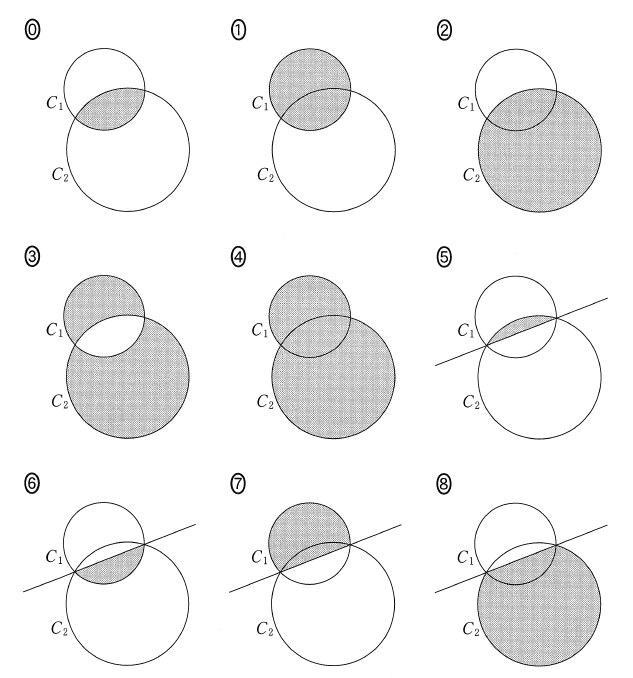
　不等式 ③ の表す領域は、$F$ と $G$ の和集合である。これを図示すると $\myBox{セ}$ の灰色部分である。ただし、境界線を含まない。

(iv)　③ において、$|2x - 5y + 25|$ の前の符号を $+$ から $-$ に変えた不等式
\[ x^2 + y^2 - 7y - |2x - 5y + 25| \lt 0 \quad \cdots \text{⑤} \]を考える。 ⑤ の表す領域を図示すると $\myBox{ソ}$ の灰色部分である。ただし、境界線を含まない。

$\mybox{セ}$、$\mybox{ソ}$ については、最も適当なものを、次の0～8のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、0～8では座標軸を省略している。

考え方

具体的な式が与えられているので、厳密に図をかいて考えることもできますが、ざっくりな図だけで考えることができます。(2)(i)では、ざっくりとどの領域かを判定する方法がヒントとして与えられているので、これを使って (iii) や (iv) を考えましょう。

【必答問題】

解答編

問題

　$\mathrm{O}$を原点とする座標平面において、方程式
\[ x^2 + y^2 - 7y + (2x - 5y + 25) = 0 \quad \cdots \text{①} \]の表す円を $C_1$ とする。また、方程式
\[ x^2 + y^2 - 7y - (2x - 5y + 25) = 0 \quad \cdots \text{②} \]の表す円を $C_2$ とする。

(1)　$C_1$ の中心の座標は $\left( \myBox{アイ}, \myBox{ウ} \right)$ である。
　$C_1$ の半径を $r_1$、$C_2$ の半径を $r_2$、$C_1$ の中心と $C_2$ の中心の間の距離を $d$ とすると、$r_1 = \myBox{エ}\sqrt{\myBox{オ}}$, $r_2 = \myBox{カ}\sqrt{\myBox{キ}}$, $d = \sqrt{\myBox{クケ}}$ である。
　$r_1, r_2$ と $d$ の関係から、$C_1$ と $C_2$ は2点で交わることがわかる。

解説

(1)
\begin{eqnarray} x^2 + y^2 - 7y + (2x - 5y + 25) &=& 0 \\[5pt] x^2+2x + y^2 - 12y &=& -25 \\[5pt] (x+1)^2-1 + (y-6)^2-36 &=& -25 \\[5pt] (x+1)^2 + (y-6)^2 &=& 12 \\[5pt] \end{eqnarray}なので、 $C_1$ の中心の座標は $(-1, 6)$ だとわかります。この半径 $r_1$ は、 $2\sqrt{3}$ です。 \begin{eqnarray} x^2 + y^2 - 7y - (2x - 5y + 25) &=& 0 \\[5pt] x^2-2x + y^2 - 2y &=& 25 \\[5pt] (x-1)^2-1 + (y-1)^2-1 &=& 25 \\[5pt] (x-1)^2 + (y-1)^2 &=& 27 \\[5pt] \end{eqnarray}なので、 $C_2$ の中心の座標は $(1, 1)$ だとわかります。この半径 $r_2$ は、 $3\sqrt{3}$ です。

中心間の距離は
\begin{eqnarray} \sqrt{(-1-1)^2+(6-1)^2} = \sqrt{4+25} =\sqrt{29} \end{eqnarray}なので、\[ |r_1-r_2| \lt d \lt r_1+r_2 \]が成り立つから、2円は2点で交わることがわかります。

解答

アイウ：-16 （2点）
エオカキ：2333 （2点）
クケ：29 （2点）

解答編　つづき

問題

(2)　不等式
\[ x^2 + y^2 - 7y + |2x - 5y + 25| \lt 0 \quad \cdots \text{③} \]の表す領域について考える。
　③ の左辺は、$2x - 5y + 25 \geqq 0$ のときは ① の左辺と一致し、$2x - 5y + 25 \lt 0$ のときは ② の左辺と一致する。

(i)　不等式 $2x - 5y + 25 \geqq 0$ の表す領域を $D$、不等式 $2x - 5y + 25 \lt 0$ の表す領域を $E$ とする。
　・原点 $\mathrm{O}$ は $\dBox{コ}$ に含まれる。
　・$C_1$ の中心は $\dBox{サ}$ に含まれる。
　・$C_2$ の中心は $\dBox{シ}$ に含まれる。

$\dbox{コ}$ ～ $\dbox{シ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $D$
　1: $E$

解説

(2)(i)

$2x-5y+25$ に $x=0,y=0$ を代入すると、 $25$ となります。 $0$ 以上なので、原点は $D$ に含まれます。

$2x-5y+25$ に $x=-1,y=6$ を代入すると、 $-2-30+25=-7$ となります。 $0$ 未満なので、$C_1$ の中心は $E$ に含まれます。

$2x-5y+25$ に $x=1,y=1$ を代入すると、 $2-5+25=22$ となります。 $0$ 以上なので、$C_2$ の中心は $D$ に含まれます。

解答

コサシ：010 （2点）

解答編　つづき

問題

(ii)　方程式
\[ 2x - 5y + 25 = 0 \quad \cdots \text{④} \]の表す直線を $\ell$ とする。
　実数 $x, y$ が ① と ② の両方を満たすとする。 ① と ② の左辺どうし、右辺どうしの差をとると
\[ 2(2x - 5y + 25) = 0 \]となる。よって、実数 $x, y$ は ④ も満たす。
　したがって、 $\dBox{ス}$ 。このことから、 $\ell$ は $C_1$ と $C_2$ の二つの交点を通る直線であることがわかる。

$\dbox{ス}$ については、最も適当なものを、次の0～5のうちから一つ選べ。

　0: 点 $\mathrm{P}$ を $\ell$ 上の点とすると、$\mathrm{P}$ は $C_1$ 上にあり、かつ $C_2$ 上にもある

　1: 点 $\mathrm{P}$ を $\ell$ 上の点とすると、$\mathrm{P}$ は $C_1$ 上にあるか、または $C_2$ 上にある

　2: 点 $\mathrm{P}$ を $C_1$ 上にあり、かつ $C_2$ 上にもある点とすると、$\mathrm{P}$ は $\ell$ 上にある

　3: 点 $\mathrm{P}$ を $C_1$ 上にあるか、または $C_2$ 上にある点とすると、$\mathrm{P}$ は $\ell$ 上にある

　4: 点 $\mathrm{P}$ を $C_1$ 上の点、点 $\mathrm{Q}$ を $C_2$ 上の点とすると、直線 $\mathrm{PQ}$ は $\ell$ と一致する

　5: 点 $\mathrm{P}$ を $C_1$ 上の点、点 $\mathrm{Q}$ を $C_2$ 上の点とすると、直線 $\mathrm{PQ}$ は $\ell$ と交わる

解説

(2)(ii)

問題文にある通り、① と ② の両方を満たしているとき、④ も満たしていることがわかります。

① をみたすことは、対応する点が $C_1$ 上にあることと同値です。② をみたすことは、対応する点が $C_2$ 上にあることと同値です。また、④ をみたすことは、対応する点が $\ell$ 上にあることと同値です。

つまり、式での話を図形の話で言い換えると、「点 $\mathrm{P}$ を $C_1$ 上にあり、かつ $C_2$ 上にもある点とすると、$\mathrm{P}$ は $\ell$ 上にある」ということになります。

なので、問題文にある通り、2円の交点は $\ell$ 上にあるので、 $\ell$ は2円の交点を通る直線だとわかります。

解答

ス：2 （2点）

解答編　つづき

問題

(iii)　不等式
\[ x^2 + y^2 - 7y + (2x - 5y + 25) \lt 0 \]の表す領域と (i) の領域 $D$ の共通部分を $F$ とする。
　また、不等式
\[ x^2 + y^2 - 7y - (2x - 5y + 25) \lt 0 \]の表す領域と (i) の領域 $E$ の共通部分を $G$ とする。
　不等式 ③ の表す領域は、$F$ と $G$ の和集合である。これを図示すると $\myBox{セ}$ の灰色部分である。ただし、境界線を含まない。

(iv)　③ において、$|2x - 5y + 25|$ の前の符号を $+$ から $-$ に変えた不等式
\[ x^2 + y^2 - 7y - |2x - 5y + 25| \lt 0 \quad \cdots \text{⑤} \]を考える。 ⑤ の表す領域を図示すると $\myBox{ソ}$ の灰色部分である。ただし、境界線を含まない。

$\mybox{セ}$、$\mybox{ソ}$ については、最も適当なものを、次の0～8のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、0～8では座標軸を省略している。

解説

(iii)

$F$ とは、次の2つの領域の共通部分です。

　・$2x - 5y + 25 \geqq 0$
　・$x^2 + y^2 - 7y + (2x - 5y + 25) \lt 0$

(2)(i)で見たように、 $C_2$ の中心は1つ目の領域 $D$ に含まれます。直線 $2x-5y+25=0$ は2円の交点を通る直線なので、結局、直線より下の部分に対応することがわかります。

2つ目の領域は、円 $C_1$ の周および内部です。なので、 $F$ は選択肢6に対応します。

$G$ は、次の2つの領域の共通部分です。

　・$2x - 5y + 25 \lt 0$
　・$x^2 + y^2 - 7y - (2x - 5y + 25) \lt 0$

(2)(i)で見たように、 $C_1$ の中心は1つ目の領域 $E$ に含まれます。直線 $2x-5y+25=0$ は2円の交点を通る直線なので、結局、直線より上の部分に対応することがわかります。

2つ目の領域は、円 $C_2$ の周および内部です。なので、 $G$ は選択肢5に対応します。

よって、不等式 ③ に対応するのは、この2つを合わせた選択肢0であることがわかります。

(iv)
$x^2 + y^2 - 7y - |2x - 5y + 25| \lt 0$ は、絶対値の中身で場合分けをすると、

　・$2x - 5y + 25 \geqq 0$
　・$x^2 + y^2 - 7y - (2x - 5y + 25) \lt 0$

の表す領域と

　・$2x - 5y + 25 \lt 0$
　・$x^2 + y^2 - 7y + (2x - 5y + 25) \lt 0$

の表す領域を合わせたものとなります。

先ほどと同じように考えると、1つ目の領域は、直線より下で、円 $C_2$ の内部だから選択肢8に対応し、2つ目の領域は、直線より上で、円 $C_1$ の内部だから選択肢7に対応します。なので、合わせると、選択肢4 だとわかります。

解答

セ：0 （3点）
ソ：4 （2点）