共通テスト 数学II・数学B・数学C 2025年度試作問題 第7問 [2] 解説
2025年度より実施される、新学習指導要領に対応した大学入試共通テストの試作問題(2022年11月発表)です。詳細はこちら。
【第4問~第7問から3問選択】
問題編
問題
太郎さんと花子さんは,複素数 $w$ を一つ決めて,$w,w^2,w^3,\cdots$ によって複素数平面上に表されるそれぞれの点 $\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots$ を表示させたときの様子をコンピュータソフトを用いて観察している。ただし,点 $w$ は実軸より上にあるとする。つまり,$w$ の偏角を $\arg w$ とするとき, $w\ne 0$ かつ $0\lt \arg w \lt \pi$ を満たすとする。
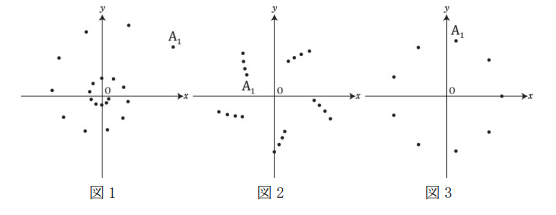
図 1,図 2,図 3 は,$w$ の値を変えて点 $\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots, \mathrm{A}_{20}$ を表示させたものである。ただし,観察しやすくするために,図 1,図 2,図 3 の間では,表示範囲を変えている。
- $𝑤$ の値によって,$\mathrm{A}_1$ から $\mathrm{A}_{20}$ までの点の様子もずいぶんいろいろなパターンがあるね。あれ,図 3 は点が $20$ 個ないよ。
- ためしに $\mathrm{A}_{30}$ まで表示させても図 3 は変化しないね。同じところを何度も通っていくんだと思う。
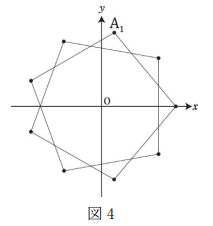
- 図 3 に対して,$\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots $ と線分で結んで点をたどってみると図 4 のようになったよ。なるほど,$\mathrm{A}_{1}$ に戻ってきているね。
図4をもとに,太郎さんは,$\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots $ と点をとっていって再び $\mathrm{A}_1$ に戻る場合に,点を順に線分で結んでできる図形について一般に考えることにした。すなわち,$\mathrm{A}_1$ と $\mathrm{A}_n$ が重なるような $n$ があるとき,線分 $\mathrm{A}_1\mathrm{A}_2$ ,$\mathrm{A}_2\mathrm{A}_3$,$\cdots$, $\mathrm{A}_{n-1}\mathrm{A}_n$ をかいてできる図形について考える。このとき,$w=w^n$ に着目すると $|w|=\myBox{イ}$ であることがわかる。また,次のことが成り立つ。
- $1\leqq k\leqq n-1$ に対して $\mathrm{A}_k\mathrm{A}_{k+1}=\dBox{ウ}$ であり,つねに一定である。
- $2\leqq k\leqq n-1$ に対して $\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}=\dBox{エ}$ であり,つねに一定である。 ただし,$\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}$ は,線分 $\mathrm{A}_k\mathrm{A}_{k+1}$ を線分 $\mathrm{A}_k\mathrm{A}_{k-1}$ に重なるまで回転させた角とする。
花子さんは,$n=25$ のとき,すなわち, $\mathrm{A}_1$ と $\mathrm{A}_{25}$ が重なるとき,$\mathrm{A}_1$ から $\mathrm{A}_{25}$ までを順に線分で結んでできる図形が,正多角形になる場合を考えた。このような $w$ の値は全部で $\myBox{オ}$ 個である。また,このような正多角形についてどの場合であっても,それぞれの正多角形に内接する円上の点を $z$ とすると,$z$ はつねに $\dBox{カ}$ を満たす。
$\dbox{ウ}$ の解答群
0: $|w+1|$
1: $|w-1|$
2: $|w|+1$
3: $|w|-1$$\dbox{エ}$ の解答群
0: $\arg w$
1: $\arg (-w)$2: $\arg \dfrac{1}{w}$
3: $\arg \left(-\dfrac{1}{w}\right)$
$\dbox{カ}$ の解答群
0: $|z|=1$
1: $|z-w|=1$
2: $|z|=|w+1|$
3: $|z|=|w-1|$
4: $|z-w|=|w+1|$
5: $|z-w|=|w-1|$6: $|z|=\dfrac{|w+1|}{2}$
7: $|z|=\dfrac{|w-1|}{2}$
考え方
新しく数学Cの分野が追加されました。複素数平面からは、図形と絡めた問題です。後半は図形の扱いに慣れていないと少し難しく感じるかもしれません。
【第4問~第7問から3問選択】
解答編
問題
太郎さんと花子さんは,複素数 $w$ を一つ決めて,$w,w^2,w^3,\cdots$ によって複素数平面上に表されるそれぞれの点 $\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots$ を表示させたときの様子をコンピュータソフトを用いて観察している。ただし,点 $w$ は実軸より上にあるとする。つまり,$w$ の偏角を $\arg w$ とするとき, $w\ne 0$ かつ $0\lt \arg w \lt \pi$ を満たすとする。
図 1,図 2,図 3 は,$w$ の値を変えて点 $\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots, \mathrm{A}_{20}$ を表示させたものである。ただし,観察しやすくするために,図 1,図 2,図 3 の間では,表示範囲を変えている。
- $𝑤$ の値によって,$\mathrm{A}_1$ から $\mathrm{A}_{20}$ までの点の様子もずいぶんいろいろなパターンがあるね。あれ,図 3 は点が $20$ 個ないよ。
- ためしに $\mathrm{A}_{30}$ まで表示させても図 3 は変化しないね。同じところを何度も通っていくんだと思う。
- 図 3 に対して,$\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots $ と線分で結んで点をたどってみると図 4 のようになったよ。なるほど,$\mathrm{A}_{1}$ に戻ってきているね。
図4をもとに,太郎さんは,$\mathrm{A}_1,\mathrm{A}_2,\mathrm{A}_3,\cdots $ と点をとっていって再び $\mathrm{A}_1$ に戻る場合に,点を順に線分で結んでできる図形について一般に考えることにした。すなわち,$\mathrm{A}_1$ と $\mathrm{A}_n$ が重なるような $n$ があるとき,線分 $\mathrm{A}_1\mathrm{A}_2$ ,$\mathrm{A}_2\mathrm{A}_3$,$\cdots$, $\mathrm{A}_{n-1}\mathrm{A}_n$ をかいてできる図形について考える。このとき,$w=w^n$ に着目すると $|w|=\myBox{イ}$ であることがわかる。
解説
$w=w^n$ より、 $|w|=|w^n|=|w|^n$ が成り立ちます。 $w\ne 0$ なので、 $|w|^{n-1}=1$ となります。 $|w|$ は $0$ 以上の実数なので、 $|w|=1$ とわかります。
解答
イ:1
解答編 つづき
問題
また,次のことが成り立つ。
- $1\leqq k\leqq n-1$ に対して $\mathrm{A}_k\mathrm{A}_{k+1}=\dBox{ウ}$ であり,つねに一定である。
- $2\leqq k\leqq n-1$ に対して $\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}=\dBox{エ}$ であり,つねに一定である。 ただし,$\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}$ は,線分 $\mathrm{A}_k\mathrm{A}_{k+1}$ を線分 $\mathrm{A}_k\mathrm{A}_{k-1}$ に重なるまで回転させた角とする。
$\dbox{ウ}$ の解答群
0: $|w+1|$
1: $|w-1|$
2: $|w|+1$
3: $|w|-1$$\dbox{エ}$ の解答群
0: $\arg w$
1: $\arg (-w)$2: $\arg \dfrac{1}{w}$
3: $\arg \left(-\dfrac{1}{w}\right)$
解説
$\mathrm{A}_0$ を $1$ に対応する点だとすると、線分 $\mathrm{A}_k\mathrm{A}_{k-1}$ の長さは、線分 $\mathrm{A}_1\mathrm{A}_0$ の長さと等しいです。 $\mathrm{A}_1,\mathrm{A}_0$ は、それぞれ、 $w,1$ を表しているので、線分 $\mathrm{A}_1\mathrm{A}_0$ の長さは $|w-1|$ となります。
$\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}$ は、 $\angle\mathrm{A}_2\mathrm{A}_1\mathrm{A}_0$ と等しいです。 $\mathrm{A}_2,\mathrm{A}_1,\mathrm{A}_0$ は、それぞれ、 $w^2,w,1$ を表しています。問題文にあるように、「線分 $\mathrm{A}_k\mathrm{A}_{k+1}$ を線分 $\mathrm{A}_k\mathrm{A}_{k-1}$ に重なるまで回転させた角」とあるので、 $\mathrm{A}_1$ を中心として、 $\mathrm{A}_2$ を $\mathrm{A}_0$ に重ねるように動かせばいいことから、 $\angle\mathrm{A}_2\mathrm{A}_1\mathrm{A}_0$ は
\begin{eqnarray}
\arg \frac{1-w}{w^2-w}=\arg \frac{-(w-1)}{w(w-1)} =\arg \left(-\frac{1}{w}\right)
\end{eqnarray}と求められます。(ちなみに、条件に $0\lt\arg w\lt\pi$ とあるので、 $w\ne 1$ だから、上の式の分数の分母は $0$ ではありません)
解答
ウ:1
エ:3
解答編 つづき
問題
花子さんは,$n=25$ のとき,すなわち, $\mathrm{A}_1$ と $\mathrm{A}_{25}$ が重なるとき,$\mathrm{A}_1$ から $\mathrm{A}_{25}$ までを順に線分で結んでできる図形が,正多角形になる場合を考えた。このような $w$ の値は全部で $\myBox{オ}$ 個である。また,このような正多角形についてどの場合であっても,それぞれの正多角形に内接する円上の点を $z$ とすると,$z$ はつねに $\dBox{カ}$ を満たす。
$\dbox{カ}$ の解答群
0: $|z|=1$
1: $|z-w|=1$
2: $|z|=|w+1|$
3: $|z|=|w-1|$
4: $|z-w|=|w+1|$
5: $|z-w|=|w-1|$6: $|z|=\dfrac{|w+1|}{2}$
7: $|z|=\dfrac{|w-1|}{2}$
解説
まず、 $w^1=w^{25}$ を満たすので、 $w^{24}=1$ が成り立たないといけません。よって、少なくとも、 $w=\cos\frac{m\pi}{12}+i \sin\frac{m\pi}{12}$ $(m=1,2,\cdots,24)$ と書けます。条件 $0\lt \arg w\lt \pi$ より、 $m=1,2,\cdots, 11$ にしぼられます。
これらがすべて条件を満たすわけではありません。図4のようになっていれば、 $\mathrm{A}_1$ と $\mathrm{A}_n$ は重なっていますが、正多角形にはなっていません。そこで、$\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}$ に注目して、これが正多角形の内角になるようなものを選ぶようにします。
$\angle\mathrm{A}_{k+1}\mathrm{A}_k\mathrm{A}_{k-1}$ は $\arg \left(-\frac{1}{w}\right)$ なので、 $w=\cos\frac{m\pi}{12}+i \sin\frac{m\pi}{12}$ のときは、 $\frac{m}{12}\pi$ となります。正三角形の場合、内角は $60^{\circ}$ なので、 $m=4$ となります。他の正多角形の内角は $60^{\circ}$ より大きいので、 $m=4,5,6,\cdots,11$ にしぼられます。
他の $m$ に対して正多角形が存在するかは、次のように考えます。内角が $\frac{m}{12}\pi$ のとき、外角は $\pi-\frac{m}{12}\pi$ です。外角の和は $2\pi$ なので、\[ 2\pi \div \left(\pi-\frac{m}{12}\pi\right)=\frac{2}{1-\frac{m}{12}}=\frac{24}{12-m} \]が整数にならないといけません。これより、 $m=4,6,8,9,10,11$ だとわかります。具体的には、
$m=4$ のとき:正三角形(内角 $60^{\circ}$)
$m=6$ のとき:正方形(内角 $90^{\circ}$)
$m=8$ のとき:正六角形(内角 $120^{\circ}$)
$m=9$ のとき:正八角形(内角 $135^{\circ}$)
$m=10$ のとき:正12角形(内角 $150^{\circ}$)
$m=11$ のとき:正24角形(内角 $165^{\circ}$)
となります。
出来上がった正多角形に内接する円は、必ず正多角形の辺の中点で接します。なので、辺の中点と原点との距離は、円の半径と一致します。辺 $\mathrm{A}_1\mathrm{A}_0$ の中点は $\frac{w+1}{2}$ なので、\[ |z|=\frac{|w+1|}{2} \]が成り立ちます。
解答
オ:6
カ:6