共通テスト 数学II・数学B・数学C 2025年度 第7問 解説

【第4問～第7問から3問選択】

問題編

問題

　$\alpha,\ \beta,\ \gamma$ を異なる複素数とし、複素数平面上に $3$ 点 $\mathrm{A}(\alpha), \mathrm{B}(\beta), \mathrm{C}(\gamma)$ をとる。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ の関係について考えよう。
　以下、複素数の偏角は $0$ 以上 $2\pi$ 未満とする。

(1) $\alpha = 3+2i,\ \beta = 7,\ \gamma = 7+10i$ の場合を考える。$\dfrac{\gamma - \alpha}{\beta - \alpha}$ の偏角を求めよう。
\begin{eqnarray} \gamma - \alpha = \myBox{ア} + \myBox{イ} i \\[5pt] \beta - \alpha = \myBox{ウ} - \myBox{エ} i \end{eqnarray}であるから \[ \dfrac{\gamma - \alpha}{\beta - \alpha} = \dBox{オ} \]であり、$\dbox{オ}$ の偏角は $\dBox{カ}$ である。

$\dbox{オ}$ の解答群
　0: $i$
　1: $1+i$
　2: $2$
　3: $2i$
　4: $-i$
　5: $1-i$
　6: $-2$
　7: $-2i$

$\dbox{カ}$ の解答群
　0: $0$

　1: $\dfrac{\pi}{6}$

　2: $\dfrac{\pi}{4}$

　3: $\dfrac{\pi}{3}$

　4: $\dfrac{\pi}{2}$

　5: $\dfrac{3}{4}\pi$

　6: $\pi$

　7: $\dfrac{5}{4}\pi$

　8: $\dfrac{3}{2}\pi$

　9: $\dfrac{7}{4}\pi$

(2) $w = \dfrac{\gamma - \alpha}{\beta - \alpha}$ とおく。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるのは、$w$ の偏角が $\dfrac{\pi}{2}$ または $\dfrac{3}{2}\pi$ のときである。このとき、$w$ は $\dBox{キ}$ であるから
\[ w + \overline{w} = \dBox{ク} \]である。逆に、$w \neq 0$ に注意すると、$w + \overline{w} = \dbox{ク}$ のとき、$w$ は $\dbox{キ}$ であるので、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わる。

$\dbox{キ}$ の解答群
　0: $0$ でない実数
　1: $1+i$ または $1-i$
　2: 純虚数（実部が $0$ である虚数）
　3: $-1+i$ または $-1-i$

$\dbox{ク}$ の解答群
　0: $0$
　1: $1$
　2: $2$
　3: $i$
　4: $2i$
　5: $-1$
　6: $-2$
　7: $-i$

(3) $z$ は $0, 2, -2$ でない複素数とする。

(i) $\alpha = z, \beta = 2, \gamma = \dfrac{4}{z}$ とする。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための条件について考えよう。
\[ \dfrac{\gamma - \alpha}{\beta - \alpha} = \dfrac{\frac{4}{z} - z}{2 - z} = 1 + \dfrac{2}{z} \]
が成り立つので、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための必要十分条件は
\[ \left( 1 + \dfrac{2}{z} \right) + \overline{\left( 1 + \dfrac{2}{z} \right)} = \dbox{ク} \]である。これは
\[ 2 + \dfrac{2}{z} + \dfrac{2}{\overline{z}} = \dbox{ク} \]と変形できる。さらに、この両辺に $z\overline{z}$ をかけて整理すると、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための必要十分条件は $\dBox{ケ}$ であることがわかる。したがって、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるような点 $z$ 全体を複素数平面上に図示すると $\dBox{コ}$ である。

$\dbox{ケ}$ の解答群
　0: $|z| = |z-4|$
　1: $|z| = |z-2|$
　2: $|z| = |z+4|$
　3: $|z+1| = |z-1|$
　4: $|z-1| = 1$
　5: $|z| = 2$
　6: $|z+1| = 1$
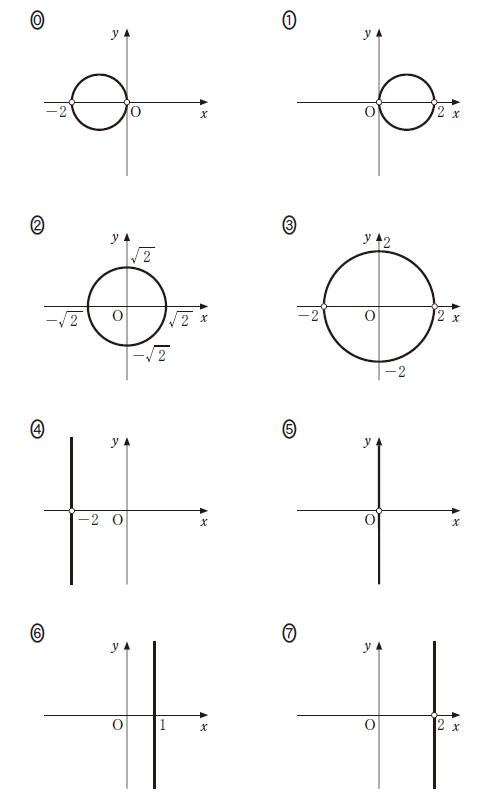
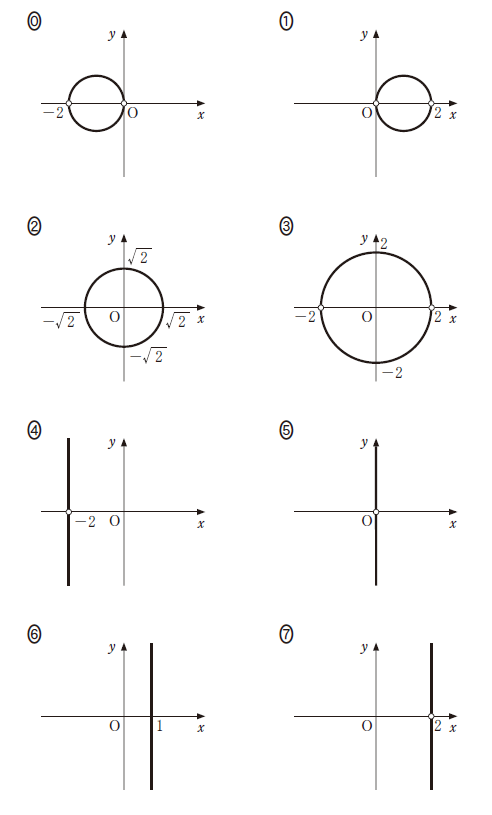
　7: $|z| = \sqrt{2}$

$\dbox{コ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つ選べ。

(ii) (i) の $\alpha, \beta, \gamma$ をそれぞれ $-1$ 倍した複素数 $\alpha' = -z, \beta' = -2, \gamma' = -\dfrac{4}{z}$ について考える。複素数平面上の異なる $3$ 点 $\mathrm{A}'(\alpha'), \mathrm{B}'(\beta'), \mathrm{C}'(\gamma')$ について、直線 $\mathrm{A}'\mathrm{B}'$ と直線 $\mathrm{A}'\mathrm{C}'$ が垂直になるような点 $z$ 全体を複素数平面上に図示すると $\dBox{サ}$ である。

(iii) (i) の $\alpha, \beta, \gamma$ における $z$ を $-z$ に置き換え、$\alpha'' = -z, \beta'' = 2, \gamma'' = -\dfrac{4}{z}$ について考える。複素数平面上の異なる $3$ 点 $\mathrm{A}''(\alpha''), \mathrm{B}''(\beta''), \mathrm{C}''(\gamma'')$ について、直線 $\mathrm{A}''\mathrm{B}''$ と直線 $\mathrm{A}''\mathrm{C}''$ が垂直になるような点 $z$ 全体を複素数平面上に図示すると $\dBox{シ}$ である。

$\dbox{サ},$ $\dbox{シ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

考え方

(1)は基本的な複素数の計算です。(2)は誘導に従って計算していきます。(3)(i)は複素数で図形を表すときによくやる変形をします。(ii)と(iii)は、一から考えずに、どの条件がどのように変わるかを考えましょう。

【第4問～第7問から3問選択】

解答編

問題

　$\alpha,\ \beta,\ \gamma$ を異なる複素数とし、複素数平面上に $3$ 点 $\mathrm{A}(\alpha), \mathrm{B}(\beta), \mathrm{C}(\gamma)$ をとる。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ の関係について考えよう。
　以下、複素数の偏角は $0$ 以上 $2\pi$ 未満とする。

(1) $\alpha = 3+2i,\ \beta = 7,\ \gamma = 7+10i$ の場合を考える。$\dfrac{\gamma - \alpha}{\beta - \alpha}$ の偏角を求めよう。
\begin{eqnarray} \gamma - \alpha = \myBox{ア} + \myBox{イ} i \\[5pt] \beta - \alpha = \myBox{ウ} - \myBox{エ} i \end{eqnarray}であるから \[ \dfrac{\gamma - \alpha}{\beta - \alpha} = \dBox{オ} \]であり、$\dbox{オ}$ の偏角は $\dBox{カ}$ である。

$\dbox{オ}$ の解答群
　0: $i$
　1: $1+i$
　2: $2$
　3: $2i$
　4: $-i$
　5: $1-i$
　6: $-2$
　7: $-2i$

$\dbox{カ}$ の解答群
　0: $0$

　1: $\dfrac{\pi}{6}$

　2: $\dfrac{\pi}{4}$

　3: $\dfrac{\pi}{3}$

　4: $\dfrac{\pi}{2}$

　5: $\dfrac{3}{4}\pi$

　6: $\pi$

　7: $\dfrac{5}{4}\pi$

　8: $\dfrac{3}{2}\pi$

　9: $\dfrac{7}{4}\pi$

解説

(1)
\begin{eqnarray} \gamma-\alpha &=& (7+10i)-(3+2i) \\[5pt] &=& 4+8i \\[5pt] \\ \beta-\alpha &=& 7-(3+2i) \\[5pt] &=& 4-2i \\[5pt] \end{eqnarray}なので \begin{eqnarray} \frac{\gamma-\alpha}{\beta-\alpha} &=& \frac{4+8i}{4-2i} \\[5pt] &=& \frac{(4+8i)(4+2i)}{4^2+2^2} \\[5pt] &=& \frac{16-16+i(32+8)}{20} \\[5pt] &=& 2i \\[5pt] \end{eqnarray}です。偏角は $\dfrac{\pi}{2}$ です。

解答

アイウエ：4842
オ：3
カ：4

解答編　つづき

問題

(2) $w = \dfrac{\gamma - \alpha}{\beta - \alpha}$ とおく。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるのは、$w$ の偏角が $\dfrac{\pi}{2}$ または $\dfrac{3}{2}\pi$ のときである。このとき、$w$ は $\dBox{キ}$ であるから
\[ w + \overline{w} = \dBox{ク} \]である。逆に、$w \neq 0$ に注意すると、$w + \overline{w} = \dbox{ク}$ のとき、$w$ は $\dbox{キ}$ であるので、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わる。

$\dbox{キ}$ の解答群
　0: $0$ でない実数
　1: $1+i$ または $1-i$
　2: 純虚数（実部が $0$ である虚数）
　3: $-1+i$ または $-1-i$

$\dbox{ク}$ の解答群
　0: $0$
　1: $1$
　2: $2$
　3: $i$
　4: $2i$
　5: $-1$
　6: $-2$
　7: $-i$

解説

(2) $w$ の偏角が $\dfrac{\pi}{2}$ または $\dfrac{3}{2}\pi$ のとき、 $w$ は純虚数なので、 $\overline{w}=-w$ だから、\[ w+\overline{w}=0 \]となります。逆に、 $w\ne 0$ のときに $w+\overline{w}=0$ ならば、 $w$ は純虚数であり、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わります。

解答

キク：20

解答編　つづき

問題

(3) $z$ は $0, 2, -2$ でない複素数とする。

(i) $\alpha = z, \beta = 2, \gamma = \dfrac{4}{z}$ とする。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための条件について考えよう。
\[ \dfrac{\gamma - \alpha}{\beta - \alpha} = \dfrac{\frac{4}{z} - z}{2 - z} = 1 + \dfrac{2}{z} \]
が成り立つので、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための必要十分条件は
\[ \left( 1 + \dfrac{2}{z} \right) + \overline{\left( 1 + \dfrac{2}{z} \right)} = \dbox{ク} \]である。これは
\[ 2 + \dfrac{2}{z} + \dfrac{2}{\overline{z}} = \dbox{ク} \]と変形できる。さらに、この両辺に $z\overline{z}$ をかけて整理すると、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための必要十分条件は $\dBox{ケ}$ であることがわかる。したがって、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるような点 $z$ 全体を複素数平面上に図示すると $\dBox{コ}$ である。

$\dbox{ケ}$ の解答群
　0: $|z| = |z-4|$
　1: $|z| = |z-2|$
　2: $|z| = |z+4|$
　3: $|z+1| = |z-1|$
　4: $|z-1| = 1$
　5: $|z| = 2$
　6: $|z+1| = 1$
　7: $|z| = \sqrt{2}$

$\dbox{コ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つ選べ。

解説

(3)(i)
\begin{eqnarray} \frac{\gamma-\alpha}{\beta-\alpha} &=& \frac{\frac{4}{z}-z}{2-z} \\[5pt] &=& \frac{4-z^2}{z(2-z)} \\[5pt] &=& \frac{(2+z)(2-z)}{z(2-z)} \\[5pt] &=& 1+\frac{2}{z} \\[5pt] \end{eqnarray}なので、(2)で見たように、直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるための必要十分条件は \begin{eqnarray} \left(1+\frac{2}{z}\right)+\overline{\left(1+\frac{2}{z}\right)} &=& 0 \\[5pt] 2+\frac{2}{z}+\frac{2}{\bar{z}} &=& 0 \\[5pt] z\bar{z}+\bar{z}+z &=& 0 \\[5pt] (z+1)\overline{(z+1)} &=& 1 \\[5pt] |z+1| &=& 1 \\[5pt] \end{eqnarray}となります。問題文の最初にあるように、 $z$ は $0,2,-2$ ではないので、点 $z$ 全体を図示すると、 $-1$ を中心とする半径 $1$ の円のうち、 $0,-2$ を除いたもの、となります。選択肢の中では、0 となります。

ちなみに、 $z\ne 0$ という条件は、 $\gamma$ を定義するため、 $z\ne 2$ という条件は $\alpha\ne\beta$ のため、 $z\ne -2$ は $\alpha\ne\gamma$ とするためです（2点が一致すると、直線がひけないためです）。

解答

ケ：6
コ：0

解答編　つづき

問題

(ii) (i) の $\alpha, \beta, \gamma$ をそれぞれ $-1$ 倍した複素数 $\alpha' = -z, \beta' = -2, \gamma' = -\dfrac{4}{z}$ について考える。複素数平面上の異なる $3$ 点 $\mathrm{A}'(\alpha'), \mathrm{B}'(\beta'), \mathrm{C}'(\gamma')$ について、直線 $\mathrm{A}'\mathrm{B}'$ と直線 $\mathrm{A}'\mathrm{C}'$ が垂直になるような点 $z$ 全体を複素数平面上に図示すると $\dBox{サ}$ である。

解説

(3)(ii)

$-1$ 倍すると、原点を中心に 180度回転することになります。つまり、三角形 $\mathrm{A'B'C'}$ は、三角形 $\mathrm{ABC}$ を回転したものだから合同なので、直線 $\mathrm{A'B'}$ と直線 $\mathrm{A'C'}$ が垂直に交わることと直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わることは同値です。つまり、この場合も、$z$ を図示すると、(i)と同じ結果になります。

解答

サ：0

解答編　つづき

問題

(iii) (i) の $\alpha, \beta, \gamma$ における $z$ を $-z$ に置き換え、$\alpha'' = -z, \beta'' = 2, \gamma'' = -\dfrac{4}{z}$ について考える。複素数平面上の異なる $3$ 点 $\mathrm{A}''(\alpha''), \mathrm{B}''(\beta''), \mathrm{C}''(\gamma'')$ について、直線 $\mathrm{A}''\mathrm{B}''$ と直線 $\mathrm{A}''\mathrm{C}''$ が垂直になるような点 $z$ 全体を複素数平面上に図示すると $\dBox{シ}$ である。

$\dbox{サ},$ $\dbox{シ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

解説

(3)(iii)

(i)で得られた式 $|z+1|=1$ で $z$ を $-z$ にすればいいので、 $|-z+1|=1$ 、つまり、 $|z-1|=1$ です。これを図示すると、選択肢 1 のグラフになります。

解答

シ：1