共通テスト 数学II・数学B・数学C 2025年度 第4問 解説

【第4問～第7問から3問選択】

問題編

問題

　座標平面上で、$x$ 座標と $y$ 座標がともに整数である点を格子点という。いくつかの直線や曲線で囲まれた図形の内部にある格子点の個数を考えよう。ただし、図形の内部は、境界（境界線）を含まないものとする。
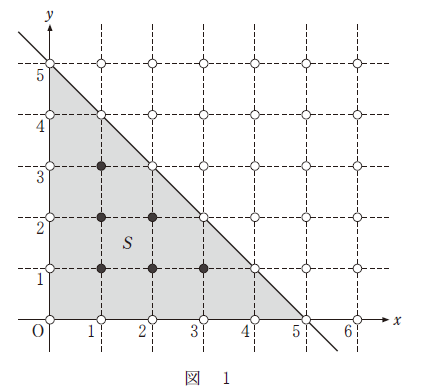
　例えば、直線 $y = -x + 5$ と $x$ 軸、$y$ 軸で囲まれた図形を $S$ とする。$S$ は図1の灰色部分であり、$S$ の内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、$S$ の内部にある格子点の個数は $6$ である。

(1) 直線 $y = 3x$ と $x$ 軸、直線 $x = 21$ で囲まれた図形を $T$ とする。$T$ の内部にある格子点の個数を考える。
　直線 $x = 1$ 上の格子点で $T$ の内部にあるものは、点 $(1, 1)$ と点 $(1, 2)$ の $2$ 個である。点 $(1, 0)$ と点 $(1, 3)$ は $T$ の境界にあるため、内部にはない。
　$n$ を整数とする。直線 $x = n$ が $T$ の内部にある格子点を通るのは、$1 \leqq n \leqq 20$ のときである。$1 \leqq n \leqq 20$ のとき、直線 $x = n$ 上の格子点で $T$ の内部にあるものの個数を $a_n$ とおく。$a_1 = 2$ であり、$a_2 = \myBox{ア}$ 、 $a_3 = \myBox{イ}$ である。数列 $\{a_n\}$ は $\dBox{ウ}$ が $\myBox{エ}$ の $\dBox{オ}$ 数列である。
　したがって、$T$ の内部にある格子点の個数は $\myBox{カキク}$ である。

$\dbox{ウ}$ の解答群
　0: 公 差
　1: 公 比

$\dbox{オ}$ の解答群
　0: 等 差
　1: 等 比

(2) $n$ を自然数とする。関数 $y = 2^x$ のグラフと $x$ 軸、$y$ 軸および直線 $x = n + 1$ で囲まれた図形を $U$ とする。
　$k$ を整数とする。直線 $x = k$ が $U$ の内部にある格子点を通るとき、直線 $x = k$ 上の格子点で $U$ の内部にあるものの個数は $\dBox{ケ}$ である。
　したがって、$U$ の内部にある格子点の個数は
\[ \sum_{k=1}^{\dBox{コ}} \left( \dbox{ケ} \right) = \dBox{サ} \]である。

$\dbox{ケ}$ の解答群
　0: $2k - 2$
　1: $2k - 1$
　2: $2k$
　3: $2^{k-1} - 2$
　4: $2^{k-1} - 1$
　5: $2^{k-1}$
　6: $2^k - 2$
　7: $2^k - 1$
　8: $2^k$

$\dbox{コ}$ の解答群
　0: $n - 1$
　1: $n$
　2: $n + 1$
　3: $2n - 1$
　4: $2n$
　5: $2n + 1$
　6: $2^n - 1$
　7: $2^n$
　8: $2^n + 1$

$\dBox{サ}$ の解答群
　0: $2^n - 2n - 1$
　1: $2^n - 2n$
　2: $2^n - n - 1$
　3: $2^n - n$
　4: $2^n - 3$
　5: $2^{n+1} - 2n - 2$
　6: $2^{n+1} - 2n - 1$
　7: $2^{n+1} - n - 2$
　8: $2^{n+1} - n - 1$
　9: $2^{n+1} - 3$

(3) $a$、$b$、$c$ は整数で、$a \gt 0$、$b^2 - 4ac \lt 0$ を満たすとする。放物線 $y = ax^2 + bx + c$ と $x$ 軸、$y$ 軸および直線 $x = n + 1$ で囲まれた図形を $V$ とする。すべての自然数 $n$ に対して、$V$ の内部にある格子点の個数が $n^3$ となるのは、$a = \myBox{シ}$ 、 $b = \myBox{スセ}$ 、 $c = \myBox{ソ}$ のときである。

考え方

まず、(1)で何を計算しないといけないか、グラフを使って考えます。その法則を使って、(2)を考えます。ケ の部分が 1 ズレただけで計算が狂ってくるので慎重に考えましょう。

(3)では、条件があるとグラフがどうなっているかをまず考えます。そのあとは(2)と同じように考えます。少し計算が必要です。

【第4問～第7問から3問選択】

解答編

問題

　座標平面上で、$x$ 座標と $y$ 座標がともに整数である点を格子点という。いくつかの直線や曲線で囲まれた図形の内部にある格子点の個数を考えよう。ただし、図形の内部は、境界（境界線）を含まないものとする。
　例えば、直線 $y = -x + 5$ と $x$ 軸、$y$ 軸で囲まれた図形を $S$ とする。$S$ は図1の灰色部分であり、$S$ の内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、$S$ の内部にある格子点の個数は $6$ である。

(1) 直線 $y = 3x$ と $x$ 軸、直線 $x = 21$ で囲まれた図形を $T$ とする。$T$ の内部にある格子点の個数を考える。
　直線 $x = 1$ 上の格子点で $T$ の内部にあるものは、点 $(1, 1)$ と点 $(1, 2)$ の $2$ 個である。点 $(1, 0)$ と点 $(1, 3)$ は $T$ の境界にあるため、内部にはない。
　$n$ を整数とする。直線 $x = n$ が $T$ の内部にある格子点を通るのは、$1 \leqq n \leqq 20$ のときである。$1 \leqq n \leqq 20$ のとき、直線 $x = n$ 上の格子点で $T$ の内部にあるものの個数を $a_n$ とおく。$a_1 = 2$ であり、$a_2 = \myBox{ア}$ 、 $a_3 = \myBox{イ}$ である。数列 $\{a_n\}$ は $\dBox{ウ}$ が $\myBox{エ}$ の $\dBox{オ}$ 数列である。
　したがって、$T$ の内部にある格子点の個数は $\myBox{カキク}$ である。

$\dbox{ウ}$ の解答群
　0: 公 差
　1: 公 比

$\dbox{オ}$ の解答群
　0: 等 差
　1: 等 比

解説

(1)
$x=2$ 上にある格子点の個数は、 $0$ より大きく、 $3\cdot 2=6$ より小さい整数の個数なので、 $5$ 個だから、 $a_2=5$ です。

$x=3$ 上にある格子点の個数は、 $0$ より大きく、 $3\cdot 3=9$ より小さい整数の個数なので、 $8$ 個だから、 $a_3=8$ です。

$x=n$ の $n$ が増えるたびに、3個ずつ増えるので、数列 $\{a_n\}$ は公差が $3$ の等差数列です。これより、一般項は\[ a_n=2+3(n-1)=3n-1 \]となります。

これを使うと、 $T$ の内部にある格子点の個数は
\begin{eqnarray} & & \sum_{k=1}^{20} (3k-1) \\[5pt] &=& 3\cdot\frac{20\cdot 21}{2}-20 \\[5pt] &=& 630-20 \\[5pt] &=& 610 \\[5pt] \end{eqnarray}と求められます。

解答

アイ：58
ウエオ：030
カキク：610

解答編　つづき

問題

(2) $n$ を自然数とする。関数 $y = 2^x$ のグラフと $x$ 軸、$y$ 軸および直線 $x = n + 1$ で囲まれた図形を $U$ とする。
　$k$ を整数とする。直線 $x = k$ が $U$ の内部にある格子点を通るとき、直線 $x = k$ 上の格子点で $U$ の内部にあるものの個数は $\dBox{ケ}$ である。
　したがって、$U$ の内部にある格子点の個数は
\[ \sum_{k=1}^{\dBox{コ}} \left( \dbox{ケ} \right) = \dBox{サ} \]である。

$\dbox{ケ}$ の解答群
　0: $2k - 2$
　1: $2k - 1$
　2: $2k$
　3: $2^{k-1} - 2$
　4: $2^{k-1} - 1$
　5: $2^{k-1}$
　6: $2^k - 2$
　7: $2^k - 1$
　8: $2^k$

$\dbox{コ}$ の解答群
　0: $n - 1$
　1: $n$
　2: $n + 1$
　3: $2n - 1$
　4: $2n$
　5: $2n + 1$
　6: $2^n - 1$
　7: $2^n$
　8: $2^n + 1$

$\dBox{サ}$ の解答群
　0: $2^n - 2n - 1$
　1: $2^n - 2n$
　2: $2^n - n - 1$
　3: $2^n - n$
　4: $2^n - 3$
　5: $2^{n+1} - 2n - 2$
　6: $2^{n+1} - 2n - 1$
　7: $2^{n+1} - n - 2$
　8: $2^{n+1} - n - 1$
　9: $2^{n+1} - 3$

解説

(2)
直線 $x=k$ 上にある格子点の個数は、 $0$ より大きく $2^k$ より小さい整数の個数と同じなので、 $2^k-1$ だとわかります。

これを、 $k=1$ から $k=n$ まで足せば、 $U$ の内部ある格子点の個数がわかるので
\begin{eqnarray} & & \sum_{k=1}^n (2^k-1) \\[5pt] &=& \frac{2(2^n-1)}{2-1} -n \\[5pt] &=& 2^{n+1}-2 -n \\[5pt] \end{eqnarray}なので、 $2^{n+1}-n-2$ となることがわかります。

解答

ケ：7
コ：1
サ：7

解答編　つづき

問題

(3) $a$、$b$、$c$ は整数で、$a \gt 0$、$b^2 - 4ac \lt 0$ を満たすとする。放物線 $y = ax^2 + bx + c$ と $x$ 軸、$y$ 軸および直線 $x = n + 1$ で囲まれた図形を $V$ とする。すべての自然数 $n$ に対して、$V$ の内部にある格子点の個数が $n^3$ となるのは、$a = \myBox{シ}$ 、 $b = \myBox{スセ}$ 、 $c = \myBox{ソ}$ のときである。

解説

(3)
$a\gt 0$ と $b^2-4ac\lt 0$ という条件から、 $y=ax^2+bx+c$ のグラフは下に凸で、 $x$ 軸とは交わらないことがわかります。なので、 $V$ の内部で $x=k$ 上にある格子点の個数は、 $0$ より大きく $ak^2+bk+c$ という整数より小さい整数の個数と一致するので、\[ ak^2+bk+c-1 \]となります。

これを $k=1$ から $k=n$ まで足したものが格子点の個数となります。
\begin{eqnarray} & & \sum_{k=1}^n (ak^2+bk+c-1) \\[5pt] &=& \frac{an(n+1)(2n+1)}{6}+\frac{bn(n+1)}{2}+n(c-1) \\[5pt] &=& n \left\{\frac{a(2n^2+3n+1)}{6}+\frac{b(n+1)}{2}+(c-1) \right\} \\[5pt] \end{eqnarray}となります。これが $n^3$ となるときを考えると、まず、 $n^3$ の係数 $\dfrac{2a}{6}$ は $1$ でないといけないので、 $a=3$ がわかります。これを代入すると \begin{eqnarray} & & n \left\{\frac{3(2n^2+3n+1)}{6}+\frac{b(n+1)}{2}+(c-1) \right\} \\[5pt] &=& n \left\{\frac{6n^2+9n+3}{6}+\frac{b(n+1)}{2}+(c-1) \right\} \\[5pt] &=& n \left\{n^2 +\frac{3n+1}{2}+\frac{b(n+1)}{2}+(c-1) \right\} \\[5pt] \end{eqnarray}となります。 $n^2$ の係数 $\dfrac{3+b}{2}$ は $0$ でないといけないので、 $b=-3$ がわかります。これを代入すると \begin{eqnarray} & & n \left\{n^2 +\frac{3n+1}{2}+\frac{-3(n+1)}{2}+(c-1) \right\} \\[5pt] &=& n \left\{n^2 +\frac{3n+1}{2}+\frac{-3n-3}{2}+(c-1) \right\} \\[5pt] &=& n \left\{n^2 -1+(c-1) \right\} \\[5pt] \end{eqnarray}となります。 $n$ の係数 $-1+(c-1)$ は $0$ でないといけないので、 $c=2$ がわかります。代入すると、たしかに $n^3$ となります。

解答

シスセソ：3-32