共通テスト 数学II・数学B・数学C 2025年度 第3問 解説
【必答問題】
問題編
問題
$k$ を $0$ でない実数とし、$f(x)$ を $2$ 次関数とする。$F(x)$ と $G(x)$ はどちらも導関数が $f(x)$ であるような関数で、$F(x)$ は $x = 0$ で極小値 $0$ をとり、$G(x)$ は $x = k$ で極大値 $0$ をとるとする。
(1) まず、$F(x) = 2x^3 + 3x^2$ の場合を考える。
$F(x)$ の導関数が $f(x)$ であることから
\[ f(x) = \myBox{ア} x^2 + \myBox{イ} x \]であり、$F(x)$ は $x = \myBox{ウエ}$ で極大値をとる。また、$G(x)$ の導関数が $f(x)$ であることから
\[ G(x) = \myBox{オ} x^3 + \myBox{カ} x^2 + C \quad (C \text{ は積分定数}) \]と表され、$G(x)$ は $x = \myBox{キ}$ で極小値をとる。さらに $G(x)$ に関する条件から $C = \myBox{クケ}$ である。(2) 次に、$k \gt 0$ の場合を考える。
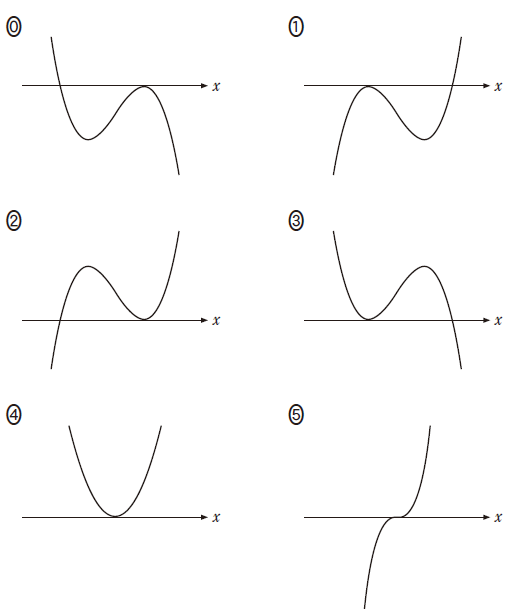
このとき、$F(x)$ と $G(x)$ に関する条件から、$y = F(x)$ のグラフと $F(x)$、 $G(x)$ の極値について調べよう。(i) $F(x)$ が $x = 0$ で極小値をとることから、$f(0) = \myBox{コ}$ であり、$x = 0$ の前後で $f(x)$ の符号は $\dBox{サ}$ 。さらに、$G(x)$ が $x = k$ で極大値をとることから、$f(k) = \myBox{シ}$ であり、$x = k$ の前後で $f(x)$ の符号は $\dBox{ス}$ 。したがって、$F(x)$ の導関数は $f(x)$ であることに注意すると、座標平面において $y = F(x)$ のグラフの概形は $\dBox{セ}$ であることがわかる。
$\dbox{サ},$ $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: 負から正に変わる
1: 正から負に変わる
2: 変わらない$\dbox{セ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。なお、$y$ 軸は省略しているが、上方向が正の方向であり、$x$ 軸は直線 $y = 0$ を表している。
(ii) $F(x)$ に関する条件から、すべての実数 $x$ に対して
\[ F(x) = \int_{\dBox{タ}}^{\dBox{ソ}} f(t) dt \]が成り立つ。このことと (i) の考察により、$F(x)$ の極大値は
\[ \int_{\dBox{ツ}}^{\dBox{チ}} f(t) dt \]と表され、$F(x)$ の極大値は、関数 $y = \dBox{テ}$ のグラフと $x$ 軸で囲まれた図形の $\dBox{ト}$ と等しいことがわかる。
さらに $G(x)$ に関する条件から、$F(x)$ の極大値は、$G(x)$ の $\dBox{ナ}$ と等しいことがわかる。$\dbox{ソ}$ ~ $\dbox{ツ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $k$
3: $x$$\dbox{テ}$ の解答群
0: $f(x)$
1: $F(x)$
2: $G(x)$$\dbox{ト}$ の解答群
0: 面積
1: 面積の $-1$ 倍$\dbox{ナ}$ の解答群
0: 極小値
1: 極大値
2: 極小値の $-1$ 倍
3: 極大値の $-1$ 倍
考え方
複雑な条件のように書かれていますが、 $F(x)$ と $G(x)$ の位置関係はシンプルです。後半は抽象的に書かれていますが、式の意味を考えれば計算なしで解答できます。全体的にほとんど計算はないです。
【必答問題】
解答編
問題
$k$ を $0$ でない実数とし、$f(x)$ を $2$ 次関数とする。$F(x)$ と $G(x)$ はどちらも導関数が $f(x)$ であるような関数で、$F(x)$ は $x = 0$ で極小値 $0$ をとり、$G(x)$ は $x = k$ で極大値 $0$ をとるとする。
(1) まず、$F(x) = 2x^3 + 3x^2$ の場合を考える。
$F(x)$ の導関数が $f(x)$ であることから
\[ f(x) = \myBox{ア} x^2 + \myBox{イ} x \]であり、$F(x)$ は $x = \myBox{ウエ}$ で極大値をとる。また、$G(x)$ の導関数が $f(x)$ であることから
\[ G(x) = \myBox{オ} x^3 + \myBox{カ} x^2 + C \quad (C \text{ は積分定数}) \]と表され、$G(x)$ は $x = \myBox{キ}$ で極小値をとる。さらに $G(x)$ に関する条件から $C = \myBox{クケ}$ である。
解説
(1) $F(x)=2x^3+3x^2$ を微分したものが $f(x)$ なので、\[ f(x)=6x^2+6x \]です。 $f(x)=6x(x+1)$ なので、 $F(x)=0$ となるのは、 $x=-1,0$ のときです。なので、増減表は次のようになります。
\begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 0 & \cdots \\
\hline
F'(x) & + & 0 & - & 0 & + \\
\hline
F(x) & \nearrow & & \searrow & & \nearrow &
\end{array}なので、 $F(x)$ は $x=-1$ のときに極大値をとることがわかります。
$G(x)$ を微分したものも $f(x)$ なので、\[ G(x)=2x^3+3x^2+C \]と書けます($C$ は積分定数)。増減表は先ほどと同じようにして次のようになることがわかります。
\begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 0 & \cdots \\
\hline
G'(x) & + & 0 & - & 0 & + \\
\hline
G(x) & \nearrow & & \searrow & & \nearrow &
\end{array}これより、 $x=0$ で極小値をとることがわかります。
問題文にある条件より、 $G(x)$ は $x=k$ で極大値 $0$ をとる、とあるので、 $x=-1$ を代入すると $0$ になることから
\begin{eqnarray}
G(-1) &=& 0 \\[5pt]
-2+3+C &=& 0 \\[5pt]
C &=& -1 \\[5pt]
\end{eqnarray}となります。
解答
アイ:66
ウエ:-1
オカ:23
キ:0
クケ:-1
解答編 つづき
問題
(2) 次に、$k \gt 0$ の場合を考える。
このとき、$F(x)$ と $G(x)$ に関する条件から、$y = F(x)$ のグラフと $F(x)$、 $G(x)$ の極値について調べよう。(i) $F(x)$ が $x = 0$ で極小値をとることから、$f(0) = \myBox{コ}$ であり、$x = 0$ の前後で $f(x)$ の符号は $\dBox{サ}$ 。さらに、$G(x)$ が $x = k$ で極大値をとることから、$f(k) = \myBox{シ}$ であり、$x = k$ の前後で $f(x)$ の符号は $\dBox{ス}$ 。したがって、$F(x)$ の導関数は $f(x)$ であることに注意すると、座標平面において $y = F(x)$ のグラフの概形は $\dBox{セ}$ であることがわかる。
$\dbox{サ},$ $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: 負から正に変わる
1: 正から負に変わる
2: 変わらない$\dbox{セ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。なお、$y$ 軸は省略しているが、上方向が正の方向であり、$x$ 軸は直線 $y = 0$ を表している。
解説
(2)(i)
$F(x)$ が $x=0$ で極小値をとるので、 $F'(0)=f(0)=0$ です。 $x=0$ の前後で、 $F'(x)=f(x)$ の符号は負から正にかわります((1)の増減表も参考になります)。
$G(x)$ が $x=k$ で極大値をとるから、 $G'(k)=f(k)=0$ です。 $x=k$ の前後で、 $G'(x)=f(x)$ の符号は正から負にかわります。
つまり、 $x=0$ のところで谷のようになっていて、 $x=k$ のところで山のようになっています。これを満たすのは、選択肢の中では 0 か 3 です。 $F(x)$ の極小値が $0$ だと冒頭に書かれているので、極小値が $x$ 軸上にある 3 が $y=F(x)$ のグラフとなります。
解答
コサ:00
シス:01
セ:3
解答編 つづき
問題
(ii) $F(x)$ に関する条件から、すべての実数 $x$ に対して
\[ F(x) = \int_{\dBox{タ}}^{\dBox{ソ}} f(t) dt \]が成り立つ。このことと (i) の考察により、$F(x)$ の極大値は
\[ \int_{\dBox{ツ}}^{\dBox{チ}} f(t) dt \]と表され、$F(x)$ の極大値は、関数 $y = \dBox{テ}$ のグラフと $x$ 軸で囲まれた図形の $\dBox{ト}$ と等しいことがわかる。
さらに $G(x)$ に関する条件から、$F(x)$ の極大値は、$G(x)$ の $\dBox{ナ}$ と等しいことがわかる。$\dbox{ソ}$ ~ $\dbox{ツ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $k$
3: $x$$\dbox{テ}$ の解答群
0: $f(x)$
1: $F(x)$
2: $G(x)$$\dbox{ト}$ の解答群
0: 面積
1: 面積の $-1$ 倍$\dbox{ナ}$ の解答群
0: 極小値
1: 極大値
2: 極小値の $-1$ 倍
3: 極大値の $-1$ 倍
解説
(2)(ii)
$F(x)$ を微分したものが $f(x)$ だから、 $f(x)$ を積分すると $F(x)$ になります。ある定数 $a$ から $x$ まで積分すると\[ \int_a^x f(t)dt =F(x)-F(a) \]となります。なので、 $a$ は $F(a)=0$ となるように選べばよく、 $a=0$ とすればいいことがわかります。セのグラフのように $F(a)=0$ となる $a$ はもう一つありますが、これは $k$ より大きい値であり、選択肢の中に該当するものはありません。
$G(x)$ は $x=k$ で極大値をとるので、 $f(x)$ の符号は正から負に変わります。そのため、 $F(x)$ も $x=k$ で極大値をとることがわかります。このことから、$F(x)$ の極大値は $F(k)$ なので、\[ \int_0^k f(t) dt \]と表すことができます。
$f(0)=f(k)=0$ であり、増減を考えると、グラフは セ ようになるため、 $0\lt x\lt k$ の部分は $x$ 軸より上にあるので、この極大値は、 $y=f(x)$ のグラフと $x$ 軸で囲まれた図形の面積と等しいことがわかります。
$G(x)$ も $F(x)$ も微分すると同じ関数 $f(x)$ になるので、グラフの形は同じで、上下にずれているだけです。 $G(k)=0$ なので、セ のグラフの選択肢でいうと、 0 に対応します。極大値の部分に着目すると、 $y=F(x)$ のグラフと $y=G(x)$ のグラフは、 $(k,F(k))$ と $(k,0)$ とが対応しているので、 $y=F(x)$ のグラフを $F(k)$ だけ下に移動したものが $y=G(x)$ のグラフとなっています。
極小値に着目すると、 $(0,0)$ が $(0,G(0))$ に移動しているため、 $G(x)$ の極小値は $-F(k)$ と等しいです。つまり、 $F(x)$ の極大値は、 $G(x)$ の極小値の $-1$ 倍だとわかります。
解答
ソタ:30
チツ:20
テト:00
ナ:2